10.1: Inversion

Let \(\Omega\) be the circle with center \(O\) and radius \(r\). The inversion of a point \(P\) in \(\Omega\) is the point \(P' \in [OP)\) such that

\(OP \cdot OP' = r^2.\)

In this case the circle \(\Omega\) will be called the circle of inversion and its center \(O\) is called the center of inversion.

The inverse of \(O\) is undefined.

Note that if \(P\) is inside \(\Omega\), then \(P'\) is outside and the other way around. Further, \(P = P'\) if and only if \(P \in \Omega\).

Note that the inversion maps \(P'\) back to \(P\).

Exercise \(\PageIndex{1}\)

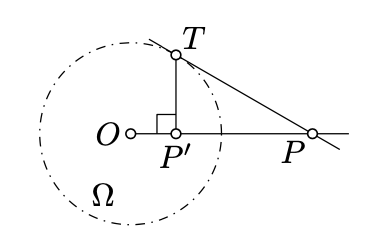
Let \(\Omega\) be a circle centered at \(O\). Suppose that a line \((PT)\) is tangent to \(\Omega\) at \(T\). Let \(P'\) be the foot point of \(T\) on \((OP)\).

Show that \(P'\) is the inverse of \(P\) in \(\Omega\).

Hint

By Lemma 5.6.2, \(\angle OTP'\) is right. Therefore, \(\triangle OPT \sim \triangle OTP'\) and in particular \(OP \cdot OP' = OT^2\) and hence the result.

Lemma \(\PageIndex{1}\)

Let \(\Gamma\) be a circle with the center \(O\). Assume \(A'\) and \(B'\) are the inverses of \(A\) and \(B\) in \(\Gamma\). Then

\(\triangle OAB \sim \triangle OB'A'.\)

Moreover

\[\begin{array} {rcl} {\measuredangle AOB} & \equiv & {-\measuredangle B'OA',} \\ {\measuredangle OBA} & \equiv & {-\measuredangle OA'B',} \\ {\measuredangle BAO} & \equiv & {-\measuredangle A'B'O.} \end{array}\]

Proof

Let \(r\) be the radius of the circle of the inversion.

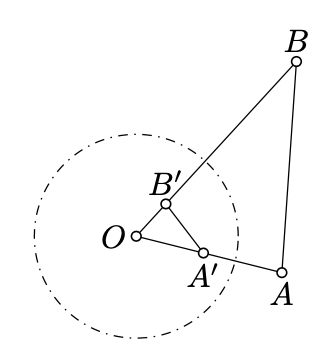
By the definition of inversion,

\(OA \cdot OA' = OB \cdot OB' = r^2.\)

Therefore,

\(\dfrac{OA}{OB'} = \dfrac{OB}{OA'}.\)

Clearly,

\(\measuredangle AOB = \measuredangle A'OB' \equiv -\measuredangle B'OA'.\)

From SAS, we get that

\(\triangle OAB \sim \triangle OB'A'.\)

Applying Theorem 3.3.1 and 10.1.2, we get 10.1.1.

Exercise \(\PageIndex{2}\)

Let \(P'\) be the inverse of \(P\) in the circle \(\Gamma\). Assume that \(P \ne P'\). Show that the value \(\dfrac{PX}{P'X}\) is the same for all \(X \in \Gamma\).

The converse to the exercise above also holds. Namely, given a positive real number \(k \ne 1\) and two distinct points \(P\) and \(P'\) the locus of points \(X\) such that \(\dfrac{PX}{P'X} = k\) forms a circle which is called the Apollonian circle. In this case \(P'\) is inverse of \(P\) in the Apollonian circle.

Hint

Suppose that \(O\) denotes the center of \(\Gamma\). Assume that \(X, Y \in \Gamma\); in particular, \(OX = OY\).

Note that the inversion sends \(X\) and \(Y\) to themselves. By Lemma \(\PageIndex{1}\),

\(\triangle OPX \sim \triangle OXP'\) and \(\triangle OPY \sim \triangle OYP'\).

Therefore, \(\dfrac{PX}{P'X} = \dfrac{OP}{OX} = \dfrac{OP}{OY} = \dfrac{PY}{P'Y}\) and hence the result.

Exercise \(\PageIndex{3}\)

Let \(A',B'\), and \(C'\) be the images of \(A,B\), and \(C\) under the inversion in the cincircle of \(\triangle ABC\). Show that the incenter of \(\triangle ABC\) is the orthocenter of \(\triangle A'B'C'\).

Hint

By Lemma \(\PageIndex{1}\),

\(\measuredangle IA'B' \equiv -\measuredangle IBA\), \(\measuredangle IB'C' \equiv -\measuredangle ICB\), \(\measuredangle IC'A' \equiv -\measuredangle IAC\),
\(\measuredangle IB'A' \equiv -\measuredangle IAB\), \(\measuredangle IC'B' \equiv -\measuredangle IBC\), \(\measuredangle IA'C' \equiv -\measuredangle ICA\).

It remains to apply the theorem on the sum of angles of triangle (Theorem 7.4.1) to show that \((A'I) \perp (B'C')\), \((B'I) \perp (C'A')\) and \((C'I) \perp (B'A')\).

Exercise \(\PageIndex{4}\)

Make a ruler-and-compass construction of the inverse of a given point in a given circle.

Hint

Guess the construction from the diagram (the two nonintersecting lines on the diagram are parallel).