12.4: Axiom I

Evidently, the h-plane contains at least two points. Therefore, to show that Axiom I holds in the h-plane, we need to show that the h-distance defined in 12.1 is a metric on h-plane; that is, the conditions (a) - (d) in Definition 1.3.1 hold for h-distance.

The following claim says that the h-distance meets the conditions (a) and (b)

Claim $\PageIndex{1}$

Given the h-points $P$ and $Q$, we have $PQ_h \ge 0$ and $PQ_h=0$ if and only if $P=Q$.

Proof

According to Lemma 12.3.1 and the main observation (Theorem 12.3.1), we may assume that $Q$ is the center of the absolute. In this case

and therefore

Moreover, the equalities holds if and only if $P=Q$.

The following claim says that the h-distance meets the condition

Claim $\PageIndex{2}$

For any h-points $P$ and $Q$, we have $PQ_h=QP_h$.

Proof

Let $A$ and $B$ be ideal points of $(PQ)_h$ and $A,P,Q,B$ appear on the circline containing $(PQ)_h$ in the same order.

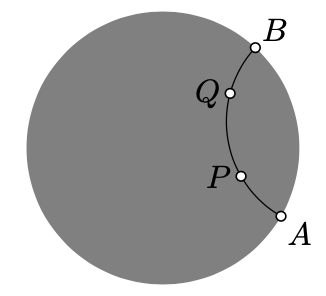
Then

$\begin{array} {rcl} {PQ_h} & = & {\ln \dfrac{AQ \cdot BP}{QB \cdot PA} =} \\ {} & = & {=\ln \dfrac{BP \cdot AQ}{PA \cdot QB}=} \\ {} & = & {QP_h} \end{array}$

The following claim shows, in particular, that the triangle inequality (which is Definition 1.3.1d) holds for $h$-distance.

Claim $\PageIndex{3}$

Given a triple of h-points $P$, $Q$, and $R$, we have

Moreover, the equality holds if and only if $P$, $Q$, and $R$ lie on one h-line in the same order.

Proof

Without loss of generality, we may assume that $P$ is the center of the absolute and $PQ_h \ge QR_h >0$.

Suppose that $\Delta$ denotes the h-circle with the center $Q$ and h-radius $\rho=QR_h$. Let $S$ and $T$ be the points of intersection of $(PQ)$ and $\Delta$.

By Lemma 12.3.3, $PQ_h\z\ge QR_h$. Therefore, we can assume that the points $P$, $S$, $Q$, and $T$ appear on the h-line in the same order.

According to Lemma Lemma 12.3.4, $\Delta$ is a Euclidean circle; suppose that $\hat Q$ denotes its Euclidean center. Note that $\hat Q$ is the Euclidean midpoint of $[ST]$.

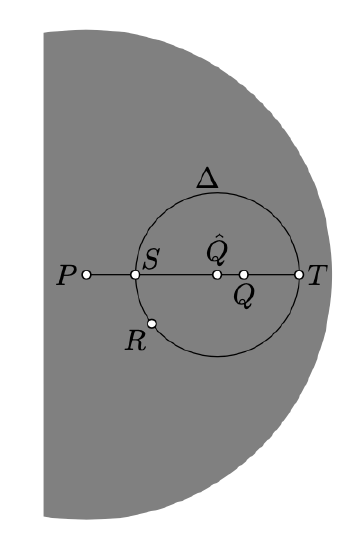
By the Euclidean triangle inequality

$$PT = P\hat{Q}+\hat{Q} R \ge PR$$

and the equality holds if and only if $T=R$.

By Lemma Lemma 12.3.2,

$\begin{array} {l} {PT_h = \ln \dfrac{1 + PT}{1 - PT},} \\ {PR_h = \ln \dfrac{1 + PR}{1 - PR}.} \end{array}$

Since the function $f(x)=\ln\frac{1+x}{1-x}$ is increasing for $x\in[0,1)$, inequality 12.4.1 implies

$PT_h\ge PR_h$

and the equality holds if and only if $T=R$.

Finally, applying Lemma 12.3.3 again, we get that

$PT_h=PQ_h+QR_h.$

Hence the claim follows.