2.1: Elementary Neutral Geometry
( \newcommand{\kernel}{\mathrm{null}\,}\)
Most of the following results date from antiquity but, even if so, we will consistently use modern language and you should too. In addition, try to be careful with symbolism. It is too hard for me to do that in my word processor but always add distinguishing symbols as appropriate - Do as I say, not as I do! For example, the line segment ¯AB should be written with a bar over it, ray ¯AB with an arrow, the same ray could be indicated by writing BA with the arrow reversed (that my word processor can’t do), and line →AB with a double-headed arrow. Note that line segment ¯AB is equal to line segment ¯BA as sets. That is, they are one and the same set but rays →AB and →BA are not the same set. Formally:
segment ¯AB={X∣X∈→AB with X=A,X=B, or X between A and B}, and ray AB={X∣X∈→AB with X=A,X=B,X between A and B, or B between A and X}.
Does "between" make sense? It had better! This is yet another example of our semi-formality.
Using these conventions consistently "frees up" the use of AB with no symbolic modifiers to indicate the measure of line segment ¯AB; i.e., the distance from A to B,m(¯AB), can be simplified as AB.
Although congruence is an undefined term in a strictly formal geometry, our axioms always have a concept of length of a line segment (the Ruler Postulate) and angle measure (the Protractor Postulate) and, with those, the idea we want can be (and is!) defined as a one-to-one correspondence that preserves the distance between any two points and the measure of any two corresponding angles. [Note: "Distance preserving" makes the "one-to-one" redundant.] Any set is congruent to itself in the abstract but to say ¯AB≅¯BA is to assert more than its set equality; it implies such a distance-preserving correspondence but in reverse order. That is, A is "mapped to" B, the point 1/3 of the way from A to B to the point 1/3 of the way from B to A, etc.; i.e., all other points likewise. It is true although we won’t worry about such things unless nagged but, for completeness sake, it is the reflection of the segment in its perpendicular bisector. Similarly, ∠ABC≅∠CBA is true but not just because they are one and the same set; i.e., not because of the "reflexive property of congruence" (although you will see that in many elementary geometry books!). Again there is an underlying congruence, namely, the reflection of the angle in the line that bisects the angle.
In fact, it is even deeper than a distance and angle preserving correspondence between the two sets. To be formal about it, a congruence is defined to be a one-to-one, distance preserving, angle preserving correspondence from the entire point set of the geometry onto itself. That is, the assertion that two figures are congruent is an assertion that the entire point set can be matched to itself in a way that preserves all distances and angles as it "carries" one figure onto the other. In Euclidean plane geometry, a translation (glide or slide, in some elementary books), a rotation about a fixed point, and a reflection across a fixed line are all congruences, as well as compositions thereof. Are there others? Are these congruences of so-called "neutral" geometry as well? The answers are no, yes, and yes but we won’t worry about it until Chapter 5 although some presentations are built around it. We still have not proved last of the congruence theorems:
Two right triangles with hypotenuses congruent and one pair of legs congruent are congruent. Restated specifically:
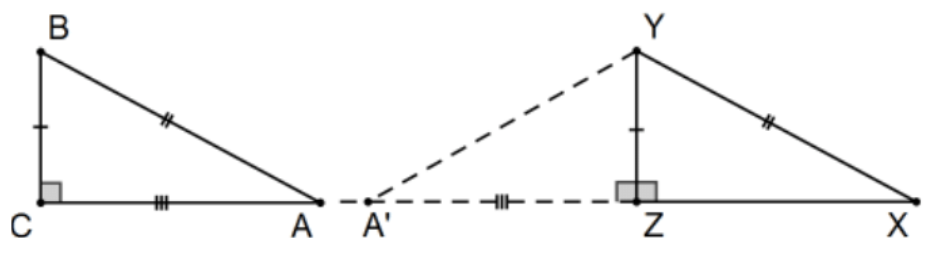
Given: △ABC and △XYZ with ∠C and ∠Z right angles, AB≅XY, and BC≅YZ
Prove: △ABC≅△XYZ
Proof: Take A′ along ray XZ with ZA′≅CA. Then △A′YZ≅△ABC by SAS so A′Y≅AB and , by transitivity, A′Y≅XY so △A′YX is isosceles. Then ∠A′≅∠X but ∠A′≅∠A by cpctc so △A′YZ≅△XYZ by AAS (in a couple of different ways). Finally, △ABC≅△XYZ by transitivity. QED.
Select any three points on the given circle and construct the perpendicular bisectors of any two of the three chords they determine. These do intersect and their point of intersection is the center of the circle.
Proof: (PS 1, #21) Know it, its proof, and lots of other easy ones.
Note 1: Why not all three pairs? Hint: It is not wrong but makes the proof much harder. Why?
Note 2: This does not prove that any triangle has a circumcircle because it does not prove that the perpendicular bisectors of two of its sides intersect. If they do intersect, then all 3 vertices of the triangle are equidistant from that point of intersection and the set of all points equidistant from that point is a circle that contains the 3 vertices, hence the circumcircle, and the intersection point is its center, called the circumcenter of the triangle. Note that this point is equidistant from each pair of points on the circle and hence on its perpendicular bisector so all such perpendicular bisectors are concurrent. In our case, the three points were already on a circle so, obviously, its center must lie on each of the two perpendicular bisectors. Therefore they must intersect to identify the center. QED.
Theorem: Tangent iff Perpendicular to Radius: A line that intersects a circle at a point is tangent to the circle at that point iff it is perpendicular to the radius to that point of intersection.
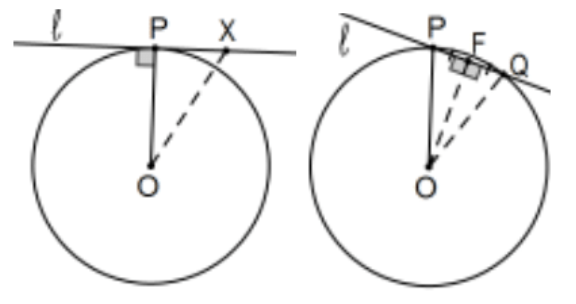
Proof: First the "if", suppose P is on circle O and the given line ℓ is perpendicular to radius OP. Let X be any point on the line other than P. Then △OPX is a right triangle with hypotenuse OX>OP that forces X to be outside the circle so only one point of intersection of line ℓ and circle O. By definition of tangent, the line is tangent to the circle at that point. Conversely, assume line ℓ is tangent to circle O and let F be the foot of the perpendicular from O to the line. If it were true that F≠P, let Q be the point on the opposite side of F with the FQ≅FP. Then △OFQ≅△OFP, by SAS, so OQ≅OP and Q would be a second point of line ℓ on circle O and the line is not tangent since Q≠P. This proves the inverse (if not perpendicular, then not tangent), not the converse as expected, but they are logically equivalent. QED.
Theorem: To Construct the Incircle of a Triangle:
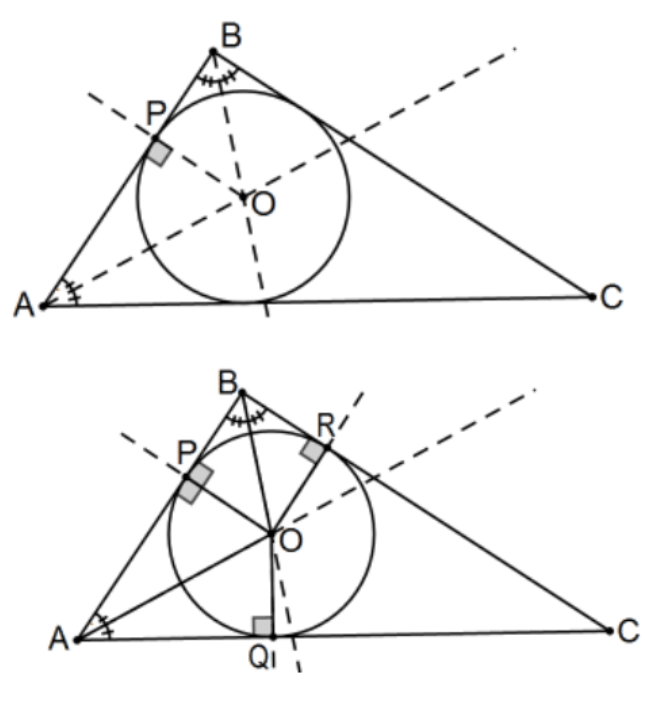
Construction: Construct the bisectors of two of the angles of the triangle. The unspecified(!) axioms do guarantee that they intersect (since they are inside the closed and bounded triangle). That point is the incenter of the triangle. To determine the radius, construct the perpendicular to any one of its sides. With the center and the radius constructed, the circle is constructed.
Proof: Let Q and R be the perpendiculars to the other two sides where O was determined by the bisectors of angles A and B. △AOP≅△AOQ and △BOP≅△BOR by AAS so that OP≅OQ≅OR. That implies that P,Q, and R lie on the circle with center at O and radius OP. The perpendicularity of the radii with each of the sides implies that this circle is tangent to each of the sides, the incircle.
Corollary: The angle bisectors of a triangle are concurrent.
Proof: Just prove that the ray (already determined) from the third vertex C through the incenter O in the proof of the theorem above bisects that third angle. [Hint: Use Hypotenuse-Leg.] QED.
Note: This approach to proving that entities that share some common description share some other common description is important: Quit "constructing" as soon as the needed entity is determined and prove everything else about it. If not, the proof is made much more difficult by having to show that apparently different entities are really one and the same. That is, O was determined by bisecting two of the angles. Bisecting the third angle would (ostensibly) determine two more points that would have to be shown to be the same point. Avoid the problem by never "overdetermining" anything. Stop saying "let x be" when x is determined and prove everything appropriate about it. As another example from the construction, the second and third perpendiculars were not part of the actual construction, only part of the proof of validity.
Theorem: Angle Sum Theorem (neutral geometry form): The sum of the angles of a triangle is not greater than two right angles. [So for an n-gon, not greater than 180(n−2).]
Proof: One nice proof is an extension of the previous proof of the Exterior Angle Theorem but first we consider some preliminary ideas.
[Note: We are no longer in our literal "real world"; i.e., life on a sphere. Here there are no parallel lines (any two lines intersect in antipodal points; i.e., the midpoint of the Euclidean segment they determine is the center of the sphere). Consider a triangle determined by two longitudinal line segments from the North Pole to the Equator and the segment of the Equator that they determine. The angle sum of such a triangle is 90∘+ 90∘+x∘ where x∘ is the measure of the angle at the North Pole. What is wrong in the proof; something must be?! Hint: Size matters on a sphere. What is "too big"? See PS 2, #27.]
Definition: Two polygons are equivalent if one can be cut up into a finite number of polygons and the pieces rearranged to make the other; i.e., to fit perfectly. [A formal definition of this is tricky, so we won’t bother!] Example: Snip a 2×8 rectangle in the middle and rearrange to obtain a 4×4 square.
Question? What is a rectangle? Are there any? Answer: Yes (in Euclidean geometry) or No (hyperbolic).
Note: Area hasn’t been defined but, whatever it might be, it should be the same for equivalent figures!
Theorem: If two triangles are equivalent, then they have the same angle sum. More generally, if a triangle is equivalent to an n-gon the difference of their angle sums is 180(n−3).
Proof: Handwaving. We’re not supposed to do that in mathematics but a formal proof would get in the road and would not be helpful. The idea is that vertices introduced by the cutting will either be in the interior where the constituent angles add to 360∘ or along an edge where they add to 180∘. As these pieces are rearranged, the perfect fit requires the same situation. A formal proof would be by some kind of tricky mathematical induction. Fortunately, we do not need the full power of this result to complete the proof of the Angle Sum Theorem; we can prove what we need as we go along:
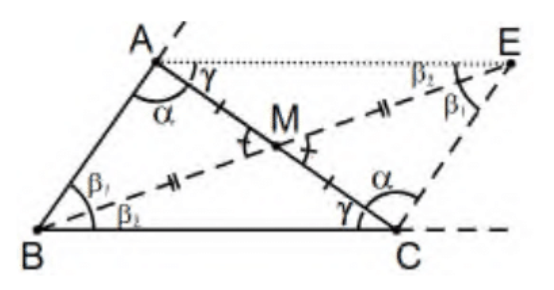
In the proof of the Exterior Angle Theorem, Prop 16, it is easy to see that △EBC is equivalent to the original △ABC. In the process, ∠B was divided into two angles and that each subangle is involved in this new triangle, ∠EBC is one of those angles and ∠EBA≅∠BEC is the other. Moreover, ∠A is congruent to ∠ECM that is a component part of ∠BCE with the original ∠C being the rest of ∠BCE. Therefore, the angle sum of this new △EBC is the same as the original △ABC. If, as usual, we take m(∠B)=β and take the measures of the two subdivided angles as β=β1+β2 as indicated, at least one of β1 or β2 must be less than or equal to β/2 because, if both were greater than β/2, their sum would exceed β, an impossibility. In our figure, the smaller appears to be β2, in which case, we would proceed with Δ EBC as pictured but it were to be β1, we would use △EBA, also pictured and also equivalent to ΔABC and where all of the same remarks apply.
Finally, we are ready to begin an indirect proof; i.e., assume this △ABC is one with angle sum greater than 180∘. Express this "excess" by ε>0. In other words, α+β+γ=180+ε. The new triangle, ΔEBC has the same angle sum but with the new angle at B of measure less than or equal to β/2=β/21.
Repeating the same construction (i.e., with the median of B through the midpoint of side CE, we obtain a triangle with the same angle sum but, this time, the measure of the angle at B is less than or equal to β/22, and repeating n times, β/2n where, for sufficiently large n,β/2n<ε. So what? By Prop 17 , the other two angles have a sum, say x, of less than 180∘ so adding in the angle at B, say y, we have a triangle with angle sum of 180+ε=x+y with x<180 and y<ε. Obviously, this cannot be so; there is no such triangle and the angle sum of any triangle does not exceed 180∘. QED.
Corollary: If a line intersects two sides of a rectangle it divides it into two polygons with no "deficit"; i.e., their angle sums less can’t be than they "should be". For example, if one of the polygons is a right triangle, then the other two angles are complementary or, if it’s a quadrilateral, the two adjacent angles not known to be right angles are supplementary. The idea is that if either resulting n-gon has angle sum strictly less than 180∘(n−2), then ... [But, again, are there any rectangles? Wait till the next chapter.]
Corollary: The opposite sides of a rectangle are congruent. [Note: This was a corollary to PS 1, #23.] Moreover, it is not a theorem about parallelograms in general.]
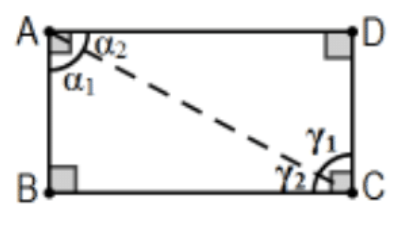
Proof: Either diagonal of a rectangle divides it into two right triangles. There can be no "deficit", the angle sum of each must be 180∘, since the two acute angles of each compose a right angle of the rectangle. Specifically with reference to the pictured rectangle, each vertex angle is a right angle so that α1+α2=γ1+γ2=90∘ and, since each triangle has angle sum less than or equal 180∘,α1+γ2≤90∘ and α2+γ1≤90∘. If either of these inequalities were strict (i.e., <), we would have (α1+γ2)+(α2+γ1)<180∘ and, rearranging the terms, 180∘=(α1+α2)+(γ1+γ2)<180∘. This contradiction forces both α1+γ2=90∘ and α2+γ1=90∘. That is, α1=90∘−γ2=γ1 and α2=90∘−γ1=γ2. Either equation alone, along with right angles at B and D and the common diagonal, imply that △ACD≅△CAB by AAS or, using them both, by ASA. In either case, by cpctc, the opposite sides are congruent.
Theorem: ASA for Long Triangles. First off, there is no such thing; i.e., a "long triangle" is not a triangle at all. It is a convenient name for a figure that is the union of two rays that, together with the segment of their initial points, do not intersect. [Note: This name is not used universally in geometry.]
[Note: This was a definition; you need to know definitions even if never written down!] The theorem? Effectively, if ABCD and EFGH are geometric figures such that ∠B≅∠F,∠C≅∠G, and segments BC≅FG, then rays BA and CD intersect iff rays FE and GH intersect. [Equivalently, one pair does not intersect iff the other pair does not intersect; i.e., one is "long" iff the other is.]
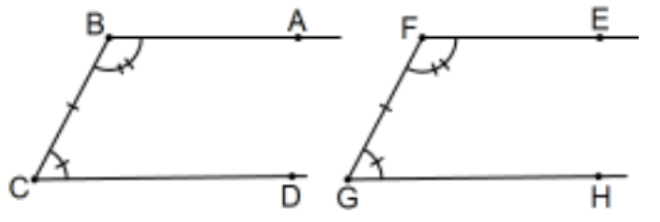
Proof: Suppose rays BA and CD do intersect, say at X, and take Y along GH with GY≅CX. Then △BCX≅△FGY by SAS and ∠CBX≅∠GFY by cpctc. But ∠CBX=∠CBA=∠B (i.e., one and the same angle) so, by hypothesis and the Protractor Postulate, Y is also on ray FE, the point of intersection with ray GH. QED.
Note: These long triangles are "congruent"; i.e., there is a one-to-one correspondence such that all distances and angles are preserved) and this proof could be cleaned up to accommodate it. We won’t need it.
Definition: A Saccheri quadrilateral is a quadrilateral with one pair of opposite sides, called legs, that are congruent and perpendicular to (on the same side of) the line of its base. Its fourth side is called its summit. For example, Fig. ABCD is a Saccheri quadrilateral since lines AB and CD are perpendicular to line BC and segments AB≅DC. In this case, these segments are the legs, segment BC is the base, and segment AD is the summit. Line AD is the summit line.
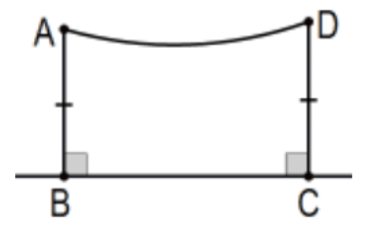
Theorem: The summit angles of a Saccheri quadrilateral are congruent (and therefore not obtuse).
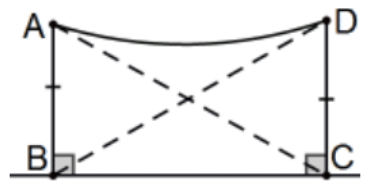
Proof 1: Know several and be able to correctly finish any prompt I might give. Probably the most obvious proof uses the diagonals AC and BD as indicated. Obviously, △ABC≅△DCB by SAS so that AC≅DB and △ABD≅△DCA by SSS so that the original ∠A≅∠D by cpctc. QED.
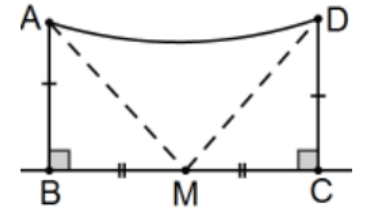
Proof 2: A less obvious but still easy proof is using exactly one auxiliary point, the midpoint M of the base BC as pictured. Obviously, △ABM≅△DCM by SAS so that AM≅DM and △AMD is isosceles so its base angles are congruent by previous theorem. Combined with the other pair of congruent angles at A and D (by cpctc), we have another proof that the summit angles are congruent. QED.
Note 1: As a matter of good form in a situation such as in that second proof, do say something like, "Let M be the midpoint of line segment BC." but don’t say anything about "let" or "construct" anything else. At that point, segment AM, ray AM, and other such that may be needed already exist. Just use them.
Note 2: A Saccheri quadrilateral need not (at least not yet proved) be a rectangle. In Euclidean geometry, they turn out to be one and the same but in neutral geometry, the summit angles may or may not be right angles. What is a rectangle? [Hint: Clear your throat while saying "right" as if you were Olde Englisch.]
Theorem: In a Saccheri quadrilateral, these are the same line:
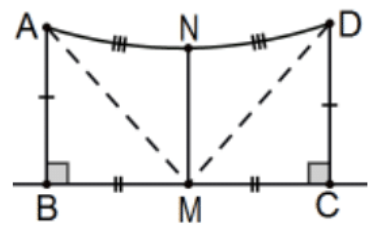
i. The line of the midpoints of the base and the summit.
ii. The perpendicular bisector of the base.
iii. The perpendicular bisector of the summit.
Proof: See PS 2, #12-16. For i implies ii and iii:
Let M be the midpoint of the base and N the midpoint of the summit of the Saccheri quadrilateral ABCD as pictured. Then △ABM≅△DCM by SAS so AM≅DM by cpctc and △AMN≅△DMN by SSS. Finally, the angles at N are both congruent (cpctc) and supplementary hence line MN is perpendicular to the summit and, by adding pairs of congruent angles, it is also perpendicular to the base. Since it was given that it bisected each (i.e., "let"), the line is the perpendicular bisector of each. QED
Note: The (lines of) the base and summit of a Saccheri quadrilateral share a common perpendicular. Therefore, among other things, they are parallel by the EAT. Another result of this proof is that it provides more proofs of the preceding theorem; the summit angles of a Saccheri quadrilateral are congruent.
Theorem: [Associated Saccheri Quadrilateral] In a triangle, consider the line determined by the midpoints of two sides and the perpendiculars to that line from the two vertices on the same side of that line. The segments determined form a Saccheri quadrilateral that is equivalent to the original triangle with summit angles such that their sum is the sum of the interior angles of the triangle.
[What are its base, legs, and summit?]
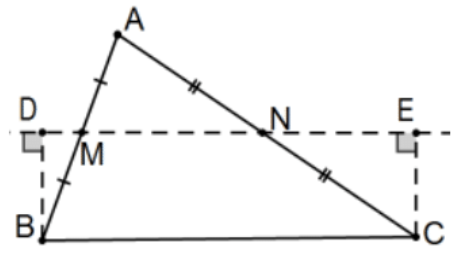
Construction: Know it. In △ABC, let M and N be the midpoints of two of its sides; in the pictured case, segments AB and AC, respectively. Let D and E be the feet of the lines perpendicular to line MN from the two vertices of △ABC on the same side of line MN; in this case, vertices B and C. Then BDEC is the desired Saccheri quadrilateral with summit BC.
Note: This is the construction of only one of the three associated quadrilaterals of △ABC; there is another with summit AB and a third with summit AC.
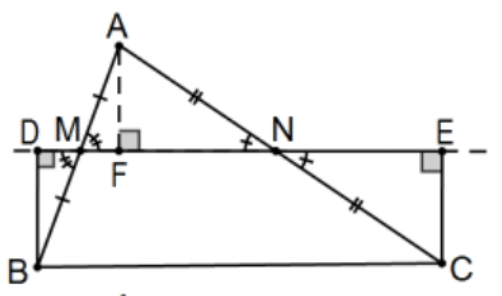
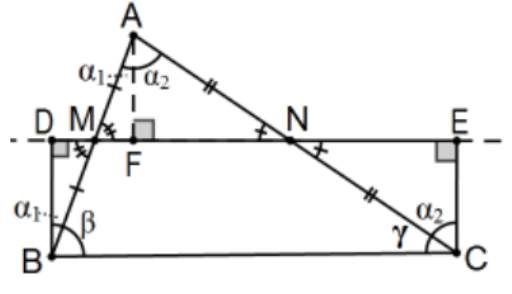
Proof: The most natural proof uses AAS by dropping the perpendicular from A to DE to determine F and conclude that BD≅AF≅CE so that BD≅CE, the only detail needed to conclude BDEC is Saccheri and the equivalence of that quadrilateral with △ABC is obvious.
[Note: There is an alternate proof that uses SAS. See PS 2, #23.]
However, the proof is not complete because we haven’t discussed angle sums. Moreover, even the rest of the proof is not complete because it implicitly assumes that F falls between M and N and that need not be the case. Continuing with that assumption, the angle sum conclusion is easy. Starting with the summit angles, we compute:
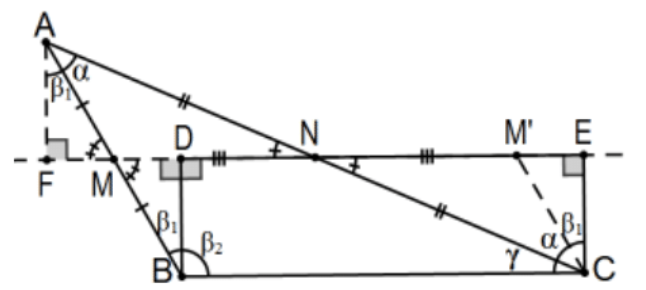
(α1+β)+(γ+α2)=(α1+α2)+β+γ=α+β+γ as required. Although the proof above is not valid if ∠B is obtuse, the result it is still true. In the indicated figure, let M′ be the point along ray NE such that segments NM′≅NM. Now △ANM≅△CNM′ by SAS so that M′C≅MA and, by supplementation, ∠CM′E≅∠AMF so that ΔCM′E≅△AMF≅△BMD by AAS.
This time β=β1+β2 and, again starting with the summit angles:
β2+(γ+α+β1)=α+(β1+β2)+γ=α+β+γ QED.
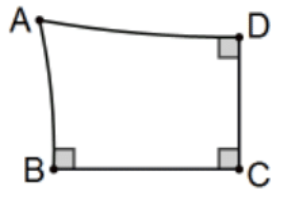
A Lambert quadrilateral is a quadrilateral with three right angles. [In Fig. ABCD, angles B,C, and D are right angles. What is the size of ∠A?]
In a Saccheri quadrilateral, the line determined by the midpoints of the base and the summit determine two congruent Lambert quadrilaterals.
Proof: It’s done already except for the formal meaning of congruent polygons. [That is, a distance preserving, angle preserving transformation of the entire plane. Reflection in that line of midpoints provides the needed congruence function. QED.
Each side of the fourth angle of a Lambert quadrilateral is greater than or equal to (i.e., not shorter than) the side opposite it and its 4th angle is not obtuse.
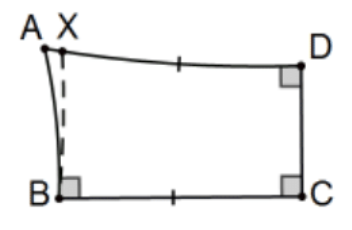
Proof: Suppose ABCD is the Lambert quadrilateral with unknown angle A. Let X be along ray DA with segment DX congruent to segment CB. Then figure BCDX is a Saccheri quadrilateral with summit BX. ∠XBC≤∠ABC so DX ≤ DA (why?). QED.
The summit of a Saccheri quadrilateral is greater than or equal to its base and its summit angles are not obtuse.
Proof: These are immediate corollaries to the above (but start with a Saccheri quad, not a Lambert.)
These quadrilaterals (both "almost" rectangles) were studied extensively by their eponyms in an effort to prove Euclid’s 5th Postulate. As is indicated in this last theorem, anything provable by one approach can be translated into a proof of the other. The trick is in being careful to start where you need to start. For example, in the above, start with a general Saccheri quadrilateral; do not start with a Lambert quadrilateral. Another example is that the fourth angle of a Lambert quadrilateral is not obtuse. This time to prove it, start with a general Lambert quadrilateral and construct a useful Saccheri quadrilateral.
There are other theorems of neutral geometry that could be proved, especially ones that can be stated in this "greater than or equal to" form but will be stated only in their hyperbolic geometry "strict" form in the next chapter. We will break here and start looking at them from that perspective.


