2.2: Problem Set 2

Exs 1-6 relate to the pictured lines \(\ell\) and \(m\) that share a transversal that forms a pair of congruent alternate interior angles, \(\angle B A C \cong \angle A B D\). In each case, let \(\mathrm{M}\) be the midpoint of segment \(\mathrm{AB}\) and let \(\mathrm{E}\) be the foot of the perpendicular from \(\mathrm{M}\) to \(\ell\). Moreover, start by making a corresponding sketch all given information in the standard manner and, equally important, nothing but the given information. Then prove the resulting line EF is a common perpendicular of the two lines freely using any of the standard congruence statements SAS, SSS, ASA, AAS, or Hypotenuse-Leg as appropriate. [Assume that line AB is not perpendicular to line \(\ell\) or we’re already done!]

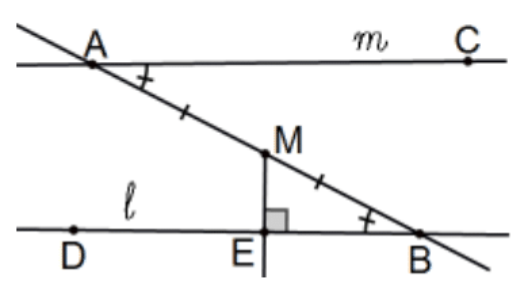
1. Let \(\mathbf{F}\) be the intersection of line EM with \(m\). [Assuming that they DO intersect!]
2. Let \(\mathrm{F}\) be the foot of the perpendicular from \(\mathrm{M}\) to \(m\).

[Note: Don’t forget to show that E, M, and F are collinear.]

3. Let \(\mathrm{F}\) be the foot of the perpendicular from A to line EM.

4. Let \(\mathrm{F}\) be the point along ray \(\mathrm{AC}\) with \(\mathrm{AF} \cong \mathrm{BE}\).
5. Let \(\mathrm{F}\) be the point along ray \(\mathrm{EM}\) with \(\mathrm{MF} \cong \mathrm{ME}\).
6. Let \(\mathrm{F}\) be the (correct) intersection of circles (A; BE) and (M; ME); i.e., the circles centered at A of radius \(\mathrm{BE}\) and at \(\mathrm{M}\) of radius ME.

Note: It is preferable to use fewer symbols but well-chosen words in stating mathematical results; it focuses more on the concepts instead of their specific presentation. Exs. 7-10 repeat four of Exs 1-6 exhibiting that philosophy.

7. Use SAS to prove that if a transversal to two lines forms a pair of congruent alternate interior angles, then the lines have a common perpendicular.

8. Use ASA to prove that if a transversal to two lines forms a pair of congruent alternate interior angles, then the lines have a common perpendicular.
9. Use AAS to prove that if a transversal to two lines forms a pair of congruent alternate interior angles, then the lines have a common perpendicular.
10. Use SSS to prove that if a transversal to two lines forms a pair of congruent alternate interior angles, then the lines have a common perpendicular.
11. (In a sense, the converse of each of these 1-10) Prove that if a line is a common perpendicular to two other lines, any transversal to the lines that passes through the midpoint of the segment determined by the common perpendicular forms congruent alternate interior angles.

In Exs 12-16, assume \(\mathrm{ABCD}\) to be a Saccheri quadrilateral with summit \(\mathrm{AD}\) and prove that line MN is the perpendicular bisector of both the base and the summit where the new figure is determined by the information given in each exercise. Include an appropriate, competent sketch for each with all of the given information indicated as well as auxiliary points and segments you use but do not indicate any information about them that has to be proved.

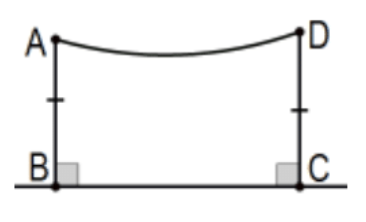
12. \(M\) and \(N\) are the midpoints of the base and summit, respectively, of ABCD.

13. \(M\) is the midpoint of the base of \(A B C D\) and \(N\) is determined by the perpendicular at \(M .\) [Verbally, the perpendicular bisector of the base is also the perpendicular bisector of the summit.]
14. \(\mathrm{N}\) is the midpoint of the summit of \(\mathrm{ABCD}\) and \(\mathrm{M}\) is determined by the perpendicular at \(\mathrm{N}\). [Verbally, the perpendicular bisector of the summit is also the perpendicular bisector of the base.]
15. \(\mathrm{N}\) is the midpoint of the summit of \(\mathrm{ABCD}\) and \(\mathrm{M}\) is the foot of the perpendicular at \(\mathrm{N}\) to the base.
16. \(M\) is the midpoint of the base of \(A B C D\) and \(N\) is the foot of the perpendicular at \(M\) to the summit.

In Exs 17-21, assume ABCD is a Lambert quadrilateral with fourth angle at \(A\) and prove that ABEF is a Saccheri quadrilateral with summit line AD where the new figure is determined by the information given in each exercise. Include an appropriate, competent sketch for each with all of the given information indicated and no other information indicated as given.

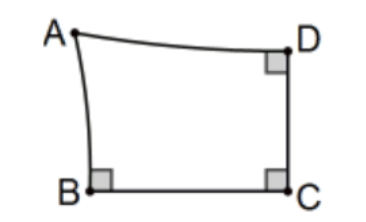
17. \(\mathrm{E}\) is along ray \(\mathrm{BC}\) with \(\mathrm{CE} \cong \mathrm{BC}\) and \(\mathrm{F}\) is along ray \(\mathrm{AD}\) with \(\mathrm{DF} \cong \mathrm{AD}\). [Informally, double each of a pair of of opposite sides.]

18. \(\mathrm{E}\) is along ray \(\mathrm{BC}\) with \(\mathrm{CE} \cong \mathrm{BC}\) and \(\mathrm{F}\) is on the perpendicular ray at \(\mathrm{E}\) with \(\mathrm{EF} \cong \mathrm{BA}\).
19. \(\mathrm{F}\) is along ray \(\mathrm{AD}\) with \(\mathrm{DF} \cong \mathrm{AD}\) and \(\mathrm{E}\) is the foot of the perpendicular at \(\mathrm{F}\) to line \(\mathrm{BC}\).
20. E is along ray \(\mathrm{BC}\) with \(\mathrm{CE} \cong \mathrm{BC}\) and \(\mathrm{F}\) is the intersection of \((\mathrm{E} ; \mathrm{AB})\), the circle centered at \(\mathrm{E}\) of radius \(\mathrm{AB}\) and \((\mathrm{D} ; \mathrm{AD})\), the circle centered at \(\mathrm{D}\) of radius AD. [Hint: Need to show TWO right angles.]
21. \(\mathrm{F}\) is along ray \(\mathrm{AD}\) with \(\mathrm{DF} \cong \mathrm{AD}\) and \(\mathrm{E}\) is the intersection of \((\mathrm{F} ; \mathrm{AB})\), the circle centered at \(\mathrm{F}\) of radius \(A B\), and \((C ; B C)\), the circle centered at \(C\) of radius \(B C\). [Hint: Need to show TWO right angles.]
22. \(\mathrm{E}\) is along ray \(\mathrm{BC}\) with \(\mathrm{CE} \cong \mathrm{BC}\) and \(\mathrm{F}\) is the intersection of the perpendicular at \(\mathrm{E}\) with line \(A D\).
23. Give an alternate proof of the fact the quadrilateral of any associated Saccheri quadrilateral of a triangle is, in fact, Saccheri as follows. Start as before but take \(\mathrm{F}_{1}\) along ray \(\mathrm{DM}\) with \(\mathrm{MF}_{1} \cong \mathrm{MD}^{\mathrm{M}}\) and \(\mathrm{F}_{2}\) along ray EN with \(\mathrm{NF}_{2} \cong \mathrm{NE}\). Prove that \(\mathrm{F}_{1}=\mathrm{F}_{2}=\mathrm{F}\), the unique perpendicular from A line \(\mathrm{MN}\) and conclude, as before, that the resulting quadrilateral BDEC is Saccheri with summit BC.
24. Prove that if the opposite sides of a quadrilateral are congruent, the figure is a parallelogram.
25. Prove that the opposite sides of a quadrilateral are congruent if and only if its diagonals bisect each other.
26. Prove that the perpendicular bisector of one side of triangle is perpendicular to the line which joins the midpoints of the other two sides. [Hint: Think of an associated Saccheri quadrilateral.]
27. Missing in the list of triangle congruency theorems SAS, SSS, ASA, and AAS is ASS. Beyond the lack of decorum, there is very good reason; the information is insufficient to guarantee congruence unless the angle is known to be a right angle in which case it is true but called "Hypotenuse-Leg". Show by explicit example that there exists two non-congruent triangles with the hypotheses of ASS satisfied.
28. Clearly the Exterior Angle Theorem does not hold on a sphere (e.g., two longitudinal lines through the North Pole and the Equator). Explain where the standard proof of the exterior angle goes wrong (as it must). Include a good sketch(es) to support your answer. If you can, characterize (i.e., find necessary and sufficient conditions for) when it is valid. [Hint: To fail, the triangle has to be big in some sense. What is that sense and how big is too big?]
29. Prove that the following construction for the tangents to a circle from a point outside of a circle to the circle is valid: Let the circle be centered at \(\mathrm{O}\) and let \(\mathrm{P}\) be the point outside of the circle. Construct a (if any) tangent from P to the circle.

Construction: Assuming the center O has been constructed, let A be the intersection of segment OP with the circle and construct the perpendicular to line OP at A. Construct circle \((O ; O P)\), the circle centered at \(O\) of radius OP and let \(\mathrm{B}\) be an intersection of this line and this circle. Finally, let \(\mathrm{T}\) be the intersection of \(\mathrm{BO}\) with the original circle. Claim: Line PT is tangent to the original circle.

[Note: This construction is a neutral geometry construction but largely unknown to US geometry students in deference to a strictly Euclidean construction (see Chapt 4). It is a little amazing in that this construction comes earlier in Euclid’s Elements, it is easier, and its proof is easier!]

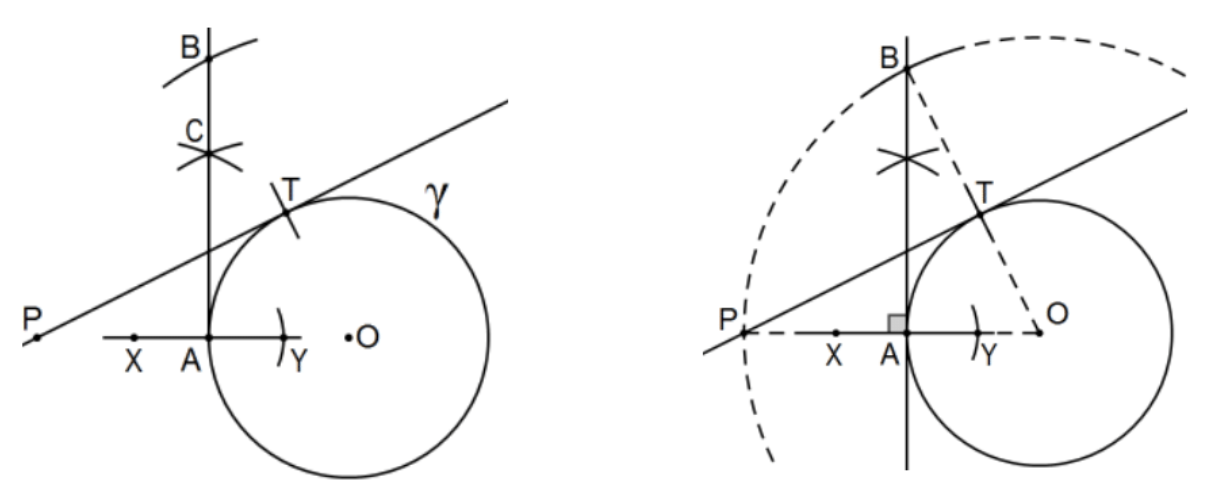
30. Prove that the line \(\mathrm{PT}\) is the only tangent on \(\mathrm{P}\) to the circle on the same side of line of the OP as point B. [Hint: Let \(S\) be a point on the circle on the same side of line \(\mathrm{OP}\) as \(\mathrm{T}\) such that line \(\mathrm{PS}\) is tangent to the circle and prove that \(\mathrm{T}=\mathrm{S}\), hence exactly one tangent on each side of line OP.]