4.1: Euclidean Geometry
- Page ID
- 107102
All of the rest of the axioms and definitions (that remain unspecified!) of neutral geometry remain in effect but in addition we add:
There exists a line and a point not on that line such that there is at most one line on that point that is parallel to the original line.
[Note: Recall from neutral geometry that we always have at least one parallel so now exactly one parallel.]
For any line and any point not on that line, there is at most one line on that point that is parallel to the original line.
These two axioms are equivalent.
Proof: Obviously, Global implies Local. Conversely, assume Local is true. Then, since the "no parallels" case does not exist (we’re in neutral geometry), the negation of Global would imply some line and some point not on that line at which there were multiple parallels. But then the global form of the Hyperbolic Parallel Postulate would imply that the given local hyperbolic situation must be true, the needed contradiction. QED.
The sum of the angles of a triangle is equal to two right angles. [So for an \(n\)-gon, exactly \(180(n-2)\).]
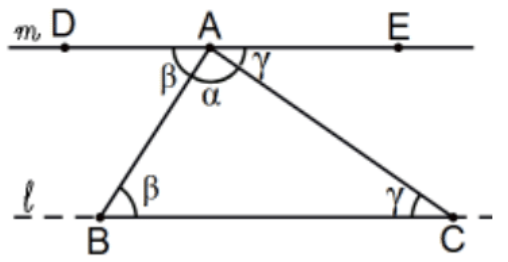
Proof: Consider any triangle, say \(\triangle \mathrm{ABC}\). At A on AB, and on the opposite side, copy \(\angle A B C\), say \(\angle D A B\), and at A on AC, and on the opposite side, copy \(\angle A C B\) to obtain \(\angle \mathrm{EAC}\). Why is line \(\mathrm{DA}=\mathrm{AE}\) so that \(\alpha+\beta+\gamma=180^{\circ}\)?
If two parallel lines are cut by a transversal, they form congruent alternate interior angles with the transversal [and alternate exterior angles and corresponding angles].
Proof: PS 4, #2. Note: This gives another easy proof of the Angle Sum Theorem - start with the parallel.
The area of square of length 1 unit is 1 square unit and, by extension, the area of any \(m \times n\) rectangle is mn square units. The area of a finite, bounded, simple (no overlaps), region (in the plane) is the greatest lower bound of the sums of the areas of all rectangles that can be inscribed inside the region with no overlap of their interiors provided that number is equal to the least upper bound of the sums of the areas of all rectangles that contain the region with no overlap of their interiors.
[Note: To prove this definition is meaningful requires more real analysis than we are going to assume.]
Two triangles are equivalent if and only if they have the same area. More generally, a triangle is equivalent to an \(n\)-gon iff they have the same area.
Proof: It should not be surprising that area would be preserved under equivalence but why not in hyperbolic geometry? That said, one proof (for triangles only) is to modify the corresponding theorem in hyperbolic geometry by replacing every occurrence of "angle sum" by “area" (PS 4, #28). Do less sophisticated proofs exist? Absolutely. For other polygons, induct on the number of sides (PS 4, #33). (This is not true for angle sum in hyperbolic geometry.) QED.
Area formulas of ordinary polygons.
If \(\triangle \mathrm{ABC}\) with sides \(\mathrm{a}, \mathrm{b}, \mathrm{c}\) is a right triangle with right angle at \(\mathrm{C}\), then \(\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}\). That is, the sum of the areas of the squares on its two legs is equal to the area of the square on its hypotenuse.
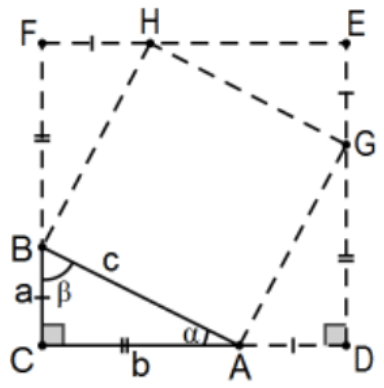
Proof 1: There are many proofs of this result; some quite different from others. Among the easiest is to build a square of sides \(a+b\) around the triangle and use a little algebra. Adding the areas of the pieces we have \((\mathrm{a}+\mathrm{b})^{2}=4((1 / 2) \mathrm{ab})+\mathrm{c}^{2}\) that simplifies to: \(\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}\). The details are left as \(\mathrm{PS} 4\), #19. QED.
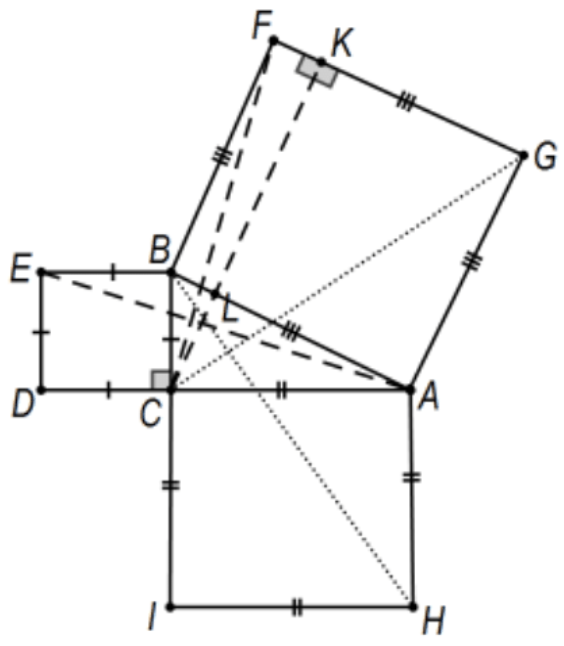
Proof 2: This is the traditional proof from Euclid’s Elements in Book 1, Prop 47 and every prospective high school geometry teacher should be familiar with it. With a little more work, it can be adjusted to prove the squares are equivalent; i.e., the two smaller squares can be "cut up" into a finite number of pieces and rearranged into the larger. In the right triangle of the figure, \(\triangle \mathrm{ABC}\), with squares on each side, assume auxiliary lines are as they appear with CK determined by the line on \(C\) perpendicular to the hypotenuse \(A B\) of the original right triangle. The area of \(\triangle \mathrm{EBA}\) is half the area of the small square BCDE (base BE and height \(\mathrm{BC}\) ) and, by SAS, \(\triangle \mathrm{EBA} \cong \triangle \mathrm{CBF}\) (rotate by \(90^{\circ}\) about point \(\mathrm{B}\) ). For the second triangle, use base BF with height BL. Thus square BCDE has the same area as rectangle BFKL. By symmetry, (segments BH and \(\mathrm{CG}\) ) square \(\mathrm{ACIH}\) and rectangle \(\mathrm{AGKL}\) have the same area. QED.
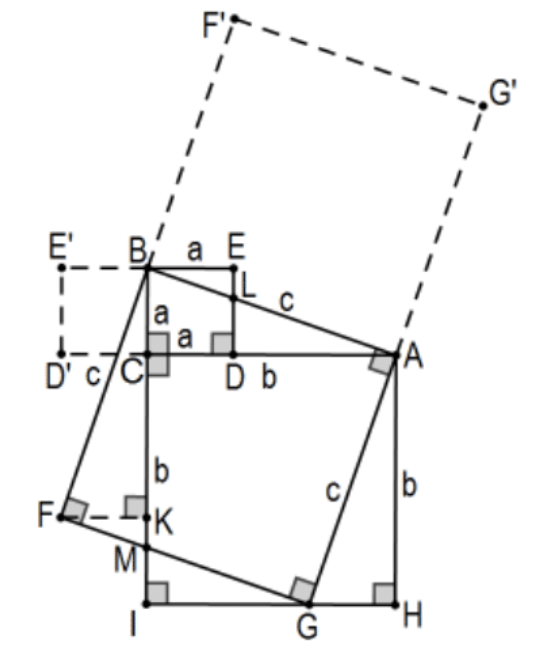
Proof 3: Much easier is a proof that directly proves that the two smaller squares are equivalent to the larger one. In this one, fold the square on one leg to overlap the triangle and fold the square on the hypotenuse across both the triangle and the adjacent squares. Note that \(\mathrm{D}^{\prime}, \mathrm{E}^{\prime}, \mathrm{F}^{\prime}\), and \(\mathrm{G}^{\prime}\) are not part of the proof; they are only there to help visualize the situation in its traditional form. Amazingly, this requires only one auxiliary line, \(\mathrm{FK}\), where \(\mathrm{K}\) is the perpendicular on \(\mathrm{F}\) to line \(\mathrm{BC}\). The idea is to show that the square on \(\mathrm{BC}\left(\mathrm{a}^{2}\right)\) together with the square on \(\mathrm{AC}\left(\mathrm{b}^{2}\right)\) is equivalent to the square on \(\mathrm{AB}\left(\mathrm{c}^{2}\right)\). Since there is so much overlap, the equivalence only requires confirming that \(\triangle \mathrm{AGH} \cong \triangle \mathrm{BFK}\), \(\triangle \mathrm{BLE} \cong \triangle \mathrm{FMK}\), and \(\triangle \mathrm{ALD} \cong \triangle \mathrm{GMI}\) and that \(\mathrm{G}\) is collinear with \(\mathrm{H}\) and I. The details are left as as PS 4 , #20. QED.
Other proofs are given in in PS 4, #21-24.
If \(\triangle \mathrm{ABC}\) is such that \(\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}\), then it is a right triangle with right angle at \(\mathrm{C}\).
Proof: Construct a right triangle with legs of size a and b. By the Pythagorean Theorem, the third side is ...? Then by SSS...? QED.
The segment joining the midpoints of two sides of a triangle is half the length of the third side and parallel to it.
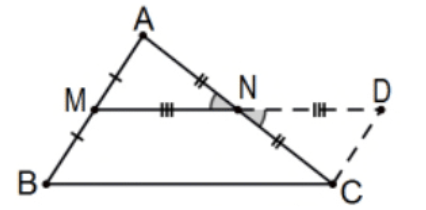
Proof: Let \(\mathrm{M}\) and \(\mathrm{N}\) be the midpoints of segments \(\mathrm{AB}\) and \(\mathrm{AC}\) of \(\triangle \mathrm{ABC}\) and double segment \(\mathrm{MN}\) to determine \(\mathrm{D}\) as indicated. With the vertical angles at \(\mathrm{N}\) we have \(\triangle \mathrm{CND} \cong \triangle \mathrm{ANM}\) by SAS. Then \(\mathrm{AM} \cong \mathrm{CD}\) and \(\angle \mathrm{DCN} \cong \angle \mathrm{A}\) by cpctc and we have congruent alternate interior angles so lines \(\mathrm{AM}=\mathrm{BM}\) and \(\mathrm{CD}\) are parallel. With \(\mathrm{AM} \cong \mathrm{BM}\) so that \(\mathrm{BM} \cong \mathrm{CD}\), we have quadrilateral BCDM with a pair of opposite sides that are both parallel and congruent. Since we are in Euclidean geometry, the quadrilateral is a parallelogram (PS 4, #15) so its opposite sides are congruent (PS 4, #12). That is, MD \(\cong B C\) and, since \(\mathrm{MN} \cong \mathrm{ND}\) by construction, \(\mathrm{N}\) is the midpoint of segment MD known to be congruent to BC. Thus we have segment MN parallel to and half of segment BC as required. QED.
Two polygons are similar (indicated “ "), and the correspondence a similarity, if (so iff) there is a proportional correspondence between their sides that preserves its angles; i.e., a 1-1 correspondence of the sides of one to the other with a positive real number r, the common ratio, such that the length of the second is the length of the first multiplied by \(\mathrm{r}\) and the angle between two corresponding sides is unchanged.
For example, \(\triangle\) MAN \(\sim \triangle B A C\) with \(r=2\) in the last theorem since the other two pairs of angles are congruent because the lines are parallel. Even more trivially, congruent figures are similar with common ratio \(r=1\).
If two triangles are such that the ratios between two of its sides are the same and the angles between those two pairs of sides are congruent, then the triangles are similar.orem text
Proof: First off, this looks like our proportion is wrong because this speaks of the ratio of two sides of the same triangle instead of the presence of a constant of proportionality for the correspondence (image side length to original side length). This fact is due to the property of ordinary fractions:
\(a / b=x / y\) iff \(a / x=b / y\) iff their reciprocals agree; i.e., \(x / a=y / b\).
Here, think of \(x\) as the length of the image of the side of length \(a\), and \(y\) likewise for \(b\), and under the correspondence that, we hope, turns out to be a similarity correspondence. Let \(r\) be that common ratio; i.e., \(r=x / a\) or \(x=r a\) and \(y=r\) b. To be proved is that, for any \(r>0\), the other 2 angles are also congruent and the third sides are in the same ratio \(\mathrm{r}\). The proof is based on induction on \(\mathrm{r}=\mathrm{n}\) as natural numbers and simple fractions \(r=1 / n\) with the new triangle with two sides and included angle superimposed on the original \(\triangle \mathrm{ABC}\) (by SAS for congruent triangles) with the two sides of length \(\mathrm{r}(\mathrm{AB})\) and \(r(\mathrm{AB})\).
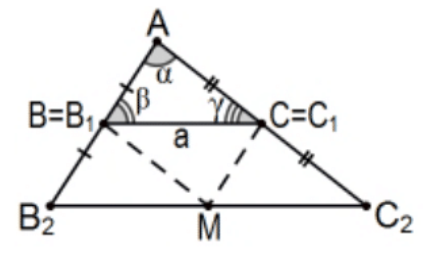
Case \(\mathrm{r}=1\): This is just SAS Congruence as mentioned above.
Case \(\mathrm{r}=2\): This is just an an immediate consequence of the last theorem. In order to prepare for a proof by Mathematical Induction, we rename the vertices as pictured, with midpoints \(\mathrm{B}=\mathrm{B}_{1}\) and \(\mathrm{C}=\mathrm{C}_{1}\) making lengths \(\mathrm{AB}_{2}=2 \mathrm{AB}\) and \(\mathrm{AC}_{2}=2 \mathrm{AC}\). By the last theorem, the length of \(\mathrm{B}_{2} \mathrm{C}_{2}=2 \mathrm{~B}_{1} \mathrm{C}_{1}\) and line \(\mathrm{B}_{2} \mathrm{C}_{2}\) parallel to line \(\mathrm{B}_{1} \mathrm{C}_{1}\) confirming \(\angle \mathrm{AB}_{1} \mathrm{C}_{1} \cong \angle \mathrm{AB}_{2} \mathrm{C}_{2}\) and \(\angle \mathrm{AC}_{1} \mathrm{~B}_{1} \cong \angle \mathrm{AC}_{2} \mathrm{~B}_{2}\). Letting \(M_{2}\) be the midpoint of segment \(B_{2} C_{2}\) determines 3 new triangles all congruent to the original \(\triangle A B C\), \(4=2^{2}\) congruent triangles.
Case \(r=1 / 2\): This time, interchange the initial triangle \(B=B_{2}\) and \(C=C_{2}\) making lengths \(A B_{1}=(1 / 2) A B\) and \(\mathrm{AC}_{1}=(1 / 2) \mathrm{AC}\), the midpoint situation of the motivating theorem above.
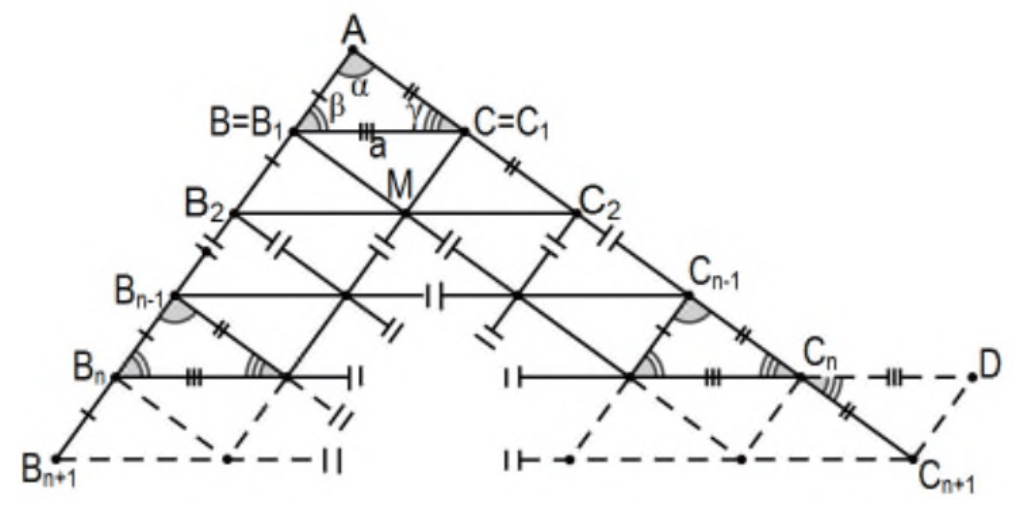
Case \(r=n\): For \(n\) any positive integer, induct on \(n\) beyond the case of \(r=2\) as follows:
Assume the result (similarity with common factor \(\mathrm{r}=\mathrm{n}\) with \(\mathrm{n}^{2}\) internal congruent triangles) is valid for \(r=2,3, \ldots, n\) and consider any triangle \(\triangle \mathrm{AB}_{\mathrm{n}+1} \mathrm{C}_{\mathrm{n}+1}\) with length \(\mathrm{AB}_{\mathrm{n}+1}=(\mathrm{n}+1) \mathrm{AB}\), length \(\mathrm{AC}_{\mathrm{n}+1}=(\mathrm{n}+1) \mathrm{AC}\), and, for convenience, the same LA. By the Ruler Postulate, identify n points to determine \(n+1\) congruent segments along each segment \(\mathrm{AB}_{\mathrm{n}+1}\) and \(\mathrm{AC}_{\mathrm{n}+1}\) by subscript number and apply the inductive hypothesis to \(\triangle \mathrm{AB}_{\mathrm{n}} \mathrm{C}_{\mathrm{n}}\). Following the proof of the the preceding theorem, extend segment \(B_{n} C_{n}\), of length \(n B C\) by the inductive hypothesis, by a segment of length \(B C\) to determine point \(D\) and consider \(\Delta C_{n+1} D C_{n}\). This triangle is congruent to the original, \(\Delta C_{n+1} C_{n} D \cong \Delta A C B\) by SAS. By cpctc of segments and angles and transitivity, \(\mathrm{DC}_{n+1} \cong \mathrm{B}_{\mathrm{n}} \mathrm{B}_{\mathrm{n}+1}\) and their lines are parallel so quadrilateral \(\mathrm{B}_{\mathrm{n}} \mathrm{B}_{n+1} C_{n+1} \mathrm{D}\) has a pair of opposite sides that are both congruent and parallel so it is a parallelogram (PS 4, #15) and its other pair of opposite sides are also congruent and parallel \((\mathrm{PS} 4, \# 12)\). Since \(\mathrm{B}_{\mathrm{n}} \mathrm{D}\) is of length \(\mathrm{nBC}+\mathrm{BC}=(\mathrm{n}+1) \mathrm{BC}\), the needed side \(\mathrm{B}_{\mathrm{n}+1} C_{\mathrm{n}+1}\) is also along with the appropriate congruence of the angles at \(\mathrm{B}_{\mathrm{n}+1}\) and \(\mathrm{C}_{\mathrm{n}+1}\) confirming similarity with \(\Delta \mathrm{ABC}\). Finally, counting the number of the internal congruent triangles, we have the original \(n^{2}\) plus \(n+1\) new ones oriented with \(\triangle \mathrm{ABC}\) and \(n\) between them oriented upside-down: \(n^{2}+(n+1)+n=n^{2}+2 n+1=(n+1)^{2}\) and the inductive step is complete. (For better understanding, carefully follow the proof with \(n=3\); the ideas are exactly the same.)
Case \(\mathrm{r}=1 / \mathrm{n}\): For any positive integer \(\mathrm{n}\) and two triangles that satisfy the SAS for Similarity conditions with common ratio \(\mathrm{r}=1 / \mathrm{n}\) (one pair of congruent angles and there including pairs of sides in the same \(1 / \mathrm{n}\) ratio), divide each of the including sides of the larger triangle, say \(\triangle \mathrm{ABC}\) into \(\mathrm{n}\) congruent segments (Ruler Postulate) and index them as with the proof of any natural number \(r=n ;\) that is \(B_{n}=B\) and \(C_{n}=C\) and each point of those subdivisions as \(\mathrm{B}_{\mathrm{i}}\) and \(\mathrm{C}_{\mathrm{i}}\) along the way. Then by \(\mathrm{SAS}\) Congruency, the smaller of the triangles is congruent to \(\Delta \mathrm{AB}_{1} \mathrm{C}_{1}\) starting from which we can recover similarity with the original \(\Delta \mathrm{ABC}\) by the case of \(r=n\).
Case \(r=m / n:\) For any positive rational number: In this case, start with either the numerator or the denominator and apply the appropriate cases in sequence.
Case \(\mathrm{r}:\) For any positive real number \(\mathrm{r}:\) If \(\mathrm{r}\) is rational, it is already done so assume \(\mathrm{r}\) is irrational. Consider any sequence of positive rational numbers that converges to \(r\) and use continuity. \(Q E D\)
If two triangles are such that the ratio between all three pairs of their corresponding sides is the same, then the triangles are similar.
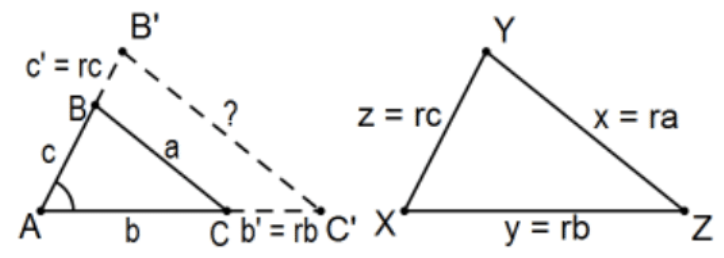
Proof: Here the constant of proportionality for the correspondence is that common ratio \(r\). It would be possible to start from scratch as in the proof of SAS Similarity but it’s not necessary. Choose two of the sides of the first triangle and consider the triangle formed by the angle between them but with the two sides r times as long. By SAS Similarity, the third side of that triangle is \(r\) times the original third side, ra. But then, by SSS Congruence,... QED.
If two triangles are such that two of its angles are congruent, then the triangles are similar.
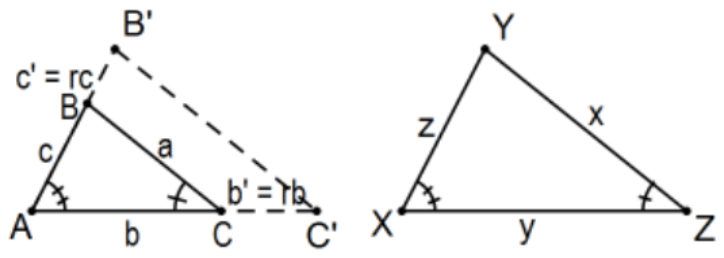
Proof: Where is the constant of proportionality for the correspondence? It is the ratio r of the sides included by the two pairs of congruent angles, \(r=y / b\).
Since there is only one pair of sides under consideration, "they" all agree and proceed as with SSS as above. More explicitly, suppose \(\triangle \mathrm{ABC}\) and \(\triangle \mathrm{XYZ}\) are such that \(\angle \mathrm{A} \cong \angle \mathrm{X}\) and \(\angle \mathrm{C} \cong \angle \mathrm{Z}\) as indicated. Multiplying the 2 sides of \(\angle A\) by the same factor \(r\), \(\mathrm{r}>0\), we have similar triangles \(\triangle \mathrm{ABC} \sim \triangle \mathrm{AB}^{\prime} \mathrm{C}^{\prime}\) by \(\mathrm{SAS}\) similarity. By definition of similarity, \(\angle \mathrm{C}^{\prime} \cong \angle \mathrm{C}\) so, by transitivity, \(\angle \mathrm{C}^{\prime} \cong \angle \mathrm{Z}\) and we have \(\triangle \mathrm{AB}{ }^{\prime} \mathrm{C}^{\prime} \cong \triangle \mathrm{X} \mathrm{YZ}\) by ASA congruence. Finally, \(\triangle \mathrm{ABC} \sim \triangle \mathrm{XYZ}\) by transitivity.
The altitude from the right angle of a right triangle divides the triangle into two triangles each similar to the original.
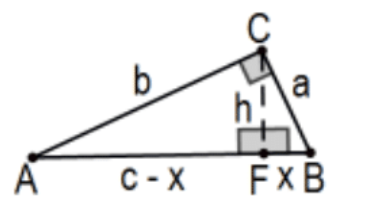
Proof: The acute angles of a right triangle are complementary so the result is immediate by AA Similarity. QED.
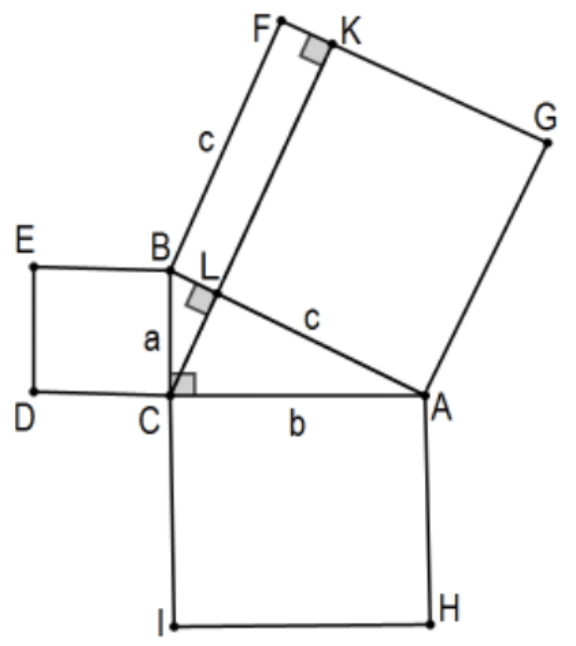
Proof 4: This fact gives the heart of yet another proof of the Pythagorean Theorem; nice in that it has the traditional picture but with a much easier proof. Starting as before with right \(\triangle \mathrm{ABC}\) with a square on each side, take the line on the right angle vertex \(C\) perpendicular to the hypotenuse so that \(\mathrm{CL}\) is the altitude from the right angle of right \(\triangle \mathrm{ABC}\). That implies that \(\mathrm{BL} / \mathrm{a}=\mathrm{a} / \mathrm{c}\) so that \(\mathrm{c}(\mathrm{BL})=\mathrm{a}^{2}\). That is, the area of square \(\mathrm{BCDE}\) is the area of rectangle BFKL. Similarly \(\mathrm{b}^{2}\) is the area of rectangle AGKL. QED. (see \(\operatorname{PS} 4, \# 21)\)
[More explicitly, the lengths of the segments of 2 transversals to 3 (or more) parallel lines are proportional (have the same ratios)].
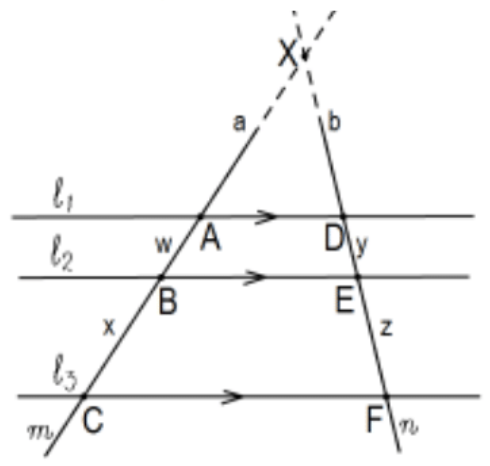
Proof: In the figure, the 3 lines \(\ell_{1}, l_{2}\), and \(l_{3}\) are parallel lines cut by transversals \(m\) and \(n\). We need to show that the determined segments are proportional; i.e., show that \(w / x=y / z\).
If the transversals \(m\) and \(n\) are parallel, the determined quadrilaterals are parallelograms so \(\mathrm{w}=\mathrm{y}\) and \(\mathrm{x}=\mathrm{z}\) and trivial equality of the ratios so assume they intersect. Let X be the intersection of \(m\) and \(n\). That determines 3 triangles, all similar by AA Similarity. The equality of the desired ratios follows from straightforward application of the similarity ratios of these triangles. The details are left as PS 4, #18.
Construct: The product and the quotient of two line segments.
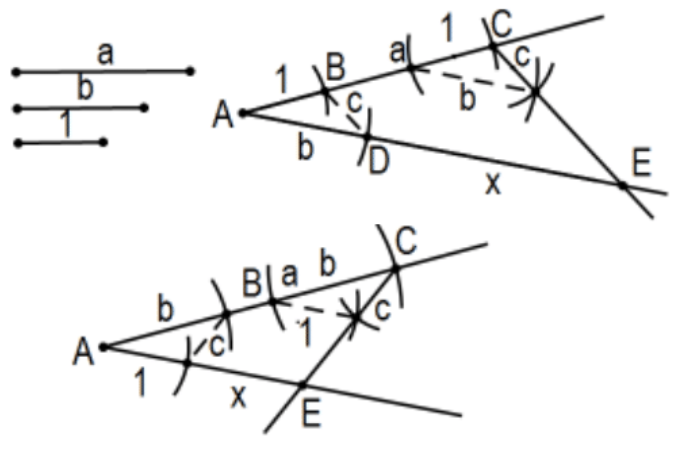
More specifically, given line segments of lengths a, \(b\), and unit length 1, construct segments of length ab and \(a / b\). and \(\mathrm{D}\) as indicated in the figure determines \(\triangle \mathrm{ABD}\). Copy \(\angle \mathrm{B}\) at point \(\mathrm{C}\) as indicated to determine point \(\mathrm{E}\) on the other ray. Then \(\mathrm{x}\), the length of segment \(\mathrm{DE}\), is the required length, \(x=a b\). For a/b, it’s the same construction except start with the b followed by a on one ray and the 1 on the other ray.
Proof: By construction, \(\angle \mathrm{ABD} \cong \angle \mathrm{ACE}\) and congruent corresponding angles implies that lines CE and BD are parallel. Since parallel lines cut off proportional segments, \(1 / b=a / x\). Therefore \(x=a b\).
Theorem: The bisector of an angle of a triangle divides the opposite side proportionately with the sides of the angle.
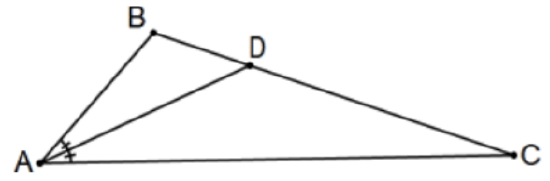
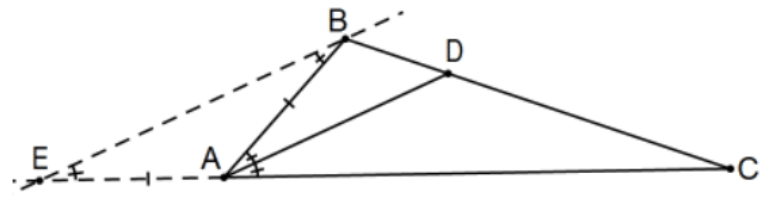
That is, in the associated figure, if ray \(\mathrm{AD}\) is the bisector of \(\angle A\), then \(\mathrm{AB} / \mathrm{AC}=\mathrm{DB} / \mathrm{DC}\).
Proof: Let \(\mathrm{E}\) be the intersection of line AC with the line on \(\mathrm{B}\) parallel to line \(\mathrm{AD}\) and consider the triangle created: \(\triangle \mathrm{DCA} \sim \triangle \mathrm{BCE}\). QED.
Corollary: The bisector of an angle of a triangle is a median if and only if the triangle is isosceles.
Theorem: Inscribed Angle Theorem: An angle inscribed in a circle has measure half the measure of its intercepted (subtended) arc; i.e., half that of its corresponding central angle.
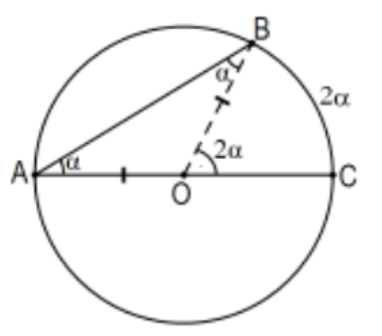
Proof: In all cases, vertex \(A\) is on the circle with center at \(O\).
Case 1: One side of the angle is a diameter. In this case, the central angle is exactly the exterior angle of the isosceles triangle determined by the inscribed angle. Explicitly, since \(\mathrm{OA}\) and \(\mathrm{OB}\) are radii of the same circle, \(\triangle \mathrm{AOB}\) is isosceles and its base angles (at \(A\) and \(B\) ) are congruent so that their sum is twice \(\alpha=m(\angle A)\). By the Euclidean form of the EAT, \(2 \alpha=2 \mathrm{~m}(\angle \mathrm{A})=\mathrm{m}(\angle \mathrm{BOC})\). Since arc measure is defined to be the measure of the central angle that subtends it, the assertion is proved.
Case 2: The center of the circle is interior to the angle. Include diameter OD: \(2 \alpha=2\left(\alpha_{1}+\alpha_{2}\right)=2 \alpha_{1}+2 \alpha_{2}\).
Case 3: The center of the circle is exterior to the angle.
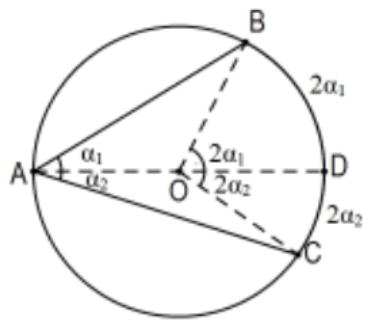
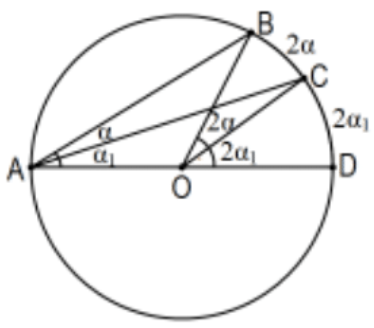
Note that \(\angle B A C=\angle B A D-\angle C A D\). This implies that \(2 \alpha=2\left(\left(\alpha+\alpha_{1}\right)-\alpha_{1}\right)=2\left(\alpha+\alpha_{1}\right)-2 \alpha_{1}\).
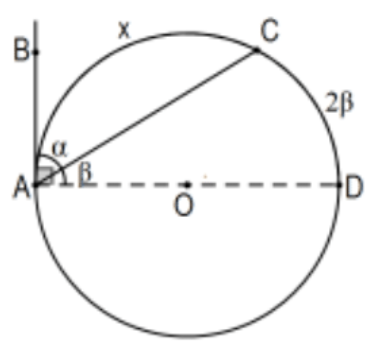
Case 4: One side of the angle is tangent to the circle. Assume line \(\mathrm{AB}\) is tangent to the circle at \(\mathrm{A}\), and that \(\angle B A C\) is acute. Consider \(\angle C A D\), the complementary angle with the diameter \(\mathrm{AD}\) determined by the radius \(\mathrm{OA}\) since, by previous theorem, lines \(\mathrm{AB}\) and \(\mathrm{AD}\) are perpendicular. Obviously, the measure of arc AC is \(\mathrm{x}=180^{\circ}-\mathrm{m}(\operatorname{arc} \mathrm{CD})\) so, by Case 1 , \(x=180^{\circ}-2 \beta=2\left(90^{\circ}-\beta\right)=2 \alpha\) and we’re done. If \(\angle B A C\) is obtuse, its supplement is acute so use the acute case and subtract from \(360^{\circ}\).
Corollary: A triangle inscribed in a semicircle (i.e., one side is a diameter) is a right triangle.
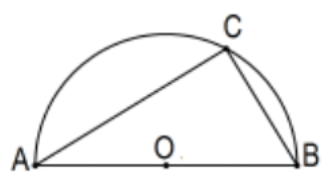
Historically, this fact is known as the Theorem of Thales. Thales was a philosopher mathematician who lived approximately 300 years prior to Euclid and has been called the first philosopher of the Greek tradition.
Corollary: Construct the tangents from a point outside a circle to the circle.
[Note: This was PS 2, #25, in neutral geometry. Why do it again? This construction is the one that is usually taught so is much better known than the earlier one. This situation is a bit strange since both constructions are in the original Euclid, Book III, the neutral geometry one is easier to prove, and is given earlier (Prop. 17 versus Prop. 31). It does make a nice example, however, of a situation where changing the axioms leaves the proposition true (the ability to construct the tangents) but the Euclidean form given here is not valid in neutral geometry. The steps of the construction can be done but, not only does the proof fail, it never produces the actual tangents!]
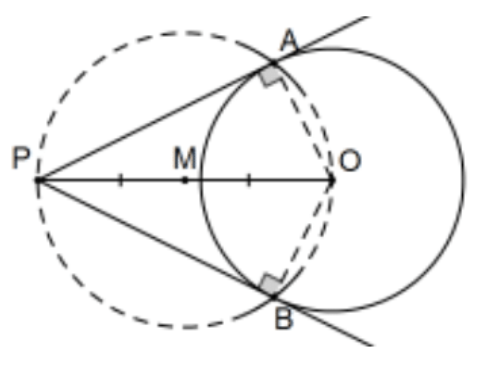
Construction: Bisect the segment determined by the point and the center of the circle and consider the circle centered at that point with radius determined by either of those points, (M; MO). Its intersections with the circle are the points of tangency. More explicitly, (if the center of the circle is not given) construct the center of the circle, \(\mathrm{O}\), the midpoint \(\mathrm{M}\) of line segment PO, and the circle with center at M and radius MP = MO. Letting \(A\) and \(B\) be the points of intersection of this circle with the original circle, the lines PA and PB are the desired tangents.
Proof: This is immediate from the theorem on triangles inscribed in semicircles. QED.
Theorem: Construct a line segment of length the square root of the length of a segment:
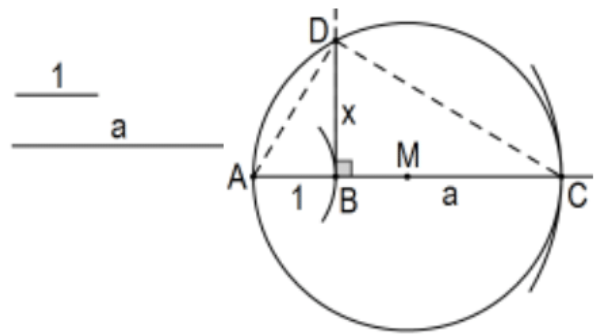
Solution: Given segments of unit length and length a, construct \(M\), the midpoint of a segment of length \(1+\mathrm{a},(\mathrm{AB}+\mathrm{BC}=\mathrm{AC}\) in the figure \()\), and the circle centered at \(M\) of radius \(M C\). Finally, construct the perpendicular at point \(B\) to determine point \(D\). Then segment BD is the required segment.
Proof: This is a triangle inscribed in a semicircle so \(\triangle \mathrm{ACD}\) is a right triangle and \(\mathrm{BD}\) is the altitude from the right angle so \(\triangle \mathrm{ADB} \sim \triangle \mathrm{DCB}\) and we have \(x / 1=a / x\) so that \(x^{2}=a\) or \(x=\sqrt{a}\). QED.
Theorem: Construct the geometric mean of the lengths of two line segments:
That is, given segments of lengths a and \(b\), solve: \(x^{2}=a b\) geometrically.
Solution: Start with \(\mathrm{m}(\mathrm{AB})=\mathrm{a}\) and \(\mathrm{m}(\mathrm{BC})=\mathrm{b}\) in the figure above. QED.
Construct all positive solutions of a quadratic equation: That is, if a, b, and c are constructible and the equation has real solutions, solve \(a x^{2}+b x+c=0\) geometrically.
Solution: For \(a x^{2}+b x+c=0, a \neq 0\), recall that the quadratic formula gives its solutions:
\(x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \quad\) Each step of the algorithm is constructible. QED.
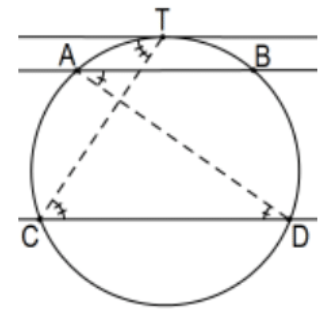
Theorem: Parallel lines intersecting a circle determine congruent arcs.
Proof: This is immediate from the Inscribed Angle Theorem.
Note: There is a problem in that we have never discussed what congruent arcs even means; everything has been in terms of breaking a figure into congruent triangles which is impossible for arcs of circles. Obviously, congruent circles are those with congruent radii. For congruent arcs, we mean arcs of congruent circles that determine congruent central angles or equivalently (by SAS congruence of triangles) congruent chords.
[Note: This is NOT true in hyperbolic geometry: ( Poincaré arc: DC \(\cong \mathrm{AB}<\mathrm{EB}\) ).]
Theorem: The Chord Theorem: For a point inside a circle, the product of the lengths of the segments determined on any chord through it is constant (i.e., \(w x=y z\) in the figure), and the measure of an angle determined by two chords through the point is half the sum of its intercepted (subtended) arcs.
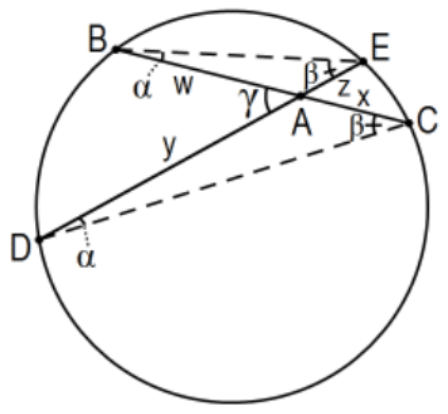
Proof: By the Inscribed Angle Theorem, \(\angle \mathrm{E} \cong \angle \mathrm{C}\) and \(\angle \mathrm{B} \cong \angle \mathrm{D}\) so, by AA Similarity, \(\triangle \mathrm{ABE} \sim \triangle \mathrm{ADC}\) so \(\mathrm{AB} / \mathrm{AD}=\mathrm{AE} / \mathrm{AC}\) or \(\mathrm{w} / \mathrm{y}=\mathrm{z} / \mathrm{x}\). Finally, \(\mathrm{wx}=\mathrm{yz}\). For the angles, \(\mathrm{m}(\angle \mathrm{BAD})=\mathrm{m}(\angle \mathrm{ABE})+\mathrm{m}(\angle \mathrm{AEB})\) by the Euclidean form of the EAT and use the Inscribed Angle Theorem to express \(\mathrm{m}(\angle \mathrm{ABE})\) and \(\mathrm{m}(\angle \mathrm{AEB})\) in terms of the arc measures of their subtended arcs. QED.
For a point outside of a circle, the product of the lengths of the external segment times its entire secant (external segment plus the chord) is constant and in the tangent case that constant is just the square of the length of the segment. The measure of the angle at the point determined by two secants is half the difference of the subtended arcs. That is and as pictured, including the tangent case, \(\mathrm{w}(\mathrm{w}+\mathrm{x})=\mathrm{y}(\mathrm{y}+\mathrm{z})=\mathrm{t}^{2}\).
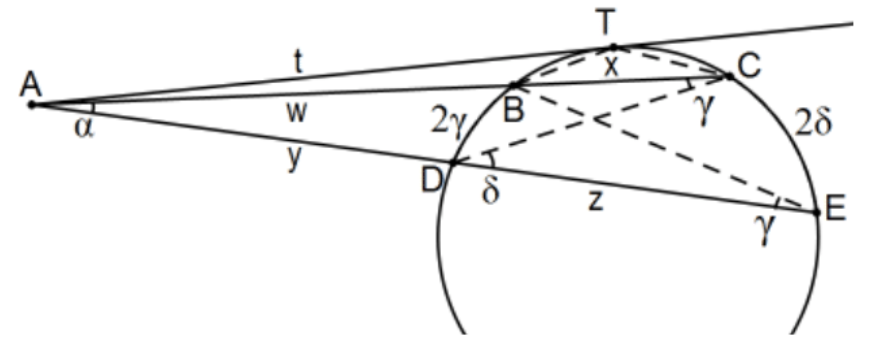
Proof: The angle at \(A\) is in common and, by the Inscribed Angle Theorem, \(\angle C \cong \angle \mathrm{E}\) so we have \(\triangle \mathrm{ABE} \sim \triangle \mathrm{ADC}\) by AA Similarity. For the constant product conclusion, \(\mathrm{AB} / \mathrm{AE}=\mathrm{AD} / \mathrm{AC}\) and cross multiply. For the angles, use the Euclidian form of the \(\mathrm{ETA}, \mathrm{m}(\angle \mathrm{CDE})=\mathrm{m}(\angle \mathrm{DAC})+\mathrm{m}(\angle \mathrm{DCA})\), or \(\delta=\alpha+\gamma\) or \(\alpha=\delta-\gamma\). Now by the Inscribed Angle Theorem with arcs \(C E\) and BD, we have \(\delta=(1 / 2)(\mathrm{m}(\mathrm{CE})-\mathrm{m}(\mathrm{BD}))\). For the tangent case, see \(\mathrm{PS} 4, \# 7\) QED.
Back in Chapter 1, we learned how to construct the center of a circle in neutral geometry; namely, choose any three points of the circle and the perpendicular bisectors of any two chords determined intersect to determine the center of the circle. This construction was familiar to many of you as a construction for the circumcircle of a triangle. That is, construct the perpendicular bisectors of two of the sides of the triangle to determine the circumcircle and the segment from that point to any of its vertices is its radius. We saw in Chapter 3 that it is not valid in neutral geometry because it is false in hyperbolic geometry; i.e., we know that some triangles have no circumcircle because sometimes those perpendicular bisectors do not intersect. In the Euclidean case, failure to intersect would imply that the two sides chosen were part the same line so that the triangle was not a triangle but a so-called "degenerate" triangle; i.e., three collinear points. Polygons with more than three sides, however, are not so clear; usually a polygon has no circumcircle but there is a surprising characterization for quadrilaterals:
A quadrilateral has a circumcircle if and only if each pair of opposite angles has sum of \(180^{\circ}\).
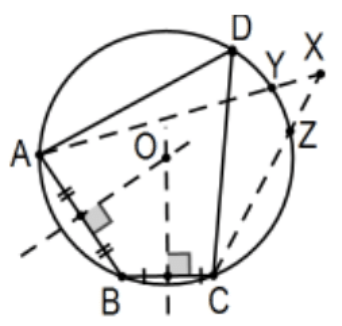
Proof: The inscribed angle theorem immediately implies that if a quadrilateral can be inscribed in a circle, opposing angles must add to \(180^{\circ}\). Conversely, suppose we have quadrilateral with opposite angles that add to \(180^{\circ}\). Use any three of the vertices to construct the circumcircle of that triangle, the triangle those three points determine and prove that the fourth vertex must lie on it as well. In essence, the chord theorem (if the point were inside) and the secant theorem (if the point were outside) would imply that the angle sum would be wrong. The details are left as Ex \(30.\)
Construct: The product and the quotient of two line segments using the chord theorem:
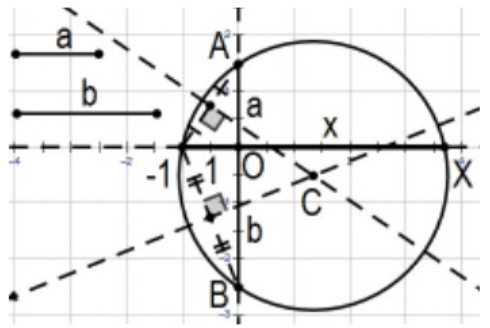
An alternate construction for the product (and for the quotient) of the lengths of two line segments of given lengths is by starting with any two intersecting lines as the lines of the their eventual chords with the constructed sum of the segments from the intersection of the lines as one of the chords and a segment of unit length from that point as one segment of the other chord. That determines 3 points of the desired circle and use them to construct the determined circle. The length of the segment from the point of intersection to the circle is the desired length (PS 4, #31). [Note: Using the \(x\) and \(y\) axes as the chord lines and the lengths as pictured, the product can be directly "read off"’ the positive \(x\)-axis \((\sim(3 / 2)(5 / 2)=15 / 4).]\)