4.4: Problem Set 4

Unless otherwise stated, assume all of the axioms of neutral geometry (albeit unstated) and the global form of the Euclidean Parallel Postulate as well.

1. Prove that the sum of the interior angles of any triangle is two right angles \(\left(180^{\circ}\right)\).
2. Prove that if two parallel lines are cut by a transversal, they form congruent alternate interior angles with the transversal.
3. Prove that a Saccheri or Lambert quadrilateral is a rectangle.
4. Construct and prove the standard Euclidean construction of the tangents from a point to a circle.
5. Prove all four cases of the Inscribed Angle Theorem. That is:

a. The center of the circle on one ray.

b. The center of the circle in the interior of the angle.

c. The center of the circle outside the angle.

d. The limit case; i.e, the case where one ray of the angle is not a chord but is tangent to the circle.

6. Prove the Chord Theorem.

7. Prove the Tangent Case of the Secant Theorem.
8. Assume in the sketch that all points and lines are as indicated along with the apparent circle with its center at \(\mathrm{O}\) and assume \(\mathrm{AB}=9, \mathrm{AF}=8, \mathrm{BC}=6, \mathrm{~GB}=4, \mathrm{GC}=7 / 2\), and \(\mathrm{GD}=6\). Find each and (briefly) explain your answer.

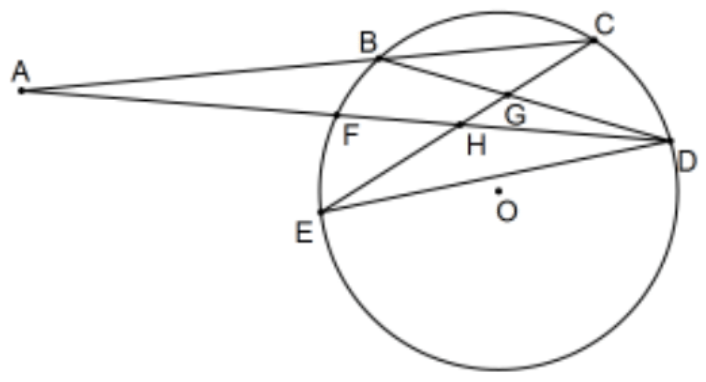
a. \(\mathrm{AC}=\)

b. \(\mathrm{AD}=\)

c. \(\mathrm{ED}=\)

d. \(F D=\)

e. \(E G=\)

9. As #8 but assume \(m(\angle A)=5^{\circ}, m(\angle E)=30^{\circ}\), and \(A B \| D E\). Find each and (briefly) explain why. [Note: NEW DATA!]

a. \(\mathrm{m}(\angle \mathrm{C})=\)

b. \(\mathrm{m}(\angle \mathrm{CBD})=\)

c. \(\mathrm{m}(\angle \mathrm{BDA})=\)

d. \(\mathrm{m}(\angle \mathrm{FDE})=\)

e. \(\mathrm{m}(\angle \mathrm{BGE})=\)

f. Prove that the data of #9 is inconsistent with the data of #8.

10. Prove that, in hyperbolic geometry, an inscribed angle is less than half its subtended arc (determined central angle) if the center of the circle is on or in the interior of the angle. The proof fails (may or may not be true) if the center is outside of the angle.

11. Conclude from Ex 10 that, in hyperbolic geometry, a triangle inscribed in a semicircle is never a right triangle. Don’t forget to confirm all 3 angles.
12. Prove that a quadrilateral is a parallelogram iff its opposite sides are congruent.
13. Prove that a quadrilateral is a parallelogram iff its opposite angles are congruent.
14. Prove that a quadrilateral is a parallelogram iff its diagonals bisect each other.
15. Prove that a quadrilateral is a parallelogram iff it has one pair of opposite sides that are both parallel and congruent.
16. Prove that if a line segment joins the midpoints of two sides of a triangle, then it is parallel to and half of its third side.

[Note: Although a much more sophisticated approach, this is immediate from a careful look at the determined associated quadrilateral.]

17. Given the unit line segment (e.g., the one in #18), construct segments of the lengths of all positive solutions to the equation: \(x^{2}-2 x-1=0\).

18. Prove that parallel lines cut off proportional segments. [More explicitly, the lengths of the segments of 2 transversals to 3 (or more) parallel lines are proportional (have the same ratios)].
19. Prove the algebraic Proof 1 of the Pythagorean Theorem as outlined in the text (there are others). If there are misconceptions as to what details must be proved, they are that the resulting figure is indeed a square of side length \(\mathrm{a}+\mathrm{b}\), that the four corners are congruent triangles and that the figure in the middle is indeed a square of side length c. "Obvious" may be tempting but it is not proof. That only works for professors and textbook authors.
20. Prove the "equivalent triangle" Proof 3 of the Pythagorean Theorem as outlined in the text.
21. Prove the "similar triangle" Proof 4 of the Pythagorean Theorem as outlined in the text.

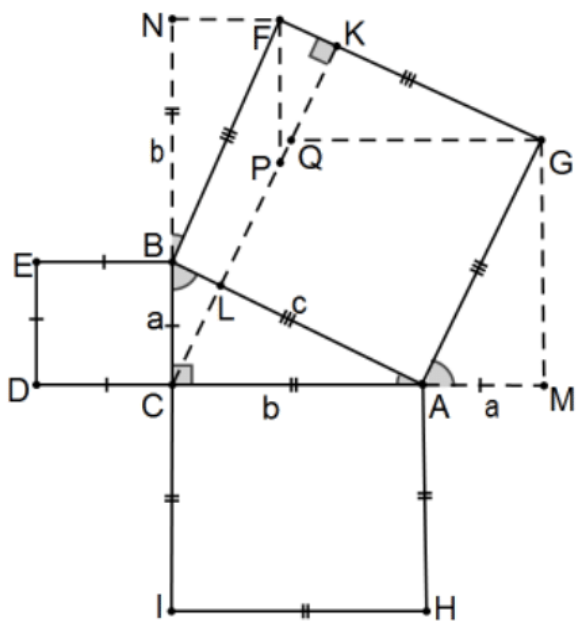
22. Prove this alternate proof of the Pythagorean Theorem indicated that avoids areas of triangles but instead uses the parallelograms BCPF and ACQG. Explicitly, extend ray CB to determine \(\mathrm{N}\) with BN of length \(b\) and \(M\) along ray CA with AM of length \(a\) and \(K\) is the foot of the perpendicular on \(\mathrm{C}\) to line \(\mathrm{FG}\). Finally, let \(\mathrm{P}\) and \(\mathrm{Q}\) be determined by the intersections with line CK and the lines parallel to BC and AC.

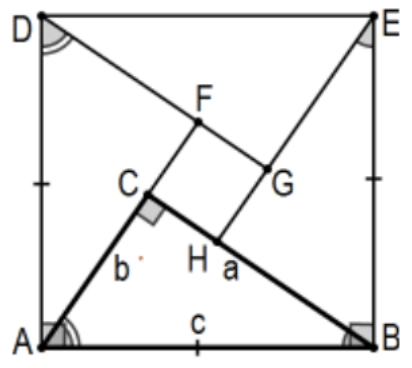
23. Prove Bhāshkara’s algebraic proof (India, b. A.D. 1114) of the Pythagorean Theorem as pictured here. ("Behold!" was his entire proof!) As usual, \(\triangle \mathrm{ABC}\) is a right triangle with right angle at \(\mathrm{C}\) with \(a \geq b\). Let segment AD be the perpendicular at A of length \(c\) and, similarly, let segment \(B E\) be the perpendicular at \(B\), also of length \(c\) to establish quadrilateral ADEB. Copy the original \(\angle \mathrm{A}\) at \(\mathrm{D}\) as indicated and the original \(\angle \mathrm{B}\) at \(\mathrm{E}\) to establish quadrilateral CFGH. Prove the Pythagorean Theorem by proving that ADEB is a square with area \(c^{2}\), CFGH is a square with area \((a-b)^{2}\), and the four triangles are all congruent with area \((1 / 2) a b\). Conclude: \(c^{2}=a^{2}+b^{2}\). [Note: What is the serious logical error in Khan’s delightful presentation? https://www.khanacademy.org/, register, and enter Bhashkar in "Search".]

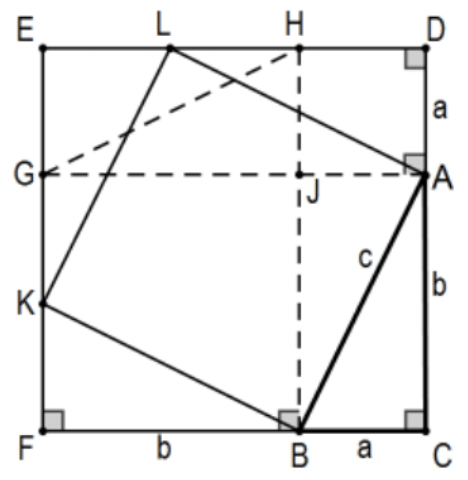
24. Here is another "Behold!" proof but I don’t know who came up with it. This time, start with the right triangle \(\triangle \mathrm{ABC}\) and extend it, equivalent to #19, to obtain the larger square as indicated by the lengths and perpendicular indicators. The resulting square consists of the 4 corners plus a square of side length c. Pairing the corner pieces and rearranging them as indicated by the dashed lines, we have the "left over" region as a square of side length a and another square of side length \(b\) ! Complete the details of a valid proof.

25. Consider the following problem: The hypotenuse of a right triangle is 10 inches and the corresponding altitude of the triangle is 6 inches. Find the area of the triangle.

i. Explain why \(\mathrm{A}=(1 / 2) \mathrm{bh}=(1 / 2)(10)(6)=30\) is wrong.

ii. Find and verify the range of possible altitudes to a hypotenuse of 10 in a right triangle.

26. Prove that the medians of a triangle are concurrent and intersect at a point \(2 / 3\) of the distance from any vertex to its opposite side. This point is called the centroid of the triangle and is its center of gravity (i.e., it would balance on that point if it were a plate of uniform thickness and density).

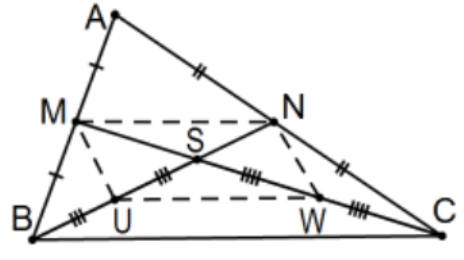
[Hint: With the given sketch, use the results of Exs. 14, 15 to prove that \(S\) is \(2 / 3\) of the way from \(C\) to \(M\) and from \(B\) to \(N\). To prove the concurrence, let \(\mathrm{T}\) be the intersection of the third median with one of these two and consider how they intersect from what has already been proved; i.e., use that to prove that \(\mathrm{T}=\mathrm{S} .]\)

Note: The intent was a so-called "synthetic" proof (as indicated) but, in Euclidean geometry, so-called "analytic" proofs are also available for more advanced theorems after similar triangles and the Pythagorean Theorem (needed for the distance formula) have been proved and assuming that the axioms of Euclidean geometry are "categorical". That is, proving the theorem in one model is tantamount to proving the theorem in all models. Although any (general) assignment of coordinates will suffice, the algebraic arithmetic (and hence, clarity) is simplified immensely by wisely choosing the assignment of coordinates to the points needed in the proof.

27. Give an analytic proof of the result of Ex. \(26 .\)

[Hint: A good way to start to let one vertex be at the origin and one side be along the \(x\)-axis so that the general triangle \(\triangle \mathrm{ABC}\) has coordinates \(A=(0,0), \mathrm{B}=(\mathrm{b}, 0)\), and \(\mathrm{C}=(\mathrm{c}, \mathrm{d}) .]\)

28. Prove the Parallelogram Law: In a parallelogram, the sum of the squares of the diagonals is equal to the sum of the squares of all four sides.

[Note: The easiest (non-vector) proof I know is analytic. Let ABCD be the parallelogram. Coordinatize with the origin at \(\mathrm{A}=(0,0), \mathrm{B}=(\mathrm{b}, 0), \mathrm{D}=(\mathrm{c}, \mathrm{d})\) and confirm that \(\mathrm{C}=(\mathrm{b}+\mathrm{c}, \mathrm{d})\). Now calculate the length of each of the segments involved .]

29. Complete the proof that two triangles of the same area are equivalent by modifying the corresponding theorem about triangles of the same angle sum in hyperbolic geometry.

[Note: This is not the traditional proof of the fact that has been known from antiquity but it is natural from our presentation.]

30. Complete the proof that a quadrilateral has a circumcircle if and only if each pair of opposite angles are supplementary (has sum of \(180^{\circ}\) ). [Hint: The figure in the text is helpful. Secant theorem? Chord theorem?]

31. Construct the product of the lengths of two line segments of given lengths by starting with any two intersecting lines as the lines of the their eventual chords with the constructed sum of the segments from the intersection of the lines as one of the chords and a segment of unit length from that point as one segment of the other chord. That determines 3 points of the desired circle and use them to construct the determined circle. The length of the segment from the point of intersection to the circle is the desired length. Use the Chord Theorem to prove the construction is valid. Finally, make the appropriate adjustments to construct the quotient of the lengths (the proof is essentially the same).

32. Greek Diameter of the Earth The ancient Greeks not only knew the earth was a sphere, they knew its size with reasonable accuracy. In \(240 \mathrm{BC}\), Eratosthenes estimated the diameter of the earth by measuring the angle formed at the top of a vertical pole that subtended its shadow at a point a known distance directly north of another point when the sun was directly overhead of the first point where a pole would have no visible shadow (he used the sun shining on the bottom of a well). There are a couple of approaches using this idea to approximate the circumference (equivalently, the diameter or radius) of the earth and both begin with the same setup described as follows.

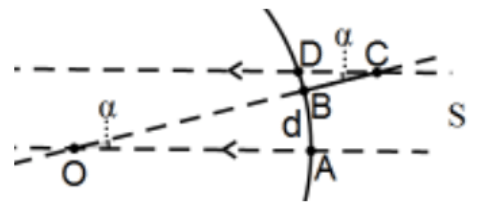
Only the northern point is needed if it is at a known distance directly north of the great circle determined by a point with sun directly overhead at a given time on a given day. Suppose the accompanying figure is the cross-section of the earth determined by the plane of \(\mathrm{O}, \mathrm{S}\) and \(\mathrm{B}\); respectively, the center of the earth, the center of the sun (too far away on the right to be visible), and a point a known distance \(\mathrm{d}\) directly north of the point A at which the sun is directly overhead (for simplicity, on the equator, at noon on an equinox). Both ideas assume that the sun is so far away that we can consider the sun’s rays to be parallel instead of radiating from the point source \(S\). Think of the line \(S O=A O\) as a light ray from the sun and the other line is the parallel ray through \(C\), the top of a vertical pole erected at \(B\). Let D be the point where that ray strikes the earth. Since line OC is a transversal to two parallel lines, \(\angle \mathrm{AOB} \cong \angle \mathrm{BCD}\) because they are alternate interior angles formed by a transversal to parallel lines and let \(\alpha=\mathrm{m}(\angle \mathrm{AOB})=\mathrm{m}(\angle \mathrm{BCD})\).

32a. Eratosthenes used the simple observation that the central angle measure \(\alpha^{\circ}\) compared with the full circle \(360^{\circ}\) is proportional to the arc length \(\mathrm{d}\) compared with the Earth’s (the circle’s) circumference c. Symbolically, we have \(\alpha / 360=\mathrm{d} / \mathrm{c}\) so that \(\mathrm{c}=360 \mathrm{~d} / \alpha\). Following Eratosthenes, approximate the circumference of the earth for \(\mathrm{d} \sim 575 \mathrm{mi}\) and \(\alpha \sim 7.2^{\circ}\) (it is hard to measure angle \(\alpha\) so accurately).

32b. Assuming point \(B\) is not too far from \(A\) (relatively small \(\alpha\) ), it is reasonable to consider the earth to be flat (it certainly feels flat!) and we replace arc AD by the common perpendicular to the two parallel lines through point B yielding points A’, D’, and, with Earth’s radius \(r\), two similar, \(\mathrm{r} / \mathrm{BA}^{\prime}=\mathrm{BC} / \mathrm{BD}^{\prime}\) from which we have the obvious approximation: \(\mathrm{r} / \mathrm{m}(\operatorname{arc}(\mathrm{BA})) \sim \mathrm{BC} / \mathrm{m}(\operatorname{arc}(\mathrm{BD})\) and finally:

\(\mathrm{r} \sim(\mathrm{m}(\operatorname{arc}(\mathrm{BA})))\left(\mathrm{BC} / \mathrm{m}\left(\operatorname{arc}\left(\mathrm{BD}^{\prime}\right)\right)\right)\) with everything on the right easily measured (easy to measure \(\mathrm{m}(\operatorname{arc}(\mathrm{BD} \mathrm{m}(\operatorname{arc}(\mathrm{BD}) \sim 11 / 2 \mathrm{ft}\) for pole length \(\mathrm{BC}=10 \mathrm{ft}\). Sketch the situation and approximate the radius of the earth \(r\) and its circumference C.

33. Use Ceva’s Theorem to prove that the medians of a triangle are concurrent. [Hint: Absolutely trivial!]

34. Use Ceva’s Theorem to prove that the angle bisectors of a triangle are concurrent. [Hint: Use the theorem that an angle bisector of a triangle divides the opposite side proportionally with the sides of the angle.]
35. In Euclidean geometry, two polygons are equal in area if and only if they are equivalent. [The formal proof is by induction on \(n\), the number sides in the polygon, as being equivalent to some triangle, so then the triangle case completes the solution. That is, for two polygons of number of sides m and \(n\) of the same area, reduce them both to triangles of the same area, use the fact that these two are equivalent and then , by symmetry and transitivity, conclude that the original polygons are equivalent. Rather than formally proving this, explain the reduction of this hexagon ABCDEF to the triangle FHJ by, one-by-one, replacing a vertex with an edge while maintaining the same area because of equivalence (i.e., "snipping off" and moving congruent triangles.)]

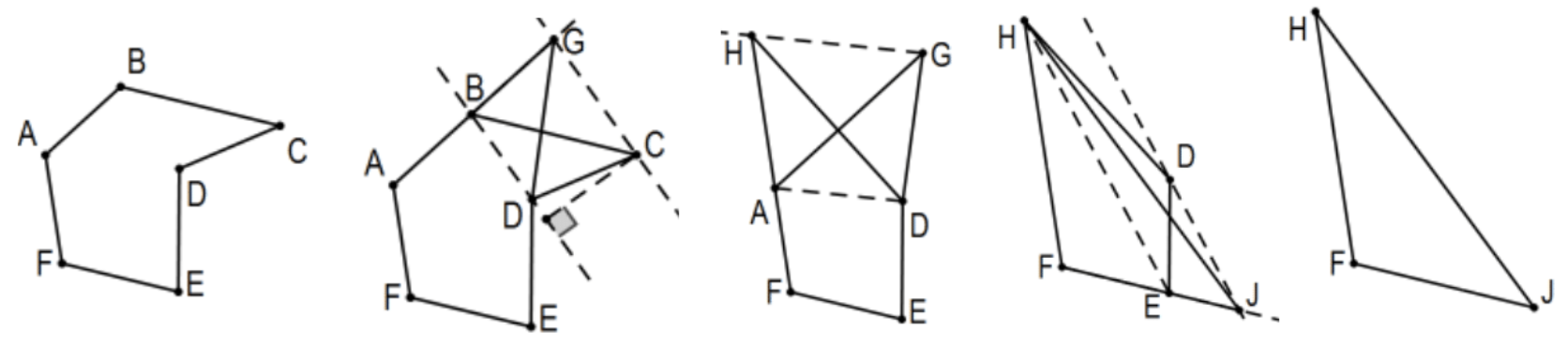
Although angle sum replaces area for triangles in the corresponding theorem in hyperbolic geometry, the natural generalization to polygons is not true. The idea looks like it might work by "cutting off" a triangle to reduce the number of vertices by using the line of midpoints and Saccheri quadrilaterals. That is, in the first step above, instead of the parallel on C to line BD (that is not unique), start with the intersection of line \(A B\) and the line of midpoints of segments \(B C\) and \(D C\) and double the segment from \(B\) to the point of intersection to establish point \(\mathrm{G}\) thereby eliminating vertex B. In the Euclidean case, that approach determines exactly the same point G. Eliminating a vertex with an equivalent polygon reduces the angle sum by exactly \(180^{\circ}\), the importance of the construction. Problem? There may not be \(180^{\circ}\) "to spare". To see why this is is so, consider the regular quadrilateral ABCD pictured in this Poincaré model, the angle sum is much less than \(180^{\circ}\) ( each angle is less than \(45^{\circ}\) ) so no vertex can be removed to obtain an equivalent triangle because it would have to have angle sum exactly \(180^{\circ}\) less but this is impossible.

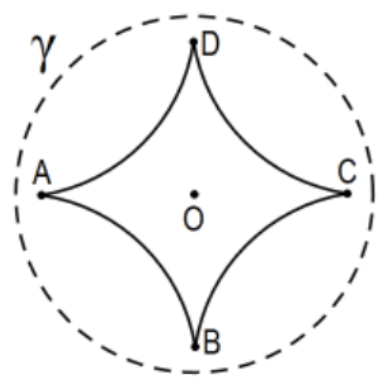
36. What goes wrong with the Euclidean proof in the hyperbolic situation?