4.3: Theorems of Ceva and Menelaus

Last updated
Save as PDF

Page ID: 104979

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Cevian (from the $17^{\text {th }}$ century Italian mathematician Giovanni Ceva (cheh’va)) is a line of a triangle from a vertex to a (non-vertex) point of the line of the side opposite. As examples, the medians of a triangle, its angle bisectors, and its altitudes are all Cevians, but they need not be anything so special. Three of them together, however, do lead to a surprising and powerful result. The theorem was proved by Ceva but it was also proved much earlier by Al-Mu’taman ibn Hüd, an eleventh-century king of Zaragoza, Spain.

Note

To this point we have used positive measures only but this theorem uses negative measures as well. It doesn’t matter which direction on a line we call positive but, once that decision is made, all other measures on that line are consistent that and reversing the endpoints of a line segment reverses its sign.

Theorem (Ceva’s Theorem)

Cevians from each vertex are concurrent if and only if the product of the signed ratios they determine on each side line is 1 . That is, in the figure, the Cevians $\mathrm{AE}, \mathrm{BF}$, and $\mathrm{CD}$ are concurrent if and only if $(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=1$.

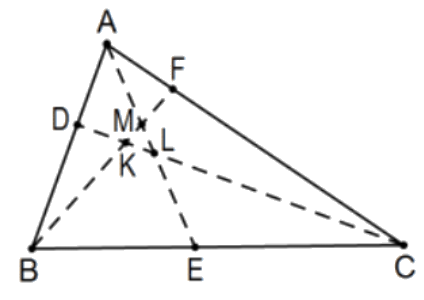
$Screen Shot 2022-06-25 at 5.57.30 PM.png$

Proof: Whether or not the Cevians are concurrent, consider the line on A parallel to line $\mathrm{BC}$ and let $\mathrm{B}^{\prime}$ be its intersection with line BF and $\mathrm{C}^{\prime}$ its intersection with CD. Even without common intersection of the Cevians, congruent alternate interior angles and vertical angles verify five pairs of similar triangles; $\mathrm{D}$ and $\mathrm{F}$ imply that $\triangle \mathrm{AC}{ }^{\prime} \mathrm{D} \sim \triangle \mathrm{BCD}$ and $\triangle \mathrm{AB}^{\prime} \mathrm{F} \sim \triangle \mathrm{CBF}$ and the three with the intersections of each pair of Cevians, AE with BF, AE with CD, and BF with CD. Arbitrarily, we take directions on each line as positive if vertex to vertex or vertex to Cevian is alphabetically increasing and $A$ toward $B^{\prime}$ along the remaining.

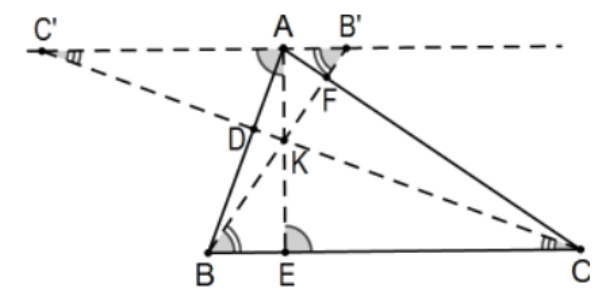
$Screen Shot 2022-06-25 at 5.58.56 PM.png$

These lead to many pairs of equal ratios including:

$\left(\mathrm{AD} / \mathrm{BD}=-\mathrm{AC}^{\prime} /-\mathrm{BC}\right) \Rightarrow(\mathrm{AD} / \mathrm{DB}=\mathrm{AC} / \mathrm{CB})$ (worrying about signed measures) and
$\mathrm{CF} / \mathrm{FA}=\mathrm{CB} / \mathrm{B}^{\prime} \mathrm{A}$ (the signs of the measures already agree). Suppose these three Cevians do intersect at a single point, say $K$. Then $\triangle \mathrm{AB}{ }^{\prime} \mathrm{K} \sim \triangle \mathrm{EBK}$ and $\Delta \mathrm{AC}^{\prime} \mathrm{K} \sim \Delta \mathrm{ECK}$ so that: $\left(\mathrm{AB}^{\prime} / \mathrm{EB}=\mathrm{AK} / \mathrm{EK}=-\mathrm{AC}^{\prime} /-\mathrm{EC}\right) \Rightarrow\left(\mathrm{EB} / \mathrm{AB}^{\prime}=\mathrm{EC} / \mathrm{AC}{ }^{\prime}\right)$ (reciprocals of first and last) and
$\left(\mathrm{EB} / \mathrm{EC}=\mathrm{AB}^{\prime} / \mathrm{AC}^{\prime}\right) \Rightarrow\left(\mathrm{BE} / \mathrm{EC}=\mathrm{B}^{\prime} \mathrm{A} / \mathrm{AC}\right.$ ’) (signs again and also "interchanging the means"). Multiplying equations $(1),(3)$, and $(2)$, respectively, we have:

\[(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=(\mathrm{AC} / \mathrm{CB})\left(\mathrm{B}^{\prime} \mathrm{A} / \mathrm{AC}^{\prime}\right)\left(\mathrm{CB} / \mathrm{B}^{\prime} \mathrm{A}\right)=1 \nonumber\]

The converse is that, if the equation holds, then $\mathrm{AE}, \mathrm{BF}, \mathrm{CD}$ are concurrent. To prove this, assume that $\mathrm{K}$ is the point of intersection of only two of the Cevians, $B F$ and $C D$, and let $E^{\prime}$ be the intersection of line AK with line $\mathrm{BC}$. Then, from the part of the theorem just proved, (AD/DB) $\left(\mathrm{BE}^{\prime} / \mathrm{E}^{\prime} \mathrm{C}\right)(\mathrm{CF} / \mathrm{FA})=1$ and, by the hypothesis, we have that (AD/DB) (BE/EC) $(\mathrm{CF} / \mathrm{FA})=1$. Simple algebra yields $\mathrm{BE}^{\prime} / \mathrm{E}^{\prime \prime} \mathrm{C}=\mathrm{BE} / \mathrm{EC}$ and, adding 1 to each side and adding the resulting mixed fractions, we have $\left(\mathrm{BE}^{\prime}+\mathrm{E}^{\prime} \mathrm{C}\right) / \mathrm{E}^{\prime} \mathrm{C}=(\mathrm{BE}+\mathrm{EC}) / \mathrm{EC}$. Noticing that $\mathrm{E}^{\prime}$ is between $\mathrm{B}$ and $\mathrm{C}$ and so is $\mathrm{E}$, the numerators both simplify to BC. That is, $\mathrm{BC} / \mathrm{E}^{\prime} \mathrm{C}=\mathrm{BC} / \mathrm{EC}$. From this it follows immediately that $\mathrm{E}^{\prime} \mathrm{C}=\mathrm{EC}$ and, from their collinearity and the Ruler Postulate, E’ = E which proves that the Cevians are concurrent. QED.

Is the "signed" detail is necessary? Is it possible to have the product of these ratios to be $-1$ ? Not only is the answer "yes", the result is an important theorem in its own right. There are some nice consequences of Ceva’s Theorem. A couple of these we have already seen but are almost trivial consequences of this theorem. Truly trivial is that the medians of a triangle are concurrent. PS 4 , #26 is a nontrivial proof but also gives more information.

Slightly more involved is another proof that the angle bisectors of a triangle are concurrent. This time, the proportionality theorem for angle bisectors provides the answer (See PS 4, #33). More complicated, but indicative of the power of the theorem:

Theorem

The altitudes of a triangle are concurrent (the point of intersection is called the orthocenter).

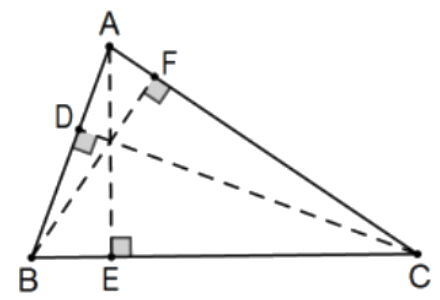
$Screen Shot 2022-06-25 at 6.00.55 PM.png$

Proof: Consider acute $\triangle \mathrm{ABC}$ and let E, F, and D be the feet of the altitudes from vertices A, B, and C, respectively. By AA Similarity: $\triangle \mathrm{CAD} \sim \triangle \mathrm{BAF}$ ( $\angle \mathrm{A}$ in common) $\triangle \mathrm{ABE} \sim \triangle \mathrm{CBD}$ ( $\angle \mathrm{B}$ in common) $\triangle \mathrm{BCF} \sim \triangle \mathrm{ACE}(\angle \mathrm{C}$ in common)

$Screen Shot 2022-06-25 at 6.03.40 PM.png$

As before, assigning positive sign from $A$ to $B, B$ to $C$, and $A$ to $C$ :

$[\mathrm{AD} / \mathrm{CA}=\mathrm{AF} / \mathrm{BA}] \Rightarrow[(\mathrm{AD} / \mathrm{CA})(\mathrm{BA} / \mathrm{AF})=1]$

$[\mathrm{BE} / \mathrm{AB}=-\mathrm{BD} /-\mathrm{CB}] \Rightarrow[(\mathrm{BE} / \mathrm{AB})(\mathrm{CB} / \mathrm{BD})=1]$

$[\mathrm{CF} / \mathrm{BC}=-\mathrm{CE} /-\mathrm{AC}] \Rightarrow[(\mathrm{CF} / \mathrm{BC})(\mathrm{AC} / \mathrm{CE})=1]$

Multiplying these three yields the equation:

\[\begin{align*} 1 &=[(\mathrm{AD} / \mathrm{CA})(\mathrm{BA} / \mathrm{AF})][(\mathrm{BE} / \mathrm{AB})(\mathrm{CB} / \mathrm{BD})][(\mathrm{CF} / \mathrm{BC})(\mathrm{AC} / \mathrm{CE})] \\[4pt]
&=[(\mathrm{AD} \cdot \mathrm{BE} \cdot \mathrm{CF})(\mathrm{BA} \cdot \mathrm{CB} \cdot \mathrm{AC}) /[(\mathrm{BD} \cdot \mathrm{CE} \cdot \mathrm{AF})(\mathrm{CA} \cdot \mathrm{AB} \cdot \mathrm{BC})] \\[4pt]
&=[(\mathrm{AD} \cdot \mathrm{BE} \cdot \mathrm{CF})(\mathrm{BA} \cdot \mathrm{CB} \cdot \mathrm{AC}) /[(\mathrm{DB} \cdot \mathrm{EC} \cdot \mathrm{FA})(\mathrm{AC} \cdot \mathrm{BA} \cdot \mathrm{CB})] \\[4pt]
&=[(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})][(\mathrm{BA} / \mathrm{BA})(\mathrm{CB} / \mathrm{CB})(\mathrm{AC} / \mathrm{AC})] \\[4pt]
&=(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA}) \end{align*}\]

By Ceva’s Theorem, lines AE, BF, and CD are concurrent.

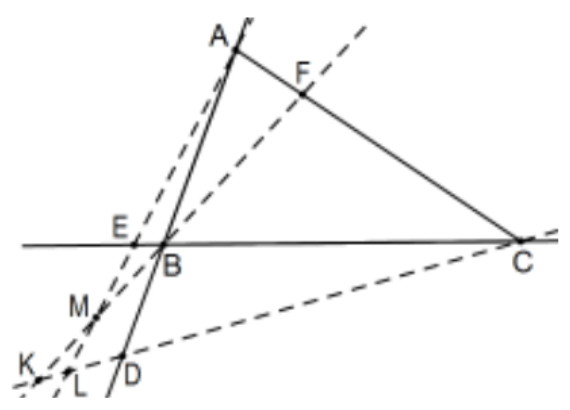
$Screen Shot 2022-06-25 at 6.08.44 PM.png$

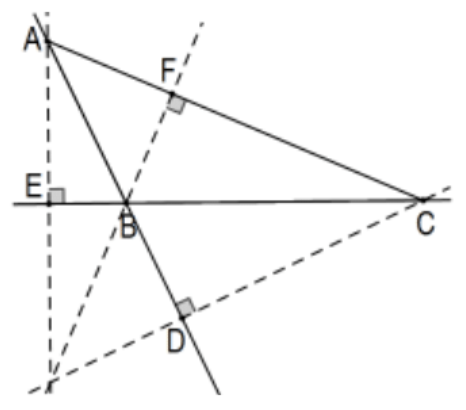
However, as the second figure implies, we do need to extend the result to obtuse triangles. Looking back at the similar triangles used in the acute case, the indicated triangles are still similar but there is a twist, the one that uses common $\angle$ B uses vertical angles instead of the common angle. Thus the ratios themselves, still hold and, checking, so do the signs of the ratios. Because of that fact, the same proof for congruence of the altitudes still works provided Ceva’s Theorem also holds for obtuse triangles. Fortunately, it does. If two of the Cevian points are outside of their corresponding sides of the triangle, Ceva’s Theorem still holds:

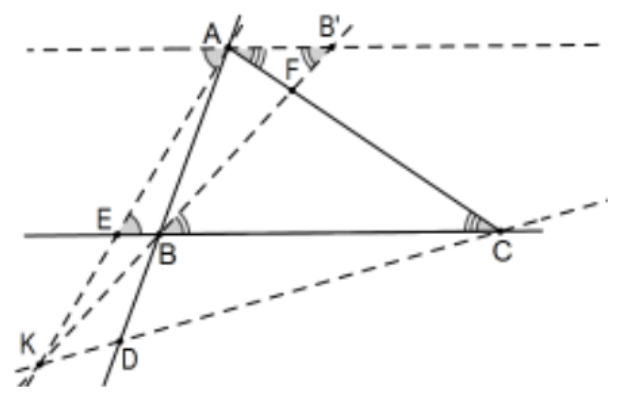
$Screen Shot 2022-06-25 at 6.09.55 PM.png$

In the figure, D is outside of segment $\mathrm{AB}$ and $\mathrm{E}$ is outside of segment BC. Assuming the direction assignments as before, this time $\mathrm{DB}$ and $\mathrm{BE}$ are negative while $\mathrm{F}$ is still between $\mathrm{A}$ and $\mathrm{C}$ so $\mathrm{CF}$ is of the same sign. Then, whether the lines intersect in a single point or not, $(AD/DB)(BE/EC)(CF/FA)$ is positive. That fact could simplify the mechanics of the proof a little in that we could ignore their signs and consider all lengths as positive, an observation that would have meant we would not have had to worry about two reversals at a time in the internal case. Proceeding exactly as before, consider the parallel on A to the opposite side line $B C$ with $B^{\prime}$ and $C^{\prime}$ ( $C^{\prime}$ is off the page to the right) as before and positive direction from $A$ toward $B^{\prime}$ so that, this time, $A C^{\prime}$ is positive. All of the identified triangles are still similar (common vertex at D and $\mathrm{K}$ instead of vertical angles) so that $\triangle \mathrm{AC}{ }^{\prime} \mathrm{D} \sim \triangle \mathrm{BCD}$ and $\triangle \mathrm{AB}{ }^{\prime} \mathrm{F} \sim \triangle \mathrm{CBF}$ and therefore:

$\left(\mathrm{AD} / \mathrm{BD}=\mathrm{AC}^{\prime} / \mathrm{BC}\right) \Rightarrow(\mathrm{AD} / \mathrm{DB}=\mathrm{AC} / \mathrm{CB})$ (worrying about signed measures ) and
$\left(\mathrm{AF} / \mathrm{CF}=\mathrm{AB}^{\prime} / \mathrm{CB}\right) \Rightarrow\left(\mathrm{CF} / \mathrm{FA}=\mathrm{CB} / \mathrm{B}^{\prime} \mathrm{A}\right.$ ) (taking reciprocals and reverse two signed measures). Suppose these three Cevians do intersect at a single point, say $K$. Then $\triangle A B^{\prime} K \sim \Delta E B K$ and $\Delta \mathrm{AC}{ }^{\prime} \mathrm{K} \sim \Delta \mathrm{ECK}$ so that $\left(\mathrm{AB}^{\prime} / \mathrm{EB}=\mathrm{AK} / \mathrm{EK}=\mathrm{AC}^{\prime} / \mathrm{EC}\right) \Rightarrow\left(\mathrm{EB} / \mathrm{AB}^{\prime}=\mathrm{EC} / \mathrm{AC}^{\prime}\right)$ and
$\left(\mathrm{EB} / \mathrm{EC}=\mathrm{AB}^{\prime} / \mathrm{AC}^{\prime}\right) \Rightarrow\left(\mathrm{BE} / \mathrm{EC}=\mathrm{B}^{\prime} \mathrm{A} / \mathrm{AC}{ }^{\prime}\right)$ ("interchanging means" and signs again). These are exactly the same three equations we had before so that, if the Cevians do intersect, then the product of the ratios is 1 . Conversely, if we assume that $K$ is the point of intersection of the two Cevians BF and $\mathrm{CD}$ and let $\mathrm{E}^{\prime}$ be the intersection of line $\mathrm{AK}$ with line $\mathrm{BC}$, we can proceed exactly as before. QED

Since Ceva’s Theorem is relatively new, it is somewhat surprising to find out that the case of $-1$ dates from antiquity with its discovery and first proof unknown. The theorem is called Menelaus’ Theorem but Menelaus was a figure from Greek mythology, not one of the great Greek geometers. As with Ceva’s Theorem, there are many proofs of this famous theorem.

Theorem (Menelaus’ Theorem)

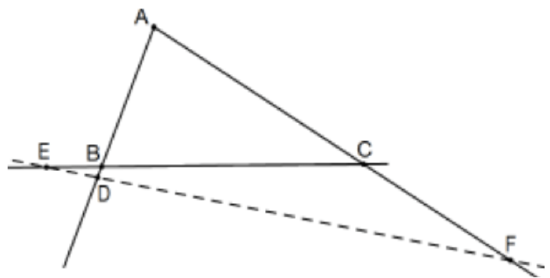
Three points, one non-vertex point from each side line of a triangle, are collinear if and only if the product of the signed ratios they determine on all three side lines is $-1$. That is, in the figure, $\mathrm{D}, \mathrm{E}$, and $\mathrm{F}$ are colinear if and only if $(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=-1$.

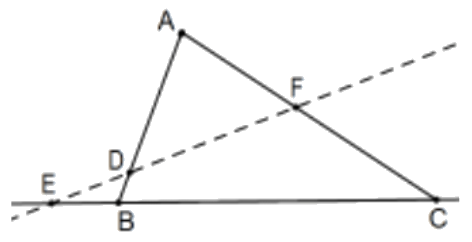
$Screen Shot 2022-06-25 at 6.16.29 PM.png$

Proof: If you haven’t already noticed, these ratios are positive if and only if the point is within the interior of its side (numerator and denominator positive or negative together). Moreover, if one of these is on the triangle itself, two must be. That is, if the three points are collinear, the line they determine intersects the interior of the sides of triangle in either two or no points and both of these are possible as the figures indicate.

That is to say, if the points are collinear, either one ratio is negative or all three are negative and, in either case, the product of ratios is negative so we do not really need to worry about signed measures; the product will be negative.

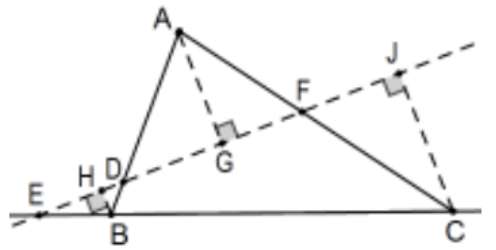
$Screen Shot 2022-06-25 at 6.19.02 PM.png$ $Screen Shot 2022-06-25 at 6.19.39 PM.png$

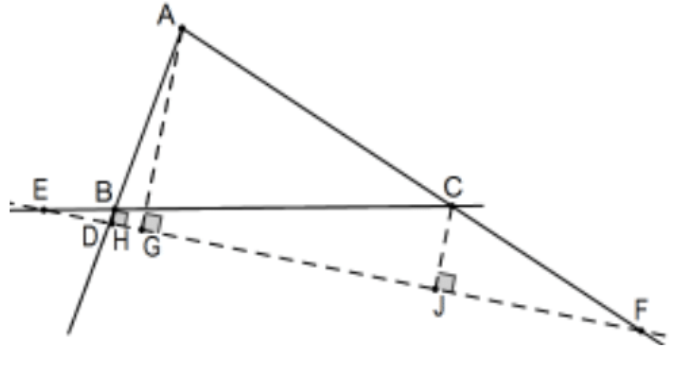
To start the proof of the case of two intersections, assume $\mathrm{D}, \mathrm{E}$, and $F$ are collinear and drop the perpendicular from each vertex. AA Similarity yields several similar triangles (E in common and vertical angles at $\mathrm{D}$ and $\mathrm{F}$ in the two-side case and, in the zero-side case, common angles at $\mathrm{E}$ and $\mathrm{F}$ and vertical angles at $\mathrm{D})$ :

$[(\mathrm{AD} / \mathrm{AG}=\mathrm{BD} / \mathrm{BH})] \Rightarrow[(\mathrm{AD} / \mathrm{BD}=\mathrm{AG} / \mathrm{BH})]$ (interchange means) $[(\mathrm{BE} / \mathrm{BH}=\mathrm{CE} / \mathrm{CJ})] \Rightarrow[(\mathrm{BE} / \mathrm{CE}=\mathrm{BH} / \mathrm{CJ})]$ (interchange means) $[(\mathrm{CF} / \mathrm{CJ}=\mathrm{AF} / \mathrm{AG})] \Rightarrow[(\mathrm{CF} / \mathrm{AF}=\mathrm{CJ} / \mathrm{AG})]$ (interchange means) From these three we have:

$(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=(\mathrm{AG} / \mathrm{HB})(\mathrm{BH} / \mathrm{JC})(\mathrm{CJ} / \mathrm{GA})$ $=(\mathrm{AG} / \mathrm{GA})(\mathrm{BH} / \mathrm{HB})(\mathrm{CJ} / \mathrm{JC})=(-1)^{3}=-1$

and Menelaus’ Theorem is proved in one direction.

$Screen Shot 2022-06-25 at 6.20.19 PM.png$

Proof of the converse follows from this result just as with Ceva. That is, assume this product is $-1$ and let $\mathrm{E}^{\prime}$ be the intersection of line DF with line BC. By the theorem just proved, we have:

\[(\mathrm{AD} / \mathrm{DB})(\mathrm{BE} / \mathrm{EC})(\mathrm{CF} / \mathrm{FA})=(\mathrm{AD} / \mathrm{DB})\left(\mathrm{BE}^{\prime} / \mathrm{E}^{\prime} \mathrm{C}\right)(\mathrm{CF} / \mathrm{FA}) \nonumber\]

and the fact that $\mathrm{E}=\mathrm{E}^{\prime}$ follows exactly as before. QED.