5.1: Advanced Euclidean Geometry

Definition: Inversion of a Point

The inversion of a point \(P \neq O\) in a circle \(\gamma\) with center \(\mathrm{O}\) and radius \(\mathrm{R}\) is the point \(\mathrm{P}^{\prime}\) on ray \(\mathrm{OP}\) such that \((\mathrm{OP})\left(\mathrm{OP}^{\prime}\right)=\mathrm{R}^{2}\).

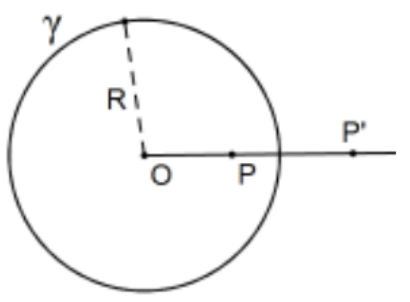
Note: Sometimes we are just thinking of the inversion of particular point P and at other times we’ll be thinking of the inversion of the entire "punctured plane". Why punctured?

Example \(\PageIndex{1}\)

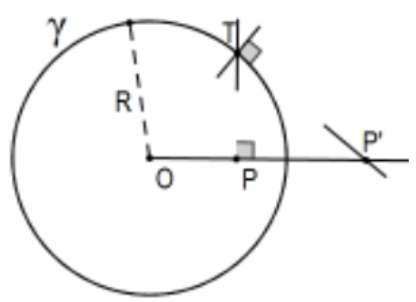
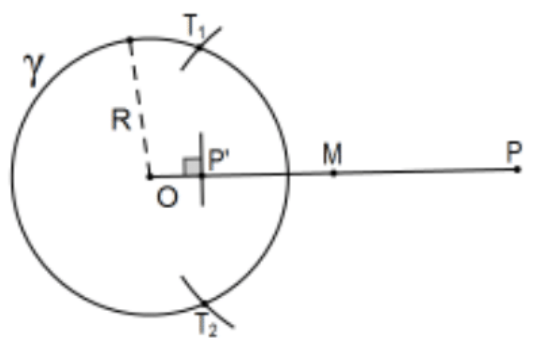
Construct the inversion of a given point \(P \neq O\) in a given circle \(\gamma\).

• Case 1: P inside the circle.
• Case 2: P on the circle.
• Case 3: P outside the circle.

Solution

For Case 1, let \(\mathrm{T}\) be (either point) determined by the perpendicular to ray \(\mathrm{OP}\) at \(\mathrm{P}\). Then \(\mathrm{P}^{\prime}\) is the intersection of ray \(\mathrm{OP}\) with the tangent at \(\mathrm{T}\), the perpendicular to the radius to \(\mathrm{T}\).

Since line \(\mathrm{TP}\) is the altitude from the right angle of right triangle \(\Delta \mathrm{OP}^{\prime} \mathrm{T}, \Delta \mathrm{TOP} \sim \Delta \mathrm{OP}^{\prime} \mathrm{T}\) so \(\mathrm{OP} / \mathrm{OT}=\mathrm{OT} / \mathrm{OP}^{\prime}\) or \(\mathrm{OP} / \mathrm{R}=\mathrm{R} / \mathrm{OP}^{\prime}\) and \((\mathrm{OP})\left(\mathrm{OP}^{\prime}\right)=\mathrm{R}^{2}\) as desired.

For Case 2, \(\mathrm{P}=\mathrm{P}^{\prime}\) so the construction instructions are "do nothing"!

For Case 3 , let \(T_{1}\) and \(T_{2}\) be the points that determine the tangent lines from \(P\). Then \(P^{\prime}\) is the intersection of ray \(O P\) with line \(T_{1} T_{2}\). (Why is this line perpendicular to line \(\mathrm{OP}^{\prime}\) ?) The proof is exactly that of Case 1 was th with the roles of \(\mathrm{P}\) and \(\mathrm{P}^{\prime}\) interchanged. QED.​​​​

Fundamental Theorem of Orthogonal Circles

If two circles \(\gamma\) and \(\delta\) intersect at points \(\mathrm{A}\) and \(\mathrm{B}\) with one of the circles centered at \(\mathrm{O}\) and \(\mathrm{P}\) and \(\mathrm{Q}\) are points of the other circle determined by a ray that originates at \(O\), then the circles are orthogonal if and only if \(P\) and \(Q\) are inversions of each other in the circle \(\gamma\) centered at \(O\).

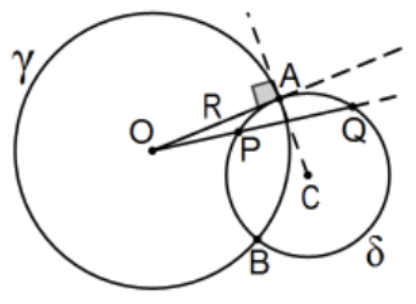
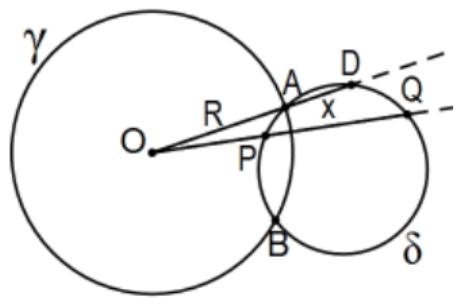
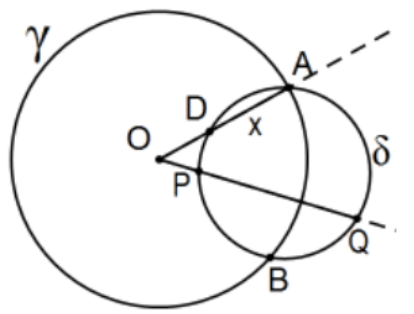
Proof: Consider ray OA. If the circles are orthogonal, then the tangent case of the secant theorem states the conclusion; i.e., \(\mathrm{OP}(\mathrm{OQ})=(\mathrm{OA})^{2}=\mathrm{R}^{2}\).

Conversely, assume \(P\) and \(Q\) are inversions in circle \(\gamma\); i.e., \(\mathrm{OP}(\mathrm{OQ})=(\mathrm{OA})^{2}=\mathrm{R}^{2}\). If the circles were not orthogonal, ray \(\mathrm{OA}\) intersects the circle at a second point, say D, and there would be a little piece of chord, \(\mathrm{AD}=\mathrm{x}\) with \(\mathrm{OA}=\mathrm{R}\) being either the internal segment of the secant of length \(R+x\) (as pictured first) or the entire secant with the external segment of length \(R-x\) (second picture). Either way, the hypothesis forces \(x\) to be 0 and \(\mathrm{OA}\) is a tangent from \(\mathrm{O}\). More explicitly, we have \(R(R \pm x)=R^{2}\). That is, \(R \pm x=R\) so that \(x=0\) and we have orthogonality.

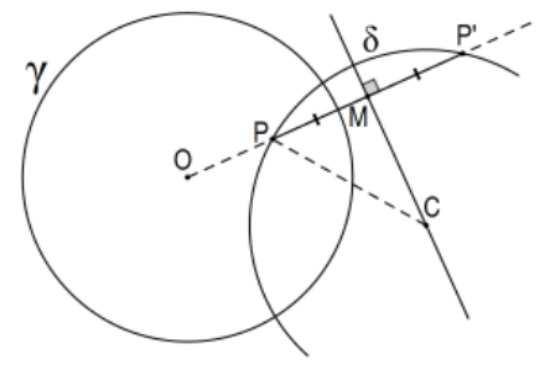
Corollary: If a point on one circle (think P on \(\delta\) ) is in the interior of another circle (think \(\gamma\) ), the circles are orthogonal if and only if the center of the first circle lies on the perpendicular bisector of the segment that joins the point with its inversion in the second circle.

Theorem: Axiom 1 for the Poincaré model.

Proof: Let \(\gamma\) be the defining circle and let A and B be distinct points of the plane not collinear with \(O\). Then \(\mathrm{A}^{\prime}\) and \(\mathrm{B}^{\prime}\) are also on the desired Euclidean circle. That makes four noncollinear points, A, B, A’, and \(\mathrm{B}^{\prime}\), any three of which completely determines the unique Euclidean circle that determines the open arc that is the desired unique Poincaré line. Moreover, the standard construction for that circle is a Euclidean construction of the Poincaré line. That is, the following is a triviality:

Corollary: Construct the Poincaré line determined by two points.

Beyond that, these additional two Euclidean points are very helpful in "eyeball" sketching the Poincaré line determined by the two points, the line on a point perpendicular to a line, the boundary parallels to a line on a point, etc. Don’t formally construct these points (although some of these are now easy formal Euclidean constructions as well; see Problem Set 5) but, if you need to, use a straightedge (edge of a book, twicefolded piece of paper, or some such) and your knowledge of orthogonal circles to sketch the Poincaré line or lines required for the problem under consideration.

[Note: This is Step 1 of a very complicated proof, that all of the axioms of hyperbolic geometry (stated herein or not) can be proved as theorems of Euclidean geometry about the Poincaré model from which we can conclude that Poincaré geometry is relatively consistent with Euclidean geometry.]

Theorem: In the inversion of the entire punctured plane in a fixed circle, circles and lines get mapped to lines and circles. More explicitly let \(\gamma\) be the fixed circle with center at \(\mathrm{O}\) and radius of length \(\mathrm{R}\). Then for any Euclidean figure \(\varphi\) that does not contain \(\mathrm{O}\), let \(\varphi^{\prime}\) indicate the inversion of all of its points in \(\gamma\) and, if \(\varphi\) does contain \(\mathrm{O}\), let \(\varphi^{*}\) be the same Euclidean figure but excluding \(\mathrm{O}\), and let \(\delta\) be any circle and \(\ell\) be any line in the Euclidean plane. Then:

i. If \(O \in \delta\), then the inversion of \(\delta^{*}\) is \(\ell\), the line perpendicular to the ray \(O C\) at \(\mathrm{D}^{\prime}\) where \(C\) is the center of \(\delta\) and \(\mathrm{D}\) is determined by the diameter of \(\delta\) determined by the ray OC.

ii. If \(\mathrm{O} \notin \ell\), then the inversion of \(\ell\) is the "punctured" circle \(\delta^{*}\) where \(\mathrm{F}\) is the foot of the /perpendicular from \(\mathrm{O}\) to \(\ell\) and \(\mathrm{OF}^{\prime}\) is the diameter of \(\delta\) (i.e., the inversion of the inversion in i).

iii. If \(\mathrm{O} \in \ell\), then the inversion of \(\ell^{*}\) is \(\ell^{*}\) (the punctured line turned inside-out).

iv. If \(\mathrm{O} \oplus \delta\), let \(\mathrm{C}\) be its center and segment \(\mathrm{AB}\) be its diameter determined by the line OC. Then the inversion of \(\delta\) is the circle \(\delta^{\prime}\) with collinear diameter \(\mathrm{A}^{\prime} \mathrm{B}^{\prime}\) with two cases to consider:

a. If \(\mathrm{O} \oplus \mathrm{AB}\), then \(\mathrm{A}^{\prime} \mathrm{B}^{\prime}\) is a subset of ray \(\mathrm{AB}\) (the case pictured), or

b. If \(O \in A B\), then \(O \in A^{\prime} B^{\prime}\) (because \(A\) and \(A^{\prime}\) are on one side of \(O\) and \(B\) and \(B^{\prime}\) are on the other).

We are especially interested in reflections of the Poincaré plane in a Poincaré line but the theorem speaks of the full Euclidean plane. Reflections in a line and rotations about any point are provable as congruences in neutral geometry, hence in hyperbolic geometry. The problem is that we do not yet know that the Poincaré disk model even is a model for hyperbolic geometry; to assume such would be assuming what we are trying to prove! (The special cases of a reflection across a diameter and a rotation about the center are obvious but not the others).

These proofs are easy but require some insight,

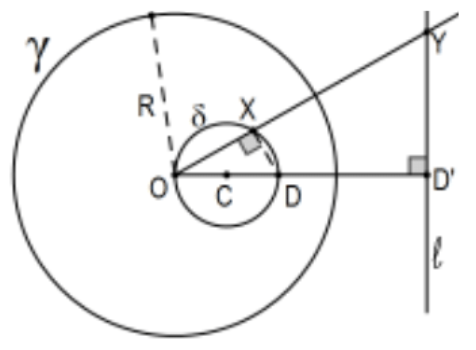
Case \(\mathrm{i}\) : Let \(\mathrm{X} \in \delta^{*}\) and let \(\mathrm{Y}=\mathrm{f}(\mathrm{X})\) be the intersection of ray \(\mathrm{OX}\) with \(\ell\), the line perpendicular to ray \(\mathrm{OC}^{\prime}\) at \(\mathrm{D}^{\prime}\). By AA Similarity, \(\triangle \mathrm{OD}^{\prime} \mathrm{Y}\) is similar to \(\triangle \mathrm{OXD}\) but so is \(\Delta \mathrm{OD}^{\prime} \mathrm{X}^{\prime}\) so that \(\mathrm{Y}=\mathrm{X}^{\prime}\) and we have \(\ell=\delta^{* \prime}\) as claimed.

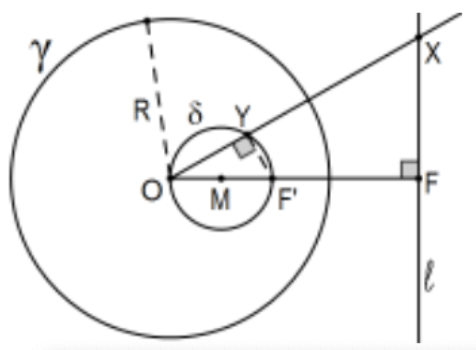
Case ii: This is exactly the same idea only this time we start with F, the foot of the perpendicular from \(\mathrm{O}\) to \(l\) and let \(\mathrm{F}^{\prime}\) be its inversion in \(\gamma\). Let \(M\) be the midpoint of segment \(\mathrm{OF}^{\prime}\). Let circle \(\delta^{*}=(\mathrm{M} ; \mathrm{MO})\); i.e., the circle with center at \(\mathrm{M}\) of radius \(\mathrm{MO}=\mathrm{MF}^{\prime}\). Let \(\mathrm{X} \in \ell\) let \(\mathrm{Y}=\mathrm{f}(\mathrm{X})\) be the point of intersection of ray \(\mathrm{OX}\) with \(\delta *\). Since \(\mathrm{OF}^{\prime}\) is a diameter, \(\triangle \mathrm{OYF}\) is a right triangle so, by AA Similarity, \(\triangle \mathrm{OYF}{ }^{\prime} \sim \triangle \mathrm{OFX}\). As before, \(\mathrm{Y}\) is the inversion of X; i.e., \(\mathrm{Y}=\mathrm{X}^{\prime}\) and we have \(l^{\prime}=\delta *\) as claimed.

Case iii: If you think about it, it’s obvious.

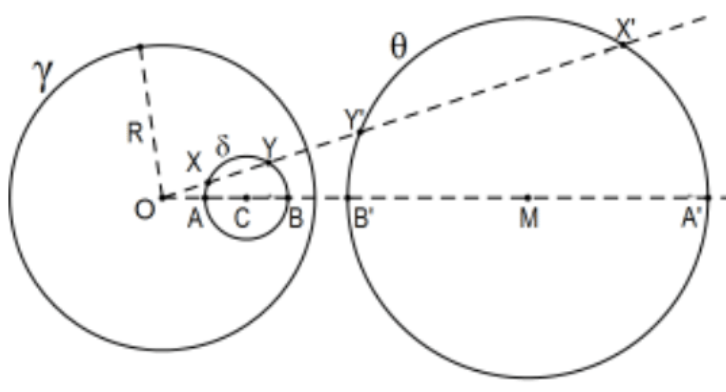
\(\underline{\text { Case iv a: }}\) The construction is easy; the figure almost says it all. For circle \(\delta\), let \(\mathrm{A}\) and \(\mathrm{B}\) be determined by line \(\mathrm{OC}\), the line of centers of the two circles and \(\mathrm{A}^{\prime}\) and \(\mathrm{B}^{\prime}\) be their inversions with \(M\) the midpoint of segment \(B^{\prime} A^{\prime}\). Then \(\delta^{\prime}=\theta\), the circle \(\left(\mathrm{M} ; \mathrm{MA}{ }^{\prime}\right)\), with center at \(M\) and radius \(\mathrm{MA}^{\prime}\). The tricky part of the proof is the idea is that the inversion of \(\delta\) is a dilation (contraction) of itself from O but only as a set, not "point-wise". That is, there exists some constant \(k\) such that every point of \(\delta^{\prime}\) is determined by a point of \(\delta\) on the ray it determines from \(\mathrm{O}\) and \(\mathrm{k}\) times its distance from \(\mathrm{O}\) (dilation for \(\mathrm{k}>1\), contraction for \(0<\mathrm{k}<1\) ). Dilations preserve circles because they preserve shapes; the ratio of any pair of distances is the same because all the factors of \(k\) cancel out. The tricky part is that the image is "turned inside out" as opposed to a "point-wise" dilation of the Euclidean plane where every point X of the plane would be mapped to the point \(\mathrm{k}(\mathrm{OX})\) from \(\mathrm{O}\) along the same ray. That is not true under inversion but, as a set of points, any circle is carried onto another circle, a dilation of itself. For any \(\mathrm{X} \in \delta\), let \(\mathrm{Y}\) be the other point determined by the ray \(\mathrm{OX}\) (if tangent, \(\mathrm{Y}=\mathrm{X}\) ). Now: \[O^{\prime}=\frac{R^{2}}{O Y}=\left(\frac{O X}{O X}\right) \frac{R^{2}}{O Y}=\frac{R^{2}}{(O X)(O Y)}(O X)=\frac{R^{2}}{(O A)(O B)}(O X) \nonumber \] Where the first equality is the definition of inversion and the last one is use of the Secant Theorem. That is, the constant we needed is \(\mathrm{k}=\mathrm{R}^{2} /(\mathrm{OA})(\mathrm{OB})\). The point is that this is a constant; i.e. it only depends on the size of the circle and its distance from \(\mathrm{O}\), not the choice of point on the circle.

[Note: Many books take the constant to be \(k=R^{2} /(O T)^{2}=(R / O T)^{2}\) where \(T\) is one of the tangents to the circle \(\delta\) from the point \(\mathrm{O}\), the same number from the tangent case of the secant theorem. The problem is that it makes Case iv b more of a special case than it needs to be.]

\(\underline{\text { Case iv b: }}\) This is the same except that the final equality holds by the Chord Theorem instead of by the Secant Theorem. This verifies the result (but with a twist; see PS 5, #10).

Lemma: For two points A and B not both collinear with the center \(\mathrm{O}\) of circle \(\boldsymbol{\gamma}\), and \(\mathrm{A}^{\prime}\) and \(\mathrm{B}^{\prime}\) the inversions of \(\mathrm{A}\) and \(\mathrm{B}\) in the circle, \(\Delta \mathrm{OA}^{\prime} \mathrm{B}^{\prime} \sim \triangle \mathrm{OBA}\); i.e., the triangles are similar but the correspondence (so the other two corresponding angles) is interchanged.

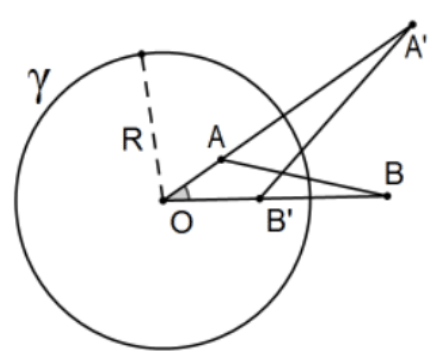
Proof: Since \(\angle O\) is in common, by SAS Similarity, we only need to check the ratio of its two sides. Letting \(R\) be the radius of the circle: \[\frac{O^{\prime}}{\mathrm{OB}}=\frac{\mathrm{R}^{2} / \mathrm{OA}}{\mathrm{OB}}=\frac{\mathrm{R}^{2}}{(\mathrm{OA})(\mathrm{OB})}=\frac{\mathrm{OB}^{\prime}}{\mathrm{OA}} \quad \text { so } \quad \mathrm{A}^{\prime} \mathrm{B}^{\prime}=\frac{\mathrm{R}^{2}}{(\mathrm{OA})(\mathrm{OB})} \nonumber \]

Theorem: Inversion in a circle preserves cross ratio. That is, if \(A, B, C\), and \(D\) are four points inverted in a circle, then \((\mathrm{A}, \mathrm{B} ; \mathrm{C}, \mathrm{D})=\left(\mathrm{A}^{\prime}, \mathrm{B}^{\prime} ; \mathrm{C}^{\prime}, \mathrm{D}^{\prime}\right)\)

Proof: This important fact is simply an application of the lemma applied to the defining ratio of cross ratio. More explicitly, assuming the circle is centered at \(\mathrm{O}\), use the lemma on every defining fraction and simplify. The numerator fraction: \[A^{\prime} C^{\prime}=\left(\frac{R^{2}}{(O A)(O C)}\right) A C \text { and } C^{\prime} B^{\prime}=\left(\frac{R^{2}}{(O C)(O B)}\right) C B \text { so that } \frac{A^{\prime} C^{\prime}}{C^{\prime} B^{\prime}}=\left(\frac{O B}{O A}\right)\left(\frac{A C}{C B}\right) \nonumber \] The denominator fraction \[\mathrm{A}^{\prime} \mathrm{D}^{\prime}=\left(\frac{\mathrm{R}^{2}}{(\mathrm{OA})(\mathrm{OD})}\right) \mathrm{AD} \text { and } \mathrm{D}^{\prime} \mathrm{B}^{\prime}=\left(\frac{\mathrm{R}^{2}}{(\mathrm{OD})(\mathrm{OB})}\right) \mathrm{DB} \text { so that } \frac{\mathrm{A}^{\prime} \mathrm{D}^{\prime}}{\mathrm{D}^{\prime} \mathrm{B}^{\prime}}=\left(\frac{\mathrm{OB}}{\mathrm{OA}}\right)\left(\frac{\mathrm{AD}}{\mathrm{DB}}\right) \nonumber \] These have the same multiplier (OB/OA) so they cancel and the cross ratio is preserved. QED.

Theorem: Inversion in a circle preserves angles formed by intersections of circles and lines.

[Note: This "circles and lines" is in the sense of the figures themselves - inversion of a circle may be a line or vice versa.]

Proof: This is a trivial consequence of elementary complex analysis, an analytic function (so any linear fractional transformation) is conformal (so angle preserving) at any point where it has a nonzero derivative. This is not quite inversion in a circle but, with proper choice of coefficients and followed by a reflection in the \(x\)-axis (conjugation), it is. This power, of course, is unavailable to us in a strictly Euclidean geometry setting so here is a synthetic geometry proof.

A number of cases must be considered, a conventional angle - the union of two rays (with a common initial point), the arc of a circle and a ray, and the union of arcs of two circles. Furthermore, the situation is different depending on whether the circle of a ray or the line of a ray of an angle contains the center of the circle of inversion - this latter situation is convenient enough to use to force it to simplify the other situations. For example, consider an angle determined by two circles that do not contain the center of the circle of inversion - we need to prove that the angle between their inversion circles is unchanged; i.e., the angle formed by their tangents at the point of intersection is the same after the inversion. Note that these are NEW tangent lines, not inversions of each other - the inversion of a line that does not contain the center of the circle of inversion, is not even a line - it’s a circle that does contain the center. For \(\angle A=\angle B A C\) for arcs \(\mathrm{AB}\) and \(\mathrm{AC}\). We need to prove that the angles between the tangents to the circles at \(\mathrm{A}\) and \(\mathrm{A}^{\prime}\) are congruent; i.e., we need to prove that conventional angles \(\angle \mathrm{SAV} \cong \angle \mathrm{UA}^{\prime} \mathrm{W}\) where \(\mathrm{S}, \mathrm{U}, \mathrm{V}\), and \(\mathrm{W}\) are any points along the rays determined by the tangent rays to the circles at \(\mathrm{A}\) and \(\mathrm{A}^{\prime}\) as indicated.

It is sufficient to "split the angle" \(\angle \mathrm{A}=\angle \mathrm{BAC}\) by line \(\mathrm{OA}=\mathrm{OA}\) ’ (that contains both angle vertices) as follows: Letting D be the other intersection of ray OA with the circle of arc AB, we can consider the original angle as two angles of the same measure sum \(\alpha=\alpha_{1}+\alpha_{2}\) where these are the measures of \(\angle\) BA and \(\angle \mathrm{DAC}\), respectively. The other special case, but handled similarly, is for \(\alpha=\alpha_{1}-\alpha_{2}\).

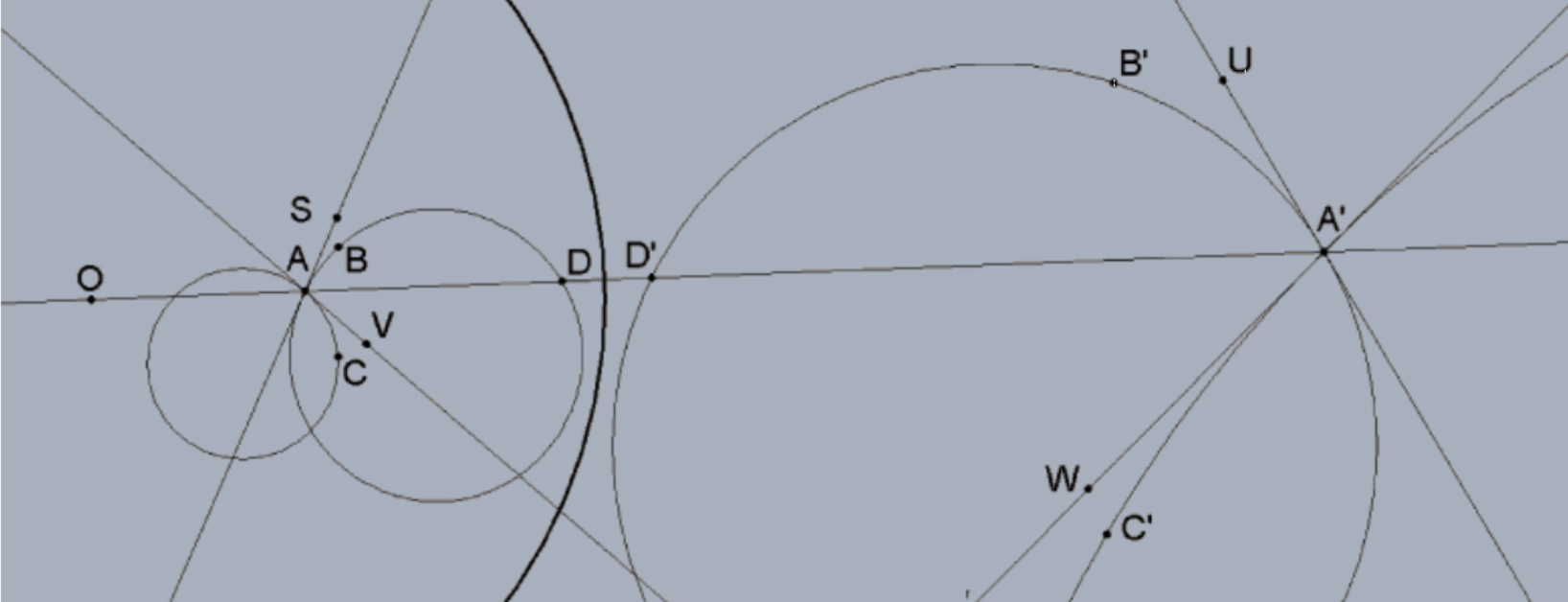
In other words, and without loss of generality, we can assume that one of the rays of the angle at A is on line OA (so we can ignore the portion of the angle below line OA). Note that in this restricted case, the inversion of the angle ray \(\mathrm{AD}\) is the other angle ray \(\mathrm{A}^{\prime} \mathrm{D}^{\prime}\) since the inversion of a (punctured) line that contains the center of the circle of inversion is the same line "turned inside out". This idea of assuming that one side of the angle is on the line determined by the center of inversion and the vertex of the angle \((\mathrm{O}\) and A, respectively) greatly reduces the number of cases needed to prove the theorem because each part of the divided angle can be considered separately and we don’t have to worry about angles with one side contained in a line through the center of inversion (all these are of that type!):

Case 1: An arc of a circle to an arc of a circle (as pictured below).

Case 2: An arc of a circle that contains the center of inversion to a ray.

Case 3: A ray within a line that does not contain the center of inversion to an arc of a circle that does.

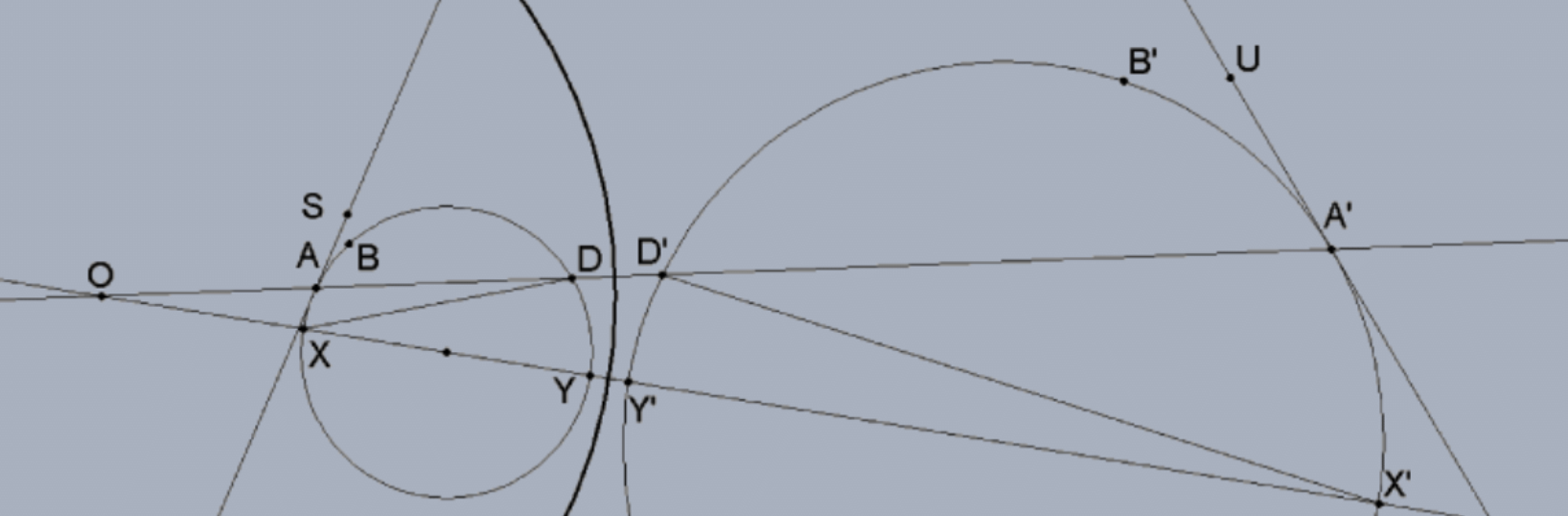
To that end, let \(X\) and \(Y\) be the diametric intersections of the circle of arc \(A B\) determined by the center of inversion \(\mathrm{O}\) and the center of the circle of arc \(\mathrm{AB}\) with inversions as indicated \(\mathrm{X}^{\prime}\) and \(\mathrm{Y}^{\prime}\). We will identify these circles by these diameters \((X Y)\) and \(\left(X^{\prime} Y^{\prime}\right)\). By previous theorem, \(\Delta O D X \approx \Delta O X^{\prime} D^{\prime}\) so that \(\angle \mathrm{ODX} \cong \angle \mathrm{OX}^{\prime} \mathrm{D}^{\prime}\). By the inscribed angle theorem (and the fact \(\angle \mathrm{ODX}=\angle \mathrm{ADX}\) ) that \(\mathrm{m}(\angle \mathrm{ADX})=(1 / 2)(\mathrm{AX})\) where \(\mathrm{AX}\) is the subtended arc of circle \((\mathrm{XY})\) and \(\mathrm{m}\left(\angle \mathrm{Y}^{\prime} \mathrm{X}^{\prime} \mathrm{D}^{\prime}\right)=(1 / 2)\left(\mathrm{Y}^{\prime} \mathrm{D}^{\prime}\right)\). Likewise, \(\angle \mathrm{OXD} \cong \angle \mathrm{OD}^{\prime} \mathrm{X}^{\prime}\) so, by supplementation, \(\angle \mathrm{DXY} \cong \angle \mathrm{X}^{\prime} \mathrm{D}^{\prime} \mathrm{A}^{\prime}\) and arc \(\mathrm{DY}\) of circle (XY) has the same measure as arc \(\mathrm{A}^{\prime} \mathrm{X}^{\prime}\) of circle \(\left(\mathrm{X}^{\prime} \mathrm{Y}^{\prime}\right)\). In each circle, the three arcs make a semcircle: \(\mathrm{XA}+\mathrm{AD}+\mathrm{DY}\) of circle (XY) and \(\mathrm{X}^{\prime} \mathrm{A}^{\prime}+\mathrm{A}^{\prime} \mathrm{D}^{\prime}+\mathrm{D}^{\prime} \mathrm{Y}^{\prime}\) of circle \(\left(\mathrm{X}^{\prime} \mathrm{Y}^{\prime}\right)\) with two of the three arcs being equal in measure. Since together they make semicircles (180 if using degree measure), we conclude that arc AD of circle (XY) has the same measure as arc \(\mathrm{A}^{\prime} \mathrm{D}^{\prime}\) of circle \(\left(\mathrm{X}^{\prime} \mathrm{Y}^{\prime}\right)\). By the tangent case of the inscribed angle theorem, \(\alpha_{1}=m(\angle S A D)=(1 / 2)(A D)=(1 / 2)\left(A^{\prime} D^{\prime}\right)=m\left(\angle U^{\prime} D^{\prime}\right)\).

Case 2: An arc of a circle that contains the center of inversion to a ray.

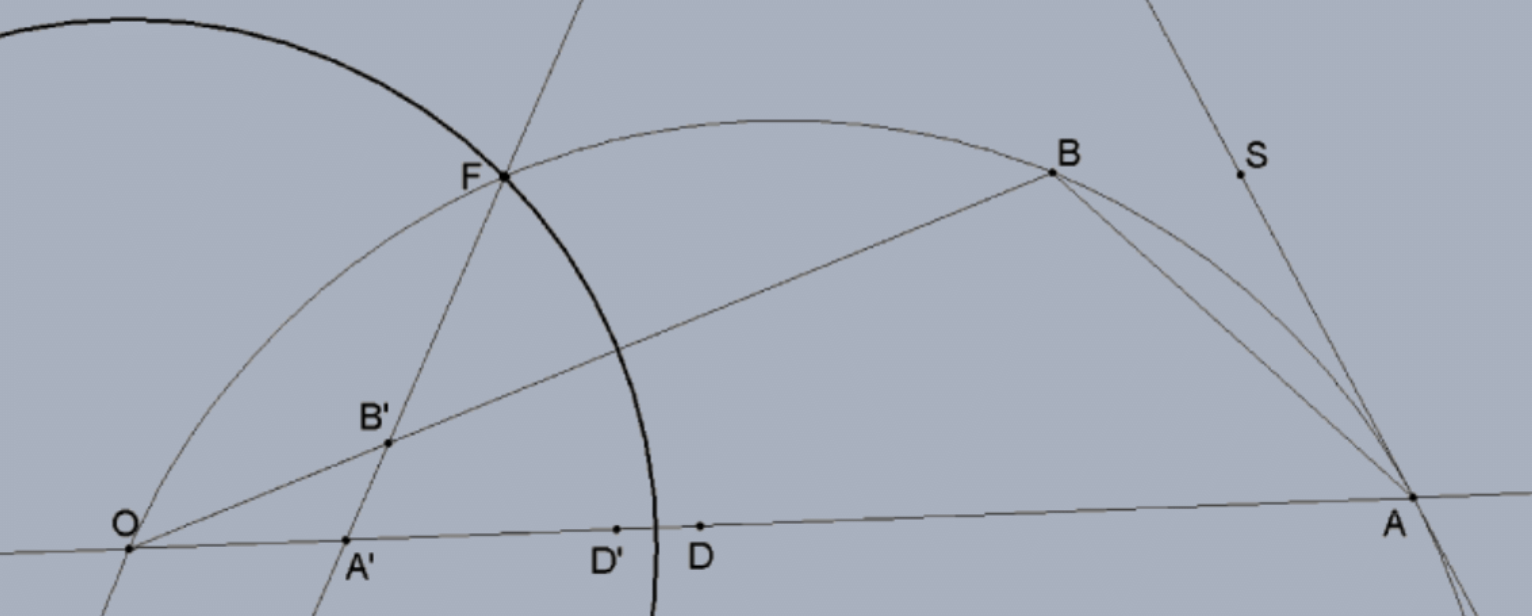
In this case, the inversion of \(\angle B A D\) where \(A B\) is an arc of a circle that contains \(O\) is the genuine angle \(\angle \mathrm{B}^{\prime} \mathrm{A}^{\prime} \mathrm{D}^{\prime}\). By previous theorem, \(\triangle \mathrm{OBA} \approx \triangle \mathrm{OA}^{\prime} \mathrm{B}^{\prime}\) so that \(\angle \mathrm{OAB} \cong \angle \mathrm{OB}^{\prime} \mathrm{A}^{\prime}\). By the inscribed angle theorem, \(\mathrm{m}(\angle \mathrm{OAB})=(1 / 2)(\mathrm{OB})\) where \(\mathrm{OB}\) is the subtended arc of the the original circle. Moreover, the rest of arc \(\mathrm{OA}\), arc \(\mathrm{BA}\), is subtended by \(\angle \mathrm{O}\) and the entire arc gives the measure of the tangent angle \(\mathrm{m}(\angle \mathrm{SAD})=(1 / 2)(\mathrm{OA})\). Now consider triangle \(\Delta \mathrm{OA}^{\prime} \mathrm{B}^{\prime}\) and its external angle at \(\mathrm{A}^{\prime}\). By the Euclidean form of the Exterior Angle Theorem, \(\angle \mathrm{B}^{\prime} \mathrm{A}^{\prime} \mathrm{D}^{\prime}\) is the sum of the two non-adjacent interior angles, the angle at \(\mathrm{O}\) and \(\angle \mathrm{OB}^{\prime} \mathrm{A}^{\prime} \cong \angle \mathrm{A}\). That is, the inversion angle at \(\mathrm{A}^{\prime}\) agrees with the tangent angle at \(A\) as needed.

\(\underline{\text { Case 3: A ray within a line that does not contain the center of inversion to an arc of a circle that does. (This }\) is the reverse of Case 2 with very similar proof.)

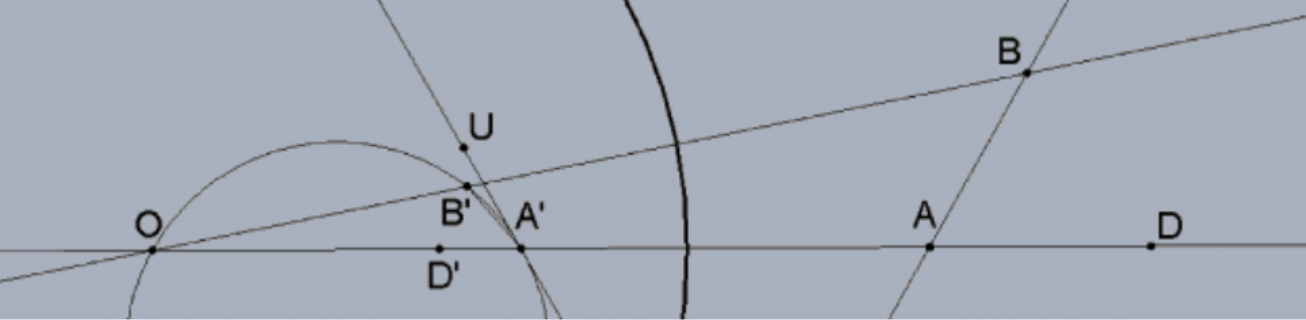
In this case, the inversion of actual angle \(\angle B A D\) is \(\angle B^{\prime} A^{\prime} D^{\prime}\) where \(A^{\prime} B^{\prime}\) an arc of a circle, the inversion of line \(\mathrm{AB}\). By previous theorem, \(\triangle \mathrm{OBA} \approx \triangle \mathrm{OA}^{\prime} \mathrm{B}^{\prime}\) so that \(\angle \mathrm{OBA} \cong \angle \mathrm{OA}^{\prime} \mathrm{B}^{\prime}\), by the inscribed angle theorem, \(\mathrm{m}\left(\angle \mathrm{OA}^{\prime} \mathrm{B}^{\prime}\right)=(1 / 2)\left(\mathrm{OB}^{\prime}\right)\) where \(\mathrm{OB}^{\prime}\) is the subtended arc of the inversion circle. Moreover, the rest of arc \(\mathrm{OA}^{\prime}\) is arc \(\mathrm{B}^{\prime} \mathrm{A}^{\prime}\) that is subtended by \(\angle \mathrm{O}\) and the entire arc gives the measure of the tangent angle \(\mathrm{m}\left(\angle \mathrm{UA}^{\prime} \mathrm{D}^{\prime}\right)=(1 / 2)\left(\mathrm{OA}^{\prime}\right)\). Now consider triangle \(\Delta \mathrm{OAB}\) and its external angle at A. By the Euclidean form of the Exterior Angle Theorem, our original \(\angle \mathrm{BAD}\) is the sum of the two non-adjacent interior angles, exactly the angle at \(\mathrm{O}\) and \(\angle \mathrm{OA}^{\prime} \mathrm{B}^{\prime} \cong \angle \mathrm{B}\). That is, the original angle at \(\mathrm{A}\) agrees with the tangent angle at \(\mathrm{A}^{\prime}\).

Does the situation change if ray AD is reversed? Slightly, and worthy of comment, but not much. The same argument together with supplementation confirms the same result. QED.

Theorem: Reflection in a Poincaré line (i.e., inversion in its Euclidean circle) is a congruence of the Poincaré plane.

Proof: We’ve done some hand-waving but the pieces are all in place. That is, angles are preserved and Poincaré distance between two points (i.e., lengths of Poincaré line segments) is preserved (at the cross ratio level). All that remains is seeing why such an inversion carries the defining disk back onto itself. It is obvious when you think about it. Explicitly, each point of the "inside" of the defining circle is inverted to its corresponding point on the "outside" and vice versa including the boundary points of the defining circle to corresponding boundary points and all points between are reversed in a similar manner. QED.

Theorem: Given any point of the Poincaré disk, there is a unique Euclidean constructible Poincaré line (i.e., Euclidean circle) such that reflection in that line carries the point onto the center of the disk.

[Note: This is an especially easy case of constructing the unique Poincaré line such that (Poincaré) reflection in that line carries any given point onto any other given point. General: PS 5, #16.]

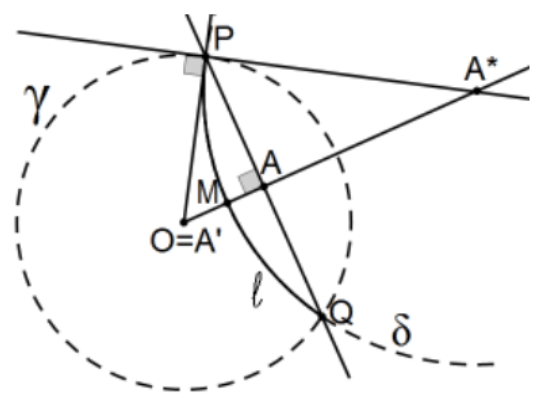
Construction: If this is to be a model for hyperbolic geometry, that there must be such a line is a consequence of neutral geometry (even though we didn’t prove it) since reflection in the perpendicular bisector of the line segment joining any two points in neutral geometry is the unique line with that property. However, we don’t yet know that this is a model so that fact is not available to us. That fact does, however, help us know how to proceed. Amazingly, if \(A\) is the point and \(\mathrm{O}\) is the center of \(\gamma\), the defining circle, the standard construction of its inversion in the circle, gives us everything! This time, however, we will identify the inversion of \(A\) in this circle by \(A *\) in order to reserve \(A^{\prime}\) for the inversion of \(A\) in the new circle yet to be located.

Letting \(P\) be the intersection of the perpendicular to the ray \(\mathrm{A}\) at \(A\) with \(\gamma\), recall that \(A *\) is determined by the perpendicular at \(P\) to the radius OP. Then the circle \((A * ; A * P)=\delta\) determines the desired Poincaré line, l. Emphasizing this conclusion, the needed circle is centered at the inversion of A in the defining circle with radius already determined in its construction!

Proof: We need to prove that \((A * A)(A * O)=(A * P)^{2}\) and that this Euclidean circle determines a Poincaré line. Orthogonality is a triviality (by construction!) and, since \(P A\) is the altitude from the right angle of \(\Delta \mathrm{OA} * \mathrm{P}, \Delta \mathrm{OA} * \mathrm{P} \sim \Delta \mathrm{PA} * \mathrm{~A}\) from which \((\mathrm{A} * \mathrm{O}) /(\mathrm{A} * \mathrm{P})=(\mathrm{A} * \mathrm{P}) /(\mathrm{A} * \mathrm{~A})\) or \((\mathrm{A} * \mathrm{~A})(\mathrm{A} * \mathrm{O})=(\mathrm{A} * \mathrm{P})^{2}\) so that \(\mathrm{O}\) is the inversion of \(A\) in this orthogonal circle centered at \(A^{*}\); i.e., it is the reflection of \(A\) in that Poincaré line. Why is there no other such circle? Inversion in a circle (reflection in a Poincaré line) preserves cross ratio so that the point of intersection, \(M\) in the figure, must be the Poincaré midpoint of segment AO. Since the center of any orthogonal circle that would carry A to \(\mathrm{O}\) must lie on ray \(\mathrm{OA}\) and the reflection would have to preserve M (i.e., not move it), this circle would have to be perpendicular to line OA as well as orthogonal to the defining circle forcing it to be the same line; i.e., uniqueness. Note that this \(l\) determines the midpoint \(\mathrm{M}\) of segment AO and is perpendicular to its line so it is the perpendicular bisector of segment AO.QED.

Lemma: One point of the Poincaré disk model is closer to the center of the defining circle than another point using Euclidean measure if and only if it is closer using Poincaré measure.

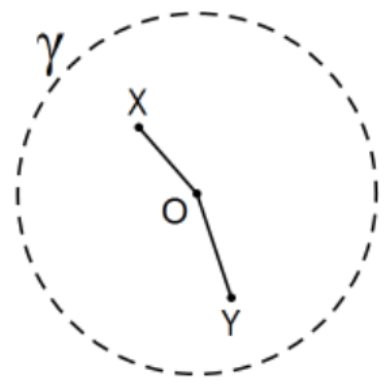
Proof: Let \(\mathrm{X}\) and \(\mathrm{Y}\) be the points with \(\mathrm{X}\) closer to \(\mathrm{O}\) than \(\mathrm{Y}\) using Euclidean measure as indicated. Rotate each segment and its diameter so that the segments are in the same direction along the same diameter. The segment lengths, whether Euclidean or Poincaré, remain unchanged but now they determine the same intersections with the defining circle and the Euclidean measures of segments \(\mathrm{OX}\) and \(\mathrm{OY}\) can be viewed as real numbers on the Euclidean number line: with \(-\mathrm{R}<0<\mathrm{x}<\mathrm{y}<\mathrm{R}\).

Comparing their cross ratios:

\((\mathrm{O}, \mathrm{X} ; \mathrm{R},-\mathrm{R})=(\mathrm{R} /(\mathrm{R}-\mathrm{x})) /(\mathrm{R} /(\mathrm{R}+\mathrm{x}))=(\mathrm{R}+\mathrm{x}) /(\mathrm{R}-\mathrm{x})\) and likewise \((\mathrm{O}, \mathrm{Y} ; \mathrm{R},-\mathrm{R})=(\mathrm{R} /(\mathrm{R}-\mathrm{y})) /(\mathrm{R} /(\mathrm{R}+\mathrm{y}))=(\mathrm{R}+\mathrm{y}) /(\mathrm{R}-\mathrm{y})\)

Although the numerators and denominators are all positive, comparison of fractions can be tricky: \(\mathrm{R}+\mathrm{x}\) is greater than \(\mathrm{R}+\mathrm{y}\) but \(\mathrm{R}-\mathrm{x}\) is also greater than R-y and a larger number divided by a larger number can be smaller.

Working in reverse from what we seek: \((\mathrm{R}+\mathrm{x}) /(\mathrm{R}-\mathrm{x})<(\mathrm{R}+\mathrm{y}) /(\mathrm{R}-\mathrm{y})\) iff \((\mathrm{R}+\mathrm{x}) /(\mathrm{R}-\mathrm{y})<(\mathrm{R}+\mathrm{y}) /(\mathrm{R}-\mathrm{x})\) iff \(R x-R y<R y-R x\) iff \(2 R x<2 R y\) iff \(x<y\). Since \(x<y\), these cross ratios satisfy the same inequality as the distances of the rotated points. However, cross ratio was not the point, only their Poincaré length; i.e., \(|\ln (\mathrm{O}, \mathrm{X} ; \mathrm{R},-\mathrm{R})|\) and \(|\ln (\mathrm{O}, \mathrm{Y} ; \mathrm{R},-\mathrm{R})|\). This follows from the fact that, because of the alignment of the points, we know the values: \(\mathrm{R}-\mathrm{x}<\mathrm{R}+\mathrm{x}\) so their quotient is greater than 1 so positive logarithm and similarly for \(Y\). Since the natural logarithm function is strictly increasing:

\(|\ln (\mathrm{O}, \mathrm{X} ; \mathrm{R},-\mathrm{R})|=\ln (\mathrm{O}, \mathrm{X} ; \mathrm{R},-\mathrm{R})<\ln (\mathrm{O}, \mathrm{Y} ; \mathrm{R},-\mathrm{R})=|\ln (\mathrm{O}, \mathrm{Y} ; \mathrm{R},-\mathrm{R})|\). That is, \(\mathrm{d}_{\mathrm{p}}(\mathrm{O}, \mathrm{X})<\mathrm{d}_{\mathrm{p}}(\mathrm{O}, \mathrm{Y})\). Instead of the converse, it is easier to use this result to prove the inverse; in essence, what happens if \(x=y\) or if \(x>y\). In case \(x=y\), direct (trivial) computation confirms that \(d_{p}(O, X)=d_{p}(O, Y)\) and in case \(x>y\), we conclude \(d_{p}(O, X)>d_{p}(O, Y)\) by interchanging the roles of \(x\) and \(y\) in the preceding. QED.

Theorem: Poincaré line segments are congruent if and only if the reflection of an endpoint of each of them to the center of the defining circle (inversion in orthogonal circles) are congruent Euclidean segments.

Proof: This is an immediate consequence of the preceding Lemma and the fact that inversion in an orthogonal circle preserves cross ratio so that reflection in a Poincaré line preserves Poincaré measure. That is, two Poincaré segments are congruent if and only if their reflected images are congruent Poincaré segments and, since one endpoint of each reflected segment is the defining center, they are also Euclidean segments that are congruent Euclidean segments if and only if they are congruent Poincaré segments. QED.

Theorem: A Poincaré circle is (as a set) a Euclidean circle that stays entirely inside the Poincaré disc and its Poincaré center is collinear with the center of the defining circle and its Euclidean center.

Question: Wasn’t this the definition of Poincaré circle back in Chapter 3? Yes, but we "cheated". In neutral geometry (in which hyperbolic geometry is subsumed), the concept "circle" already has a standard definition so this can only be a model for hyperbolic geometry if the original "definition" is consistent with the real definition. We can prove that fact now that more sophistication has been developed.

Proof: Suppose \(C \in P\) and \(r>0\). By the (real) definition of circle, the Poincaré circle with center \(C\) and radius \(r\) is \((C ; r)_{\mathrm{P}}=\left\{X \in P \mid d_{P}(C, X)=r\right\}\). To prove that this set is a Euclidean circle, consider two cases:

i. \(C=O\), the center of the defining circle, or

ii. \(\mathrm{C} \neq \mathrm{O}\).

In the first case, Poincaré segments \(\mathrm{OX}\) for all \(\mathrm{X} \in \mathcal{P}\) are also Euclidean segments and line segments from \(\mathrm{O}\) are congruent as Poincaré segments if and only if they are congruent as Euclidean segments by the preceding Lemma. This implies that set \((O ; r)_{P}=\left\{X \in P \mid d_{P}(O, X)=r\right\}=\left\{X \in P \mid d(O, X)=r_{E}\right\}\), the Euclidean measure of the segment for some fixed real number \(\mathrm{r}_{\mathrm{E}}\). This is exactly the definition of the Euclidean circle \(\left(\mathrm{O} ; \mathrm{r}_{\mathrm{E}}\right)\) so that the original set of points, \((\mathrm{O} ; \mathrm{r})_{\mathrm{P}}\), is a Euclidean circle.

In the second case, reflect \(O\) in the unique Poincaré line \(\ell\) (inversion in the appropriate orthogonal circle) that carries C to O. Since reflection in \(\ell\) preserves distance, \(\left((C ; r)_{p}\right)^{\prime}=\left\{X^{\prime} \in P \mid d_{p}\left(C^{\prime}=O, X^{\prime}\right)=r\right\}\).

Since the \(X^{\prime}\) of this set contains all of the elements of \(P\), this set is exactly \(\left\{X \in P \mid d_{p}(O, X)=r\right\}\) and this set is exactly the definition of the Poincaré circle \((\mathrm{O} ; \mathrm{r})_{\mathrm{P}}\) that is, by case \(\mathrm{i}\), a Euclidean circle. Reflecting in \(\ell\) once again, the inverted set is inverted back onto the original set and, since the inversion of a circle in a circle is a circle or a line with a line being impossible here (the set is contained inside the defining circle so it cannot contain the center of the orthogonal circle of inversion) the original set is a Euclidean circle.

Conversely, suppose \(\delta\) is a Euclidean circle that is contained in the interior of \((\) that is not centered at \(O\), the center of the defining circle. Construct its Euclidean center \(\mathrm{C}_{\mathrm{E}}\) by the standard construction and let \(A\) and \(\mathrm{B}\) be the points of intersection of ray \(\mathrm{OC}_{\mathrm{E}}\) with \(\delta\) so that segment \(\mathrm{AB}\) is a diameter of the circle and also a Poincaré segment since it is collinear with \(\mathrm{O}\). Choose a \(3^{\text {rd }}\) point \(C \in \delta\) and construct the perpendicular bisector of the Poincaré segment \(\mathrm{AC}\) (or \(\mathrm{B}\) and \(\mathrm{C}\) ) (see \(\mathrm{PS} 5, \# 17\) ), identify the intersection with AB as \(\mathrm{C}_{\mathrm{P}}\) that is Poincaré equidistant from \(A\) and \(C\) (or \(B\) and \(C)\), and let \(r=d_{p}\left(C_{p}, C\right)\). The Euclidean reflection of the plane in the line will \(\mathrm{OC}_{\mathrm{E}}=\mathrm{OC}_{\mathrm{P}}\) is also a Poincaré reflection in the same line (Euclidean open diameter) identifies another point \(\mathrm{D} \in \delta\) for which \(\mathrm{C}_{\mathrm{P}}\) is also Poincaré equidistant from A (by symmetry of the situation with respect to diameter line \(\mathrm{OC}_{\mathrm{E}}\), see \(\mathrm{X}\) and \(\mathrm{Y}\) in the proof of #16). Now reflect \(\rho\) in the unique Poincaré line \(l\) (inversion in the appropriate orthogonal circle) that carries \(C_{p}\) to O. Since reflection in \(l\) preserves distance, \(\mathrm{O}\) is the same Poincaré distance \(r\) from \(\mathrm{A}^{\prime}, \mathrm{C}^{\prime}\), and \(\mathrm{D}^{\prime}\) on \(\delta^{\prime}\), the inversion of \(\delta\), that must be a Euclidean circle since it is the inversion of a Euclidean circle. Since \(\mathrm{OA}^{\prime}, \mathrm{OC}^{\prime}\), and \(\mathrm{OD}^{\prime}\) are \(\mathrm{Poincaré}^{\prime}\) congruent segments, they are also Euclidean congruent segments so \(\mathrm{A}^{\prime}, \mathrm{C}^{\prime}\), and \(\mathrm{D}^{\prime}\) are 3 distinct points on this Euclidean circle that are equidistant from \(\mathrm{O}=\left(\mathrm{C}_{\mathrm{P}}\right)^{\prime}\) so it is the center of circle \(\delta^{\prime}\). Reflecting in \(\ell\) once again, we have that \(\delta=\delta^{\prime \prime}\) is not only a Euclidean circle, it is the Poincaré circle \(\left(C_{p} ; r\right)_{\mathrm{P}}\). QED.

Theorem: Poincaré lines are straight.

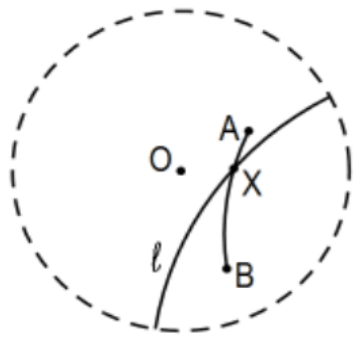
Proof: This tongue-in-cheek statement is an important theorem and is intended to point out the nebulous nature of "straightness". Our experience is so strong that we think we know until asked to describe what it means to be "straight" in mathematically defensible language. In formal terms, we do not try. Instead, the subsets we call lines have certain definitional properties that are never discussed in introductory courses (sometimes never!) and impose an axiom (Axiom 1) that two points determine exactly one of those sets. The actual definition of is any subset of the set of points (the plane) that separates the set into three mutually disjoint convex subsets, the set itself and two subsets (adjust analogously for "flatness" of a plane in space). This, of course, presupposes a notion of "convex" that itself depends on the notion of betweenness. A set is convex if, for any two points in the set, the set of all of the points between them is also in the set. In the language of geometry, if any two points are in the set, so is the line segment that they determine. That a Poincaré line, say \(l\), is itself convex is a consequence of an earlier result, \(\mathrm{PS} 3, \# 24\). The idea is that the concept of distance in neutral geometry must satisfy the strict form of the triangle inequality; i.e., for three distinct points \(A, B\), and \(C\), point \(B\) is between \(A\) and \(C\) iff \(d_{p}(A, B)+d_{p}(B, C)=d_{p}(A, C)\). That exercise only verified that the condition is satisfied for three collinear points in a Poincaré disk model. Any 3 (distinct) points is done below.

For t e other two sets determined by a Poincaré line, we prove the contrapositive. That is, if Poincaré line segment \(A B\) intersects a given line \(l\) where neither \(A\) nor \(B\) is in \(l\) (as pictured above), then the points are on opposite sides of \(l\). To that end, in the following Poincaré disk model, suppose \(\mathrm{X}\) is the intersection of segment \(A B\) and line \(l\). The figure seems to imply the desired result but that

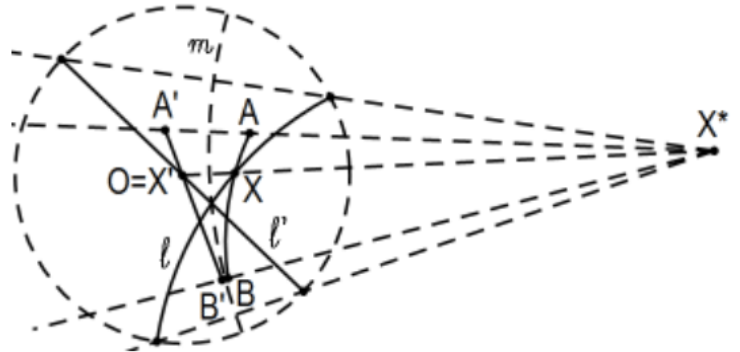
fact is a consequence of the proof; it is not a given. Let \(m\) be the Poincaré line in which \(\mathrm{X}\) is reflected onto \(\mathrm{O} ;\) i.e., \(\mathrm{O}=\mathrm{X}^{\prime}\) where this reflection means the inversion in the circle of which \(m\) is an arc that is orthogonal to the defining circle. The reflected lines \(l^{\prime}\) and \(\mathrm{A}^{\prime} \mathrm{B}^{\prime}\) are Euclidean lines and the Poincaré plane is divided into subsets of the two half-planes of the Euclidean plane determined by the Euclidean line of segment \(l^{\prime}\). Since \(A^{\prime} B^{\prime}\) is also a Euclidean segment with point \(O=X^{\prime}\) in the interior of the segment, "straightness" of Euclidean lines (i.e., convexity of both half planes) implies that \(A\) ’ and B’ lie on opposite sides of the Euclidean line \(\ell^{\prime}\). By properties of inversion in a circle, \(A\) and B must lie on opposite sides of \(l\).

There is another technicality that we should not overlook (along with many others that we will!): We need a nonnegative real valued distance function \(\mathrm{d}\) on a set \(\mathrm{S}\) to satisfy the triangle inequality property; for any three elements \(A, B\), and \(C\), it must be true that \(d_{p}(A, B)+d_{p}(B, C) \geq d_{p}(A, C)\). We need to check this condition for Poincaré distance. We already have this result for collinear points but we need it to be true in general. It is tempting to claim that, for non-collinear points, this is an immediate consequence of Proposition 20 of neutral geometry but that is rather complicated circular reasoning. The truth is that in assuming measure-based formal geometry (i.e. accepting Ruler and Protractor Postulates), that proposition was only proved herein for historical reasons. The fact is that the generalized inequality had to be true axiomatically so to be a valid model it has to be proved for the Poincaré plane (or any other model of a neutral geometry axiomatic system, hyperbolic or not).

Theorem: For three non-collinear points \(A, B\), and \(C\) in a Poincaré disk plane, \(\mathrm{d}_{\mathrm{p}}(\mathrm{A}, \mathrm{B})+\mathrm{d}_{\mathrm{p}}(\mathrm{B}, \mathrm{C})>\mathrm{d}_{\mathrm{p}}(\mathrm{A}, \mathrm{C})\)

Proof: Consider Poincaré \(\triangle \mathrm{ABC}\). For the following reason, it suffices to prove only the special case, that the hypotenuse of a right triangle is greater than either of its legs. By the construction of Ex 10, we can construct the perpendicular from B to line \(A C\), say \(F\) for the foot of the perpendicular. Assuming the right triangle case has been proved (the second figure), \(d_{p}(A, B)>d_{p}(A, F)\) and \(d_{p}(B, C)>d_{p}(F, C)\) so that \(d_{p}(A, B)+d_{p}(B, C)>d_{p}(A, F)+d_{p}(F, C)=d_{p}(A, C)\) in the case that \(F\) falls between \(A\) and \(C\) and \(d_{p}(A, F)+d_{p}(F, C)>d_{p}(A, C)\) if \(F\) falls outside Poincaré segment \(\mathrm{AC}\)

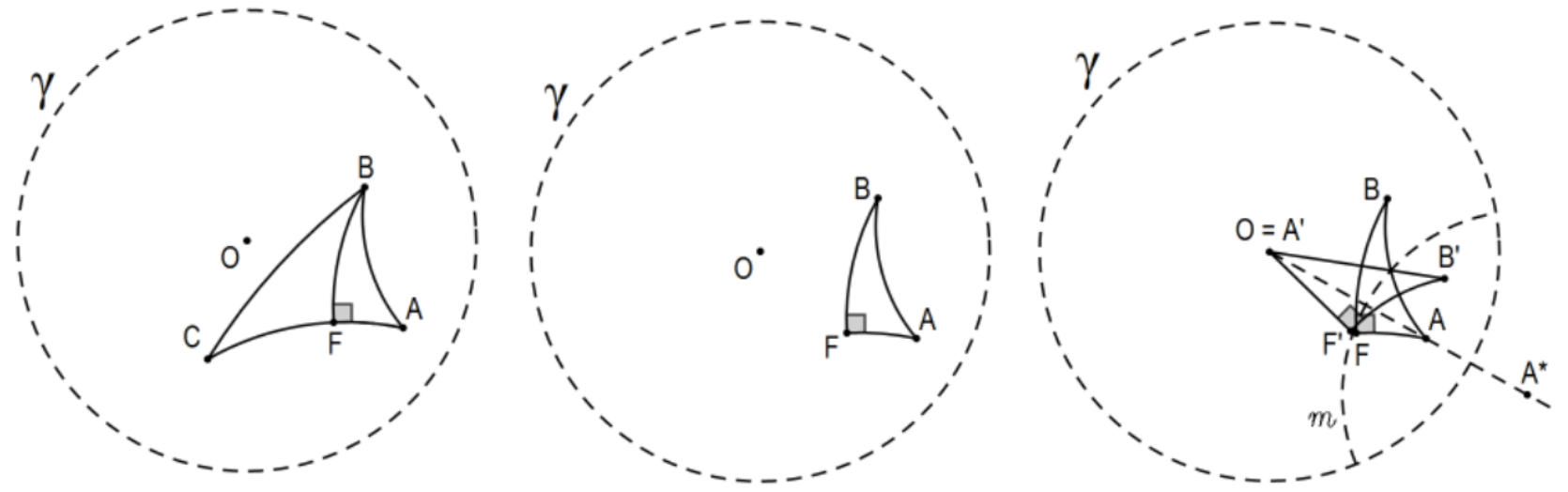
To prove \(\mathrm{d}_{\mathrm{p}}(\mathrm{A}, \mathrm{B})>\mathrm{d}_{\mathrm{p}}(\mathrm{A}, \mathrm{F})\) (and, by symmetry, \(\left.\mathrm{d}_{\mathrm{p}}(\mathrm{B}, \mathrm{C})>\mathrm{d}_{\mathrm{p}}(\mathrm{F}, \mathrm{C})\right)\), (Poincaré) reflect \(A\) onto \(\mathrm{O}\) in \(m\) (the third figure) the perpendicular bisector of Poincaré line segment \(A O\) (i.e., inversion in the appropriate Euclidean circle). This determines Poincaré \(\triangle \mathrm{OB}^{\prime} \mathrm{F}^{\prime} \cong \triangle \mathrm{ABF}\) so \(\mathrm{AB} \cong \mathrm{OB}, \mathrm{AF} \cong \mathrm{OF}^{\prime}\), and \(\angle \mathrm{OF}^{\prime} \mathrm{B}^{\prime} \cong \angle \mathrm{AFB}\) so that \(\angle \mathrm{OF}^{\prime} \mathrm{B}^{\prime}\) is a right angle. The desired result follows from \(\mathrm{PS} 5\), #8.

Theorem: SAS holds for the Poincaré model.

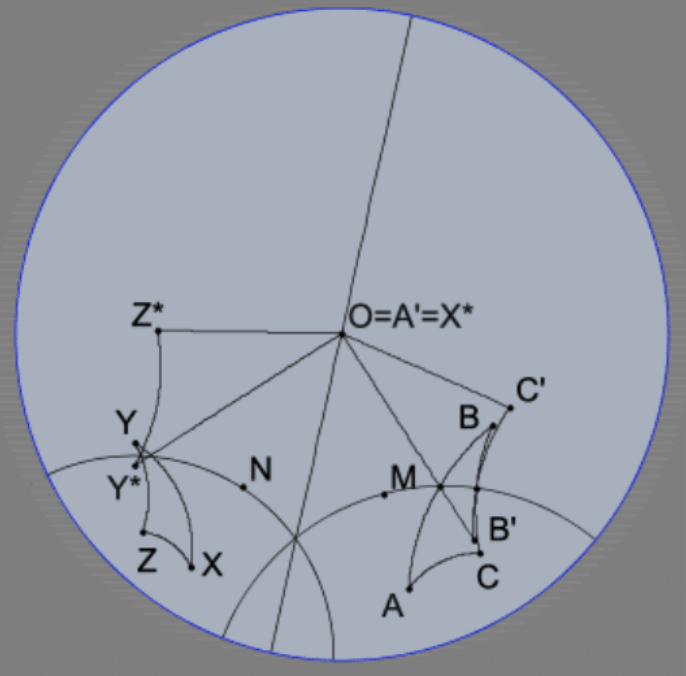
Proof: Suppose \(\triangle \mathrm{ABC}\) and \(\triangle \mathrm{XYZ}\) are Poincaré triangles that satisfy SAS as Poincaré triangles. Specifically, suppose that, with respect to Poincaré measure, \(\mathrm{AB} \cong \mathrm{XY}, \mathrm{AC} \cong \mathrm{XZ}\), and that their included angles are congruent, \(\angle \mathrm{A} \cong \angle \mathrm{X}\). Reflecting \(\mathrm{A}\) to \(\mathrm{O}\left(\mathrm{A}^{\prime}\right)\) and \(\mathrm{X}\) to \(\mathrm{O}\left(\mathrm{X}^{*}\right)\), the reflections in the (Poincaré) perpendicular bisectors of segments \(\mathrm{AO}\) and XO respectively; i.e., the indicated lines through their (Poincaré) midpoints, \(M\) and \(N\). The reflections of the triangles preserves their Poincaré lengths and angle measures so that \(\triangle \mathrm{ABC} \cong \triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime}\) and \(\triangle \mathrm{XYZ} \cong \triangle \mathrm{X}^{*} \mathrm{Y}^{*} \mathrm{Z}^{*}\left(\right.\) with \(\mathrm{O}=\mathrm{A}^{\prime}=\mathrm{X}^{*}\) ) so these new triangles satisfy the same Poincaré conditions as do the originals; i.e, \(\mathrm{OB}^{\prime} \cong \mathrm{OY}^{*}\) and \(\mathrm{OC}^{\prime} \cong \mathrm{OZ}^{*}\) (as Poincaré segments) and their included angles at \(\mathrm{O}\) are also congruent.

By the preceding theorem, however, these transformed segments ( since they are radii of the defining circle) are also congruent as Euclidean segments so that the Euclidean triangles they determine are congruent, \(\triangle \mathrm{OB}^{\prime} \mathrm{C}^{\prime} \cong \triangle \mathrm{OY} * \mathrm{Z}^{*}\), by the \(\mathrm{SAS}\) Axiom. Now either a flip (inversion) in a diameter (as pictured) or a rotation around \(\mathrm{O}\) carries one Euclidean triangle \(\Delta \mathrm{OB}^{\prime} \mathrm{C}^{\prime}\) onto the other, \(\Delta \mathrm{OX}^{*} \mathrm{Y}^{*}\). This last inversion is a Poincaré congruence as well as Euclidean since the Poincaré lengths and angles are preserved for the two sides from \(\mathrm{O}\) and their included angle leaving only their third (Poincaré) side and other two angles. These must coincide as well because (by Axiom 1 ) these other two points determine a unique Poincaré line which determines the Poincaré side in question. Similar remarks apply to the angles these arcs determine with the two radial sides. By symmetry and transitivity (i.e., composition), the original \(\triangle \mathrm{ABC}\) and \(\triangle \mathrm{XYZ}\) are congruent as Poincaré triangles. QED.

Theorem: The Poincaré model is a model for hyperbolic geometry.

Proof: We would first have to make precise all of the rest of those unspecified axioms and then prove them. No thanks.

M. C. Escher was an artist who expressed his intrigue with unusual perspectives that offers insight into inversions in circles and the Poincaré disk model for hyperbolic geometry. One of his more famous is this Self Portrait in a Spherical Mirror. It is a three-dimensional analog of the two-dimensional situation that we have been studying, inversion of the Euclidean plane in a circle. As is always the case with a mirror, reflection in a mirror is not quite the mathematical equivalent because it only an illusion. A perfect mirror does actually reflect each point in 3-space to the point on the opposite side such that the mirror is the plane that is the perpendicular bisector of the segment determined by the point and its image; it just looks that way. Obviously, points on the reverse side of the mirror are not part of the scene at all. In the spherical case of this artwork, points outside of the sphere appear to be inside (although obviously they are not) and points inside are not part of the scene at all so the situation is not a transformation all of the is "punctured" three-dimensional Euclidean space but is still highly suggestive of it. The plane situation we have been studying would be that of each plane through the center of the sphere and the inversion of the region outside of the circle of intersection in that circle. [www.freakingnews.com/ Escher-Hand-with-Reflecting-Sphere-in-Color-Pics-50737.asp - Used without permission.]

M.C. Escher’s "Circle limit IV".

All M.C. Escher works

Cordon Art - Baarn - Holland

plus.maths.org/content/os/issue18/xfile/index All rights reserved.

H.S.M. Coxeter’s tessellation of the

Poincaré plane with congruent 30-45-90 triangles

(or isosceles \(60-45-45\) triangles)

mathaware.org/mam/03/essay1.html

All rights reserved.

Finally, why "Hyperbolic" Geometry and what is its connection with the Poincaré model? From this cover of a wonderful book on the history of Hyperbolic Geometry, identify corresponding points of an elliptic hyperboloid using the Poincaré model as a guide: Sources of Hyperbolic Geometry, John Stillwell. A co-publication of the AMS and the London Mathematical Society, History of Math, Vol: 10, \(1996 .\) Cover picture reproduced with permission of Dr. Konrad Polthier.