5.2: Problem Set 5

Unless otherwise stated, assume all of the axioms of neutral geometry (albeit unstated) and the global form of the Euclidean Parallel Postulate as well.

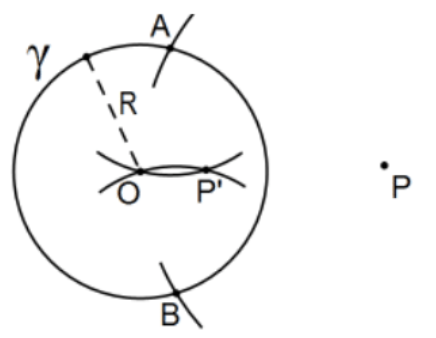
1. Prove that the following alternate construction of the inversion of a given point outside of a given circle in the circle is valid. Don’t forget to confirm that \(\mathrm{P}^{\prime}\) is on ray OP.

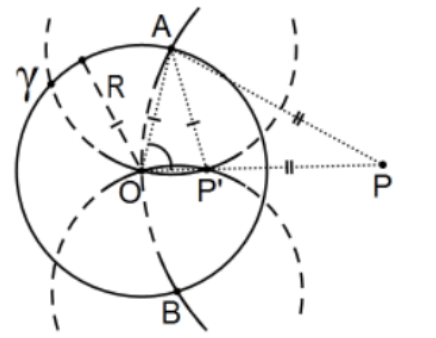
Construction: Given the circle \(\gamma=(\mathrm{O}\); R) (i.e., centered at \(\mathrm{O}\) of radius R) and \(\mathrm{P}\) outside of the circle, let \(\mathrm{A}\) and \(\mathrm{B}\) be determined by circle (P; OP) and let \(\mathrm{P}^{\prime}\) be determined by the other intersection of circles (A; AO) and (B; BO). Then \(\mathrm{P}^{\prime}\) is the desired inversion of \(\mathrm{P}\) in the given circle \(\gamma\).

[Hint: First show that \(\mathrm{O}, \mathrm{P}\), and \(\mathrm{P}^{\prime}\) are collinear (think of segment \(\mathrm{AB}\) ).]

Why is this not a theorem in neutral geometry? That is, all the steps of this construction can be made in neutral geometry so why restrict to Euclidean?

Note: The dotted line segments in the second sketch construction were not part of the construction; they are only there to emphasize their existence part of the proof. The significance of this is that this construction was made using compass only. An amazing theorem of Euclidean geometry (Mohr-Mascheroni) is that every possible straightedge and compass construction can be done without the straightedge! That is, although two points determine a line, the line itself need not be a part of the next stage of the construction using some alternate procedure. To get an idea of what this means (and how tricky things are), consider trying to construct the intersection of two lines, each given by only two points for each line without actually drawing the lines. The solution involves the fact that the inversion of the intersecting lines in an appropriate circle are intersecting circles with one intersection at the center of the circle of inversion and the other being the inversion of the intersection of the original lines that can be constructed because all of these can be done with only a compass. Finally, the inversion of that point of intersection of the circles is the desired intersection.

The process just described requires the ability to do inversions of all points, not just those outside of the circle as with Ex 1. Here is how that can be done: Exactly the same proof works if \(P\) is inside the circle but more than halfway "out"; that is, \(\mathrm{OP}>\mathrm{R} / 2\). With a slight modification, this works for any \(\mathrm{P} \neq \mathrm{O}\). The idea rests on the fact that there is a trivial circles only construction to double a line segment and, by extension, any number of times the segment along the same line; i.e., collinear with the original 2 points. The idea is to use the compass at one of the points, construct the circle with that segment as its radius, and then "walk halfway around the circle with the same radius" as with the trivial construction of a regular hexagon. That point, say \(\mathrm{P}_{2}\), is diametrically opposed to \(\mathrm{O}\) through \(\mathrm{P}\) and hence collinear with them doubling of length of segment OP. Repeating the process, gives any number \(n\) of equally spaced collinear points. Use of the inversion technique rests on proving that if \(P_{n}\) is the point such that \(\mathrm{OP}_{n}=n(O P)\), then inverting \(P_{n}\) to obtain \(P_{n}{ }^{\prime}\), then \(n\left(O O P_{n}{ }^{\prime}\right)=P^{\prime}\), the inversion of the original \(P\). In the algebra, the proof rests on the fact that if \(0<x<R\), then \(0<(R-x)^{2}\).

2. Almost by definition, if two circles are orthogonal, the center of either is exterior to the other (see Note 2 immediately following the description of Poincaré lines in Chapter 3). By the Fundamental Theorem of Orthogonal Circles, we can say much more. Prove that two intersecting circles are orthogonal if and only if a point \(\mathrm{P}\) on one of them that is in the interior of the other has its center on the perpendicular bisector of the line segment \(\mathrm{PP}^{\prime}\) where \(\mathrm{P}^{\prime}\) is the inversion of \(\mathrm{P}\) in the circle containing \(\mathrm{P}\) in its interior.

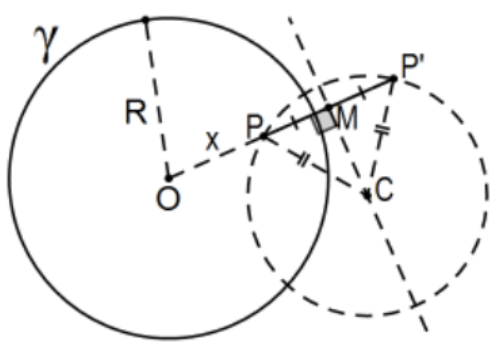
Note: The proof of #2 is very easy but it is interesting to calculate exactly where that perpendicular bisector is in relation to the position of \(\mathrm{P}\) and the radius of the circle. That is, calculate the position of the midpoint of the line segment as a function of \(x=m(O P)\) and \(R\) in this figure, the center of the circle (orthogonal) with diameter \(\mathrm{PP}^{\prime}\).

3. Let \(A\) and \(B\) be two points in the interior of circle \(\gamma\) centered at \(O\) that are not collinear with \(O\) in the Poincaré model determined by Euclidean circle \(\gamma\). Construct Poincaré line segment AB.

4. Starting with the result of #3, construct the isometric inversion (i.e., congruence) of the Poincaré model onto itself that carries \(A\) to \(\mathrm{O}\); i.e., \(\mathrm{A}^{\prime}=\mathrm{O}\) and the Poincaré line segment \(\mathrm{A}^{\prime} \mathrm{B}^{\prime}=\mathrm{OB}^{\prime}\), the \((\mathrm{Poincaré}\) congruent) image of segment \(A B\) thus determined.
5. Starting with the result of #4, prove that the Poincaré length of segment \(A B\) is simply \(\ln \left(\frac{R+X}{R-X}\right)\) where \(x\) is the Euclidean length of segment \(\mathrm{OB}^{\prime}\).

Note: Approximate measures can be determined by direct measurement (and this final computation) but in theoretical geometry, direct measurement “doesn’t count.” All angle, line segment, area, and volume “measures" are not really measures at all; they are infinitely accurate numerical values - an impossibility with direct measurement. Use of this in the \(\mathrm{x}, \mathrm{y}\)-plane (given radius \(\mathrm{R}\) and given the coordinates of interior points \(A\) and B) can yield the theoretically precise value of \(x\) as a function of the coordinates of \(A\) and \(B\) so the theoretically precise value of the Poincaré length of the determined segment AB. This is developed in the Solutions Manual along with a numerical example.

6. Continuing with #4, let \(\mathrm{C} \neq \mathrm{O}\) be a third point in the interior of \(\gamma\) that is not collinear (in the Poincaré sense) with A and B. Sketch in (or carefully construct) Poincaré segments AC and BC to obtain Poincaré triangle \(\triangle \mathrm{ABC}\) and complete the congruence (isometric \(=\) distance preserving and angle preserving) transformation of the Poincaré model onto itself that carries \(\mathrm{A}\) to \(\mathrm{O}\); i.e., \(\mathrm{A}^{\prime}=\mathrm{O}\) and carefully sketch \(\triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime}\) the image of triangle \(\triangle \mathrm{ABC}\) thus determined. [Note: This is the basic construction in the proof of SAS for the Poincaré disk model.]

7. Prove that, in the Cartesian plane, the circle of radius 2 centered at the origin and the circle of radius \(3 / 2\) centered at \((5 / 2,0)\) are orthogonal. Know at least three different solutions but the easiest is that \((1)(4)=2^{2}\). Why is that fact sufficient?
8. Complete the proof of the triangle inequality of Poincaré measure in the non-collinear case (strict inequality) by completing the proof indicated in this figure that the hypotenuse of a Poincaré right triangle with one acute angle vertex at the center of the defining circle is greater than the leg with one endpoint at the center. [Hint: Consider the lemma that, for two Poincaré segments each with an endpoint at the center of the defining circle, the Poincaré length of one is greater than the other if and only if the same inequality is true for their Euclidean lengths (measures).

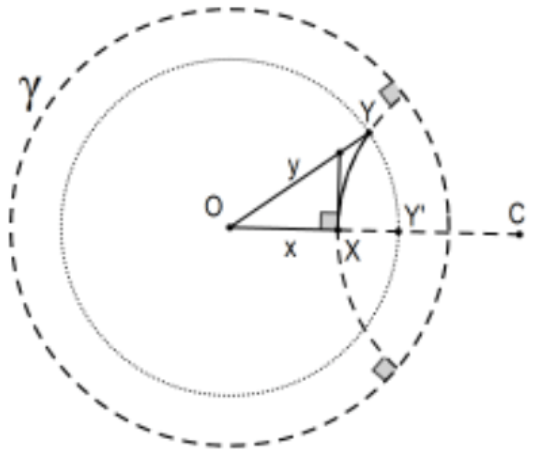
Note: For readers who know a little topology, the combination of the collinear and noncollinear cases complete verification of the general triangle inequality needed to complete verification that the distance of the Poincaré model makes it a metric space. Beyond that, distance from the common \(\mathrm{O}\) along radii (use polar coordinates with the same angle for the x, y plane with defining circle centered at the origin) is a homomorphism of the Poincaré disk to the x,y plane. More explicitly:

Let \(\sigma\) be the Poincaré disk model centered at \(\mathrm{O}\) where the model of the Euclidean \(\varepsilon\) is the \(\mathrm{r}, \theta\) plane: \(f: \otimes \rightarrow \varepsilon\) via \(f(\mathrm{r}, \theta)=\left(\mathrm{d}_{f}(\mathrm{O},(\mathrm{r}, \theta)), \theta\right)\) is a homomorphism; i.e., topologically, exactly the same.

9. Give an analytic proof that the inversion of a circle that does not contain the center of the circle of inversion is a circle. [Note: I have never done this without complex analysis but I believe that it must work!]

10. Prove Case iv b of the "Lines and Circles Theorem".

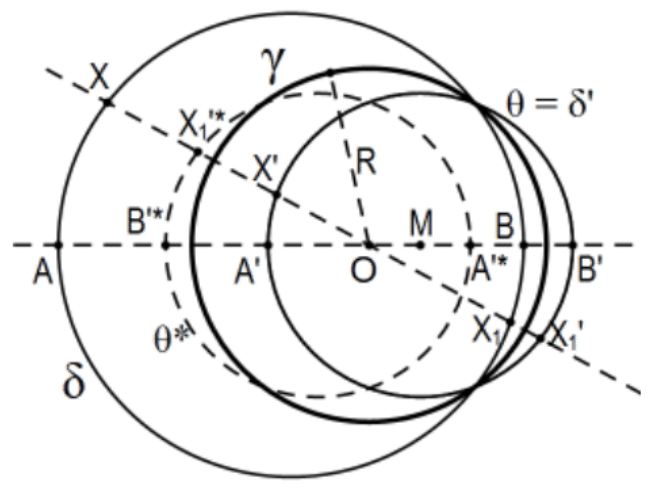
The idea is that the equation of Part a is still valid but the resulting inversion is not a dilation in the usual sense but it is close. If one extends dilation to include negative multipliers; i.e., opposite vectors, the proof is exactly the same. For the usual idea of dilation, take the opposite of each, \(X^{\prime *}\), the dashed circle instead of the inversion itself. In fact, using "negative length" when the direction of a segment along a line is reversed, the fact that \(\mathrm{O}\) is between \(\mathrm{A}\) and \(\mathrm{B}\) implies the change of sign so the negativity of the multiplier \(\mathrm{R}^{2} /(\mathrm{OA})(\mathrm{OB})\).

11. Analogous to tessellations of the Poincaré disk with infinitely many congruent triangles, a sphere (our real-world) can easily be tessellated with finitely many ones. As with hyperbolic geometry, there is an AAA congruency theorem in spherical geometry (if triangles are not too big). Probably the easiest is to consider the northern hemisphere (equator to the north pole) and, at the north pole, consider 4 longitudinal lines at \(90^{\circ}\) intervals \(-0^{\circ}, 90^{\circ}, 180^{\circ}\), and \(270^{\circ}\). The result is eight \(90^{\circ}-90^{\circ}-90^{\circ}\) congruent triangles covering the entire sphere. Here are some others. Find the size of the vertex angles of each single-colored triangle. [Hint: Look at all of the vertices that come together to make \(360^{\circ}\).]

Geometries, A.B. Sossinsky, AMS Student Mathematical Library No. 64, \(2012 .\) From the cover and used without permission.

Euclidean constructions of Poincaré Disk points and lines

It should not come as any great surprise that any constructible geometric figure in neutral geometry (i.e., with abstractions of a straightedge and compass) can be constructed in the Poincaré disk model for hyperbolic geometry using strictly Euclidean constructions. Some of these we have already done and some are given here complete with proof to help get the "feel"of how this works. Finally, there are some with at most hints as how to begin. In the following, assume the Poincaré plane is \(\theta\) determined by circle \(\gamma\) centered at O. Prerequisite Euclidean constructions are assumed so the details will be omitted unless they seem particularly helpful or needed:

The circle determined by three noncollinear points.

The tangent to a circle at a point on it.

The tangents to a circle from a point outside of it.

The inversion in a circle of a point inside or outside the circle.

12. The Poincaré line perpendicular to a Poincaré line \(\ell\) on a point \(P\) (whether or not \(P \in \ell\) ).

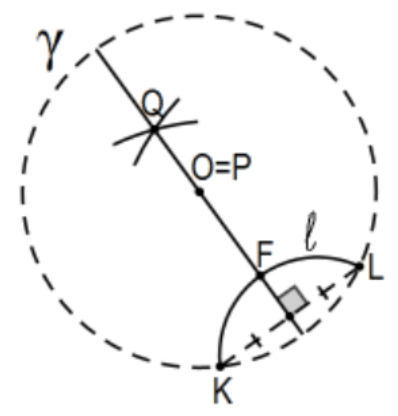
Two cases occur:

Let \(\mathrm{K}\) and \(\mathrm{L}\) be the intersections of the Euclidean circle of the Poincaré line \(\ell\) with the defining circle \(\gamma\) with center at \(\mathrm{O}\).

Case 1: \(\mathrm{P}\) is equidistant from \(\mathrm{K}\) and \(\mathrm{L}\), or

Case 2: P is not equidistant from \(\mathrm{K}\) and \(\mathrm{L}\).

Case 1: \(P\) is equidistant from \(\mathrm{K}\) and \(\mathrm{L}\) and so is \(\mathrm{O}\) (radii of the defining circle) so line \(\mathrm{OP}\) is the perpendicular bisector of segment KL unless \(\mathrm{P}=\mathrm{O}\) (figure) in which case construct Q, another point equidistant from \(K\) and \(L\). Then line \(P Q=O Q\) is the perpendicular bisector of segment KL. Line \(P Q=O Q\) is the desired Poincaré perpendicular to line \(\ell\).

Proof: Let \(\mathrm{F}\) be the intersection of this line with \(\ell\). We need to know that line PQ is the Poincaré perpendicular to Poincaré line \(\ell\) but (by the definition of Poincaré angle measure) that is if and only if it is perpendicular to the Euclidean tangent at point F. However, we get this "for free" because segment KL he is also a chord of the Euclidean circle that determines Poincaré line \(\ell\) so that its center, say C, is equidistant from \(\mathrm{K}\) and \(\mathrm{L}\) so \(\mathrm{C}\) also lies on the line OP. Therefore the Euclidean perpendicular at \(\mathrm{F}\) is perpendicular to the radius FC and, by the standard theorem, this perpendicular line is the Euclidean tangent to that circle.

Case 2: Let \(\mathrm{P}^{\prime}\) be the inversion of \(\mathrm{P}\) in \(\gamma\) and let \(C\) be determined as the intersection of the perpendicular bisector of segment \(\mathrm{PP}^{\prime}\) with line KL since they must intersect. Then the desired Poincaré line is the open arc of the indicated circle \(\delta=(C ; C P)\). In case \(P \in l\), the situation is exactly the same and we would conclude that \(\mathrm{F}=\mathrm{P}\).

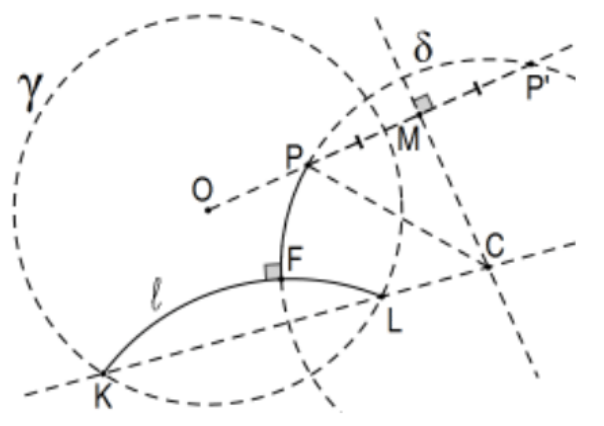
Proof: Orthogonality of \(\delta\) with \(\gamma\) is immediate from the Fundamental Theorem of Orthogonal Circles since ray OP also contains \(\mathrm{P}^{\prime}\), the inversion of \(P\) in \(\gamma\). By definition of Poincaré line, the defining circle of Poincaré line \(\ell\) is also orthogonal to \(\gamma\) and ray CL also contains \(K\). Again by the Fundamental Theorem of Orthogonal Circles, the circle of Poincaré line \(\ell\) is also orthogonal to \(\delta\). That is, the Poincaré line on \(P\) determined by orthogonal (with \(\gamma\) ) circle \(\delta\) is the desired Poincaré perpendicular to \(\ell\) and the indicated point \(F\) is the foot F of the Poincaré perpendicular. Amazingly, we have everything we need almost for free!

13. The common perpendicular to two non-boundary parallel lines:

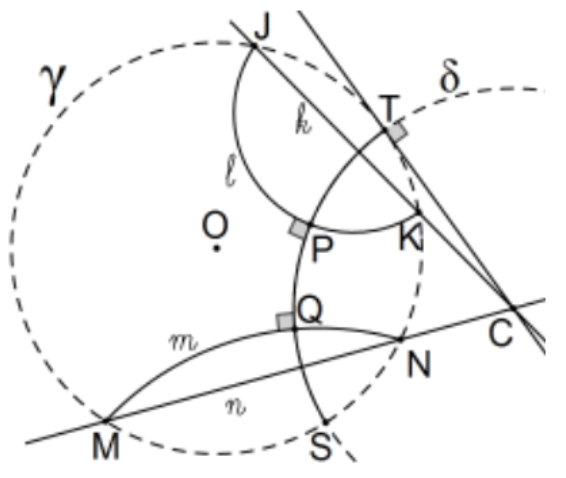
Let \(l\) and \(m\) be Poincaré lines and \(k\) and \(n\) be the Euclidean lines of the chords of the Euclidean circles (or line) determined by \(l\) and \(m\), respectively, with \(\gamma\). If \(k\) and \(n\) do not intersect, that is, they are Euclidean parallel, the line is the diameter of common perpendicular bisectors of the chords. If \(k\) and \(n\) intersect, say \(\mathrm{C}\), this is the center of the desired circle and the point of tangency from it to any of the Euclidean circle arcs \(\gamma, l\), or \(m\), e.g., \(\mathrm{T}\), determines the radius so \(\delta=(\mathrm{C} ; \mathrm{CT})\) determines the desired Poincaré line \(\mathrm{PQ}\).

Proof: Since Euclidean line CT is tangent to \(\gamma\), the new circle is orthogonal so that a Poincaré line is determined. Orthogonality with \(l\) and \(m\) is immediate as in Ex. \(12 .\)

14. The boundary parallels to line \(l\) on point \(\mathbf{p}\) not on \(\ell\) :

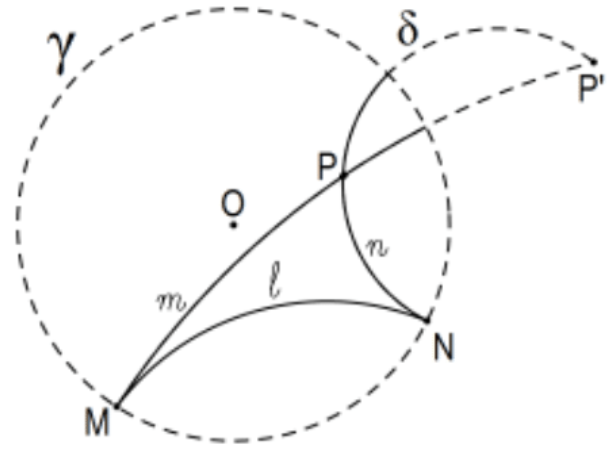
Case 1: If \(\mathrm{P}=\mathrm{O}\), the desired lines are the obvious diameters.

Case 2: \(P \neq O\), let \(\mathrm{P}^{\prime}\) be the inversion \(\mathrm{P}\) in \(\gamma\) to obtain \(\mathrm{P}^{\prime}\).

Let \(M\), and \(N\) be the points determined by the extension (Euclidean circle or line) of \(\ell\) with \(\gamma\). The Euclidean circles (i.e., Poincaré lines) are the ones determined by \(\mathrm{P}, \mathrm{P}^{\prime}\), and \(\mathrm{M}\) or \(\mathrm{N}\).

Note: This is the same construction as that of the Poincaré line determined by two Poincaré points except that one of them is now a boundary point instead of one of the interior points.

15. The perpendicular bisector of a Poincaré line segment:

Let \(A\) and \(B\) be the endpoints of the given Poincaré segment:

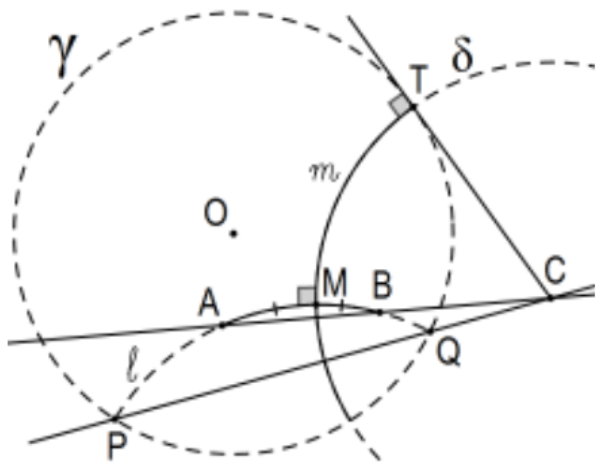
Case 1: \(\mathrm{OA} \cong \mathrm{OB}\). Trivial; it is the perpendicular bisector of Euclidean chord AB. (No point \(C\) in the figure.)

Case 2: \(\mathrm{A}, \mathrm{B}\), and \(\mathrm{O}\) collinear. In this case, Poincaré segment \(\mathrm{AB}\) is the same set as Euclidean segment \(A B\) and the Poincaré circle with diameter \(\mathrm{AB}\) is the same set as the Euclidean circle with the same diameter so first construct the Euclidean circle with that diameter (midpoint and...) and finally its Poincaré center (Ex 17).

Case 3: A, B, and \(\mathrm{O}\) non-collinear. Euclidean lines \(\mathrm{AB}\) and \(\mathrm{PQ}\) are not parallel (that was Case 1) so let \(C\) be their intersection. Proceed as indicated.

16. The Poincaré line of reflection (i.e., Euclidean circle of inversion) that carries a given point to another given point: This generalizes the important special case of reflecting a point to the center of the defining circle. [Hint: Exactly Ex. 15, A to B or equivalently, B to A.]

17. The Poincaré center of a Poincaré circle:

A natural but tedious solution is to use Ex. 14 and follow the standard (neutral geometry) construction. That is, choose any four points (or three is more common) to determine two Poincaré chords with the center being the intersection of the Poincaré circles. A much easier solution is to "cheat" by first constructing its Euclidean center and, by using the line of centers to be one of the perpendicular bisectors, we can get by with only one chord.

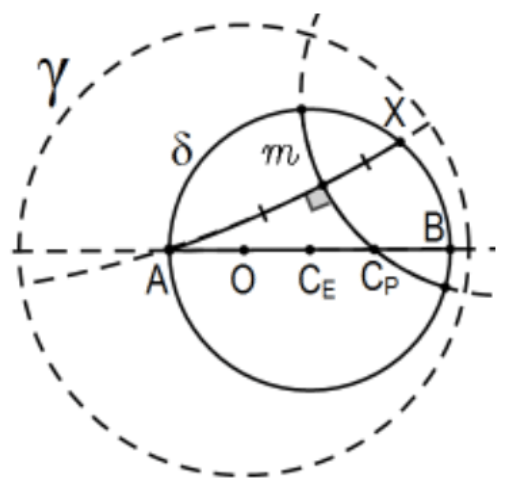
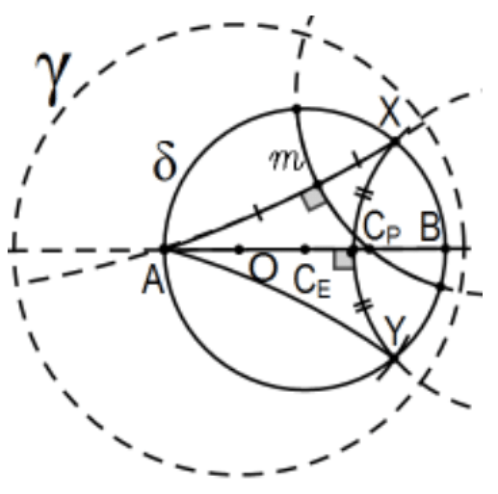
Construction: Let \(\mathrm{O}\) be the center of the defining circle \(\gamma\) and let \(C_{E}\) be the Euclidean center of the Poincaré circle. If \(O=C_{E}\), we are done so assume they determine a line and let \(\mathrm{A}\) and \(\mathrm{B}\) be its intersections with the circle in question. Let \(\mathrm{X}\) be any other point of circle. Construct the Poincaré line determined by A and X and the perpendicular bisector \(m\) of the Poincaré segment \(\mathrm{AX}\) (Ex. 15). The intersection of \(m\) and diameter \(\mathrm{AB}, \mathrm{C}_{\mathrm{P}}\), is the Poincaré center of the circle. The second construction is the same but using BX instead of AX. As described in the proof below, there is a practical advantage when the points A and B are so positioned.

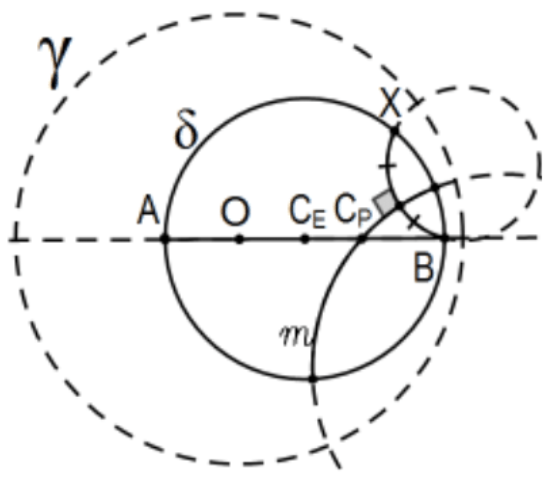
Proof: The fact that the Poincaré center is on the diameter of Euclidean centers will be a consequence of the proof and is based on carefully choosing the 3 points for 2 Poincaré chords of which the Poincaré perpendicular bisectors are to intersect to determine the center by neutral geometry considerations. The idea is to use \(X\) and \(A\) (or B) to determine one of the chords and Euclidean segment \(\mathrm{OX}\) (or \(\mathrm{AX}\) or \(B X\) ) to swing an arc to establish \(Y\) as the Euclidean reflection of \(X\) in the line of centers. Entirely by symmetry, the Poincaré perpendicular bisector of Poincaré chord AY (or BY)must intersect at the same point, \(C_{p}\).

\(\underline{\text { Note 1: }}\) The construction of the Poincaré line AX is particularly messy because it is so close to \(\mathrm{O}\) that the center of the Euclidean circle of the Poincaré line is far off the page so difficult to physically construct with Euclidean tools or even to really see (in a practical sense, not theoretical) the location of its center. Choosing BX instead makes it much clearer.

\(\underline{\text { Note 2: This construction can be used to construct the Poincaré midpoint of a line segment AB when A and }\) \(\mathrm{B}\) are collinear with \(\mathrm{O}\). The idea is to construct its Euclidean midpoint and the Euclidean circle with diameter AB. Finally, choose any other point \(X\) on the circle, and follow the same construction. Then \(C_{p}\) is the Poincaré midpoint of AB.

18. The Circle given its Poincaré Center and Radius:

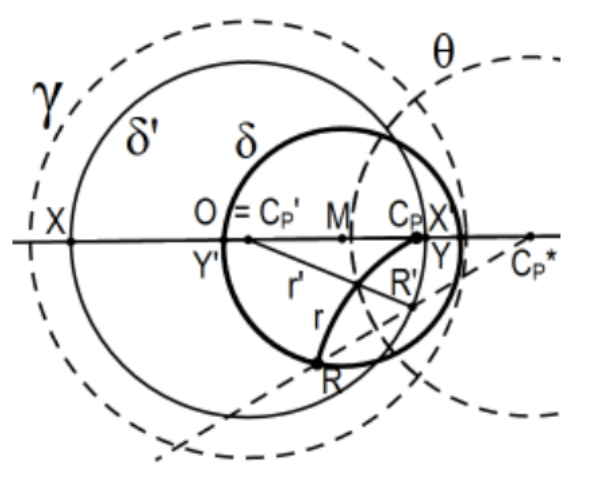
Construction: Let \(\mathrm{O}\) be the center of the defining circle \(\boldsymbol{\gamma}\) and let \(C_{\mathrm{p}}\) be the Poincaré center and Poincaré segment \(C_{\mathrm{p}} \mathrm{R}=\mathrm{r}\) be the radius of the Poincaré circle determined \(\delta=\left(C_{\mathrm{p}} ; \mathrm{C}_{\mathrm{p}} \mathrm{R}\right)\) to be constructed using Euclidean tools, all indicated in bold. First, construct \(\theta\), inversion in which carries \(C_{p}\) to \(O, O=C_{p}{ }^{\prime}\). It also carries \(\mathrm{R}\) to \(\mathrm{R}^{\prime}\) that must lie on \(\delta^{\prime}\), the inversion of \(\delta\) in \(\theta\). construction of \(\delta^{\prime}=\left(\mathrm{O} ; \mathrm{OR}^{\prime}\right)=\left(\mathrm{O} ; \mathrm{r}^{\prime}\right)\) is a triviality and, letting \(\mathrm{X}\) and \(\mathrm{Y}\) be the intersections of \(\delta^{\prime}\), we have a diameter, the inversion of which in \(\theta, X^{\prime}\) and \(Y^{\prime}\), must be a diameter of the desired circle \(\delta\). We now have two ways to finish the construction, either use the 3 points of \(\delta\) knowing that it is a Euclidean circle \(X^{\prime}\), \(Y^{\prime}\), and \(R\), or construct the Euclidean midpoint \(M\) of segment \(X^{\prime} Y^{\prime}\) and we have \(\delta=(M\), \(\left.M^{\prime}\right)=\left(M, M^{\prime}\right)\)

19. Theorem: A set of Poincaré points is a Poincaré circle if and only if it is a Euclidean circle that lies entirely inside the defining circle.

20. The Poincaré Bisector of a Poincaré Angle:

Here are two solutions. Reflect the vertex to the center and follow a point on each ray... Or construct the Euclidean tangents to each Poincaré line at the vertex and bisect the resulting Euclidean angle. Finally, construct the orthogonal circle through that point and tangent to the angle bisector.

Note: Once you get a feel for how this goes, more complicated ones are not so hard but even copying a line segment or an angle is more involved than you might think but are absolutely critical to the proof that the Poincaré Disk is a model for hyperbolic geometry. Here is an example:

21. The Tangents to a Poincaré Circle P outside the Circle:

The most obvious solution is to follow the neutral geometry construction (PS 2, #25 as pictured in PS 3, #25) since each of the needed Euclidean constructions has now been presented. Another approach is the idea of inverting a critical point to \(\mathrm{O}\), doing the work, and then inverting back, a common technique that has been used before (e.g., SAS).

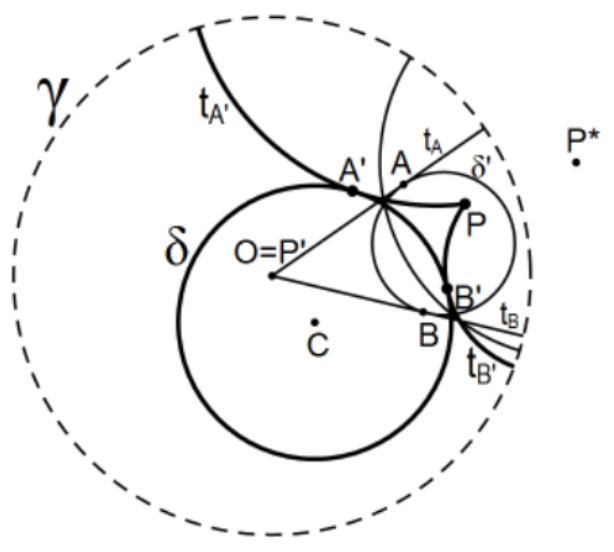
The idea is to choose the critical point to map to the center of the defining circle by inversion in an appropriate Poincaré line. Let the circle be the one with Poincaré center C (C is not used in the Euclidean construction - see details below) and P be the point from which the tangents are to be constructed and the appropriate Poincaré line is the one centered at the inversion of \(P\) in the defining circle, say \(\mathrm{P}^{*}\) (not pictured here) so as not to confuse it with inversions in this new circle) with radius determined by the Euclidean *perpendicular at \(\mathrm{P}\) to ray \(\mathrm{OP}\) where \(\mathrm{O}\) is the center of the defining circle. This circle determines, the arc through \(\mathrm{M}\), the Poincaré perpendicular bisector of line segment OP, the line that reflects \(P\) to O. Reflecting the circle in this line(that is, inversion in this Euclidean circle), its reflection will be another circle but, this time, the point in question is the center of the defining circle so that its Euclidean tangents are also its Poincaré tangents, points \(A\) and \(B\) in. the figure. Inverting \(A\) and \(B\) in the same line we obtain the points of tangency, \(\mathrm{A}^{\prime}\) and \(\mathrm{B}^{\prime}\). Using \(\mathrm{P}^{*}\), we have three points to construct each of the needed orthogonal Euclidean circles; i.e., each of the circles determined by \(\mathrm{P}^{\prime} \mathrm{A}^{\prime}\), and \(\mathrm{P}^{*}\) and \(\mathrm{P}, \mathrm{B}^{\prime}\), and \(\mathrm{P}^{*}\). These arcs are the desired tangents since they preserve orthogonality with the Poincaré radii at \(A\) and B.

Actually doing this without the assistance of Cinderella, even with the assistance of Geometer’s Sketchpad, gets kind of messy: As the last exercise in Chapter 4, we start with \(\alpha\), a circle that contains \(O\), the center of the defining circle just to show how the center gets inverted outside as \(P\) gets inverted to \(O\). How to do that? Let C be its Euclidean center (instead of its Poincaré center in the picture above) and consider points X and \(\mathrm{Y}\) (not pictured) determined by the ray \(\mathrm{P} * \mathrm{C}\), a Euclidean diameter of the circle. Invert \(\mathrm{X}\) and \(\mathrm{Y}\) in the inverting circle to obtain \(\mathrm{X}^{\prime}\) and \(\mathrm{Y}^{\prime}\) that must be a diameter of the inverted circle. Now the Euclidean midpoint \(M\) of segment \(\mathrm{X}^{\prime} \mathrm{Y}^{\prime}\) with either point for the radius determines the complete inverted circle \(\alpha^{\prime}\). The Poincaré tangents from \(\mathrm{O}=\mathrm{P}^{\prime}\) to this new circle are exactly the same as the Euclidean ones so determine the Euclidean tangent points \(A\) and \(B\) of the inverted circle. These are also the Poincaré tangent points so invert them back to the original circle \(A^{\prime}\) and \(B^{\prime}\). The Euclidean circles determined by \(P, A^{\prime}\), and \(P^{*}\) and \(P\), \(\mathrm{B}^{\prime}\), and \(\mathrm{P}^{*}\) determine the desired Poincaré tangent lines.

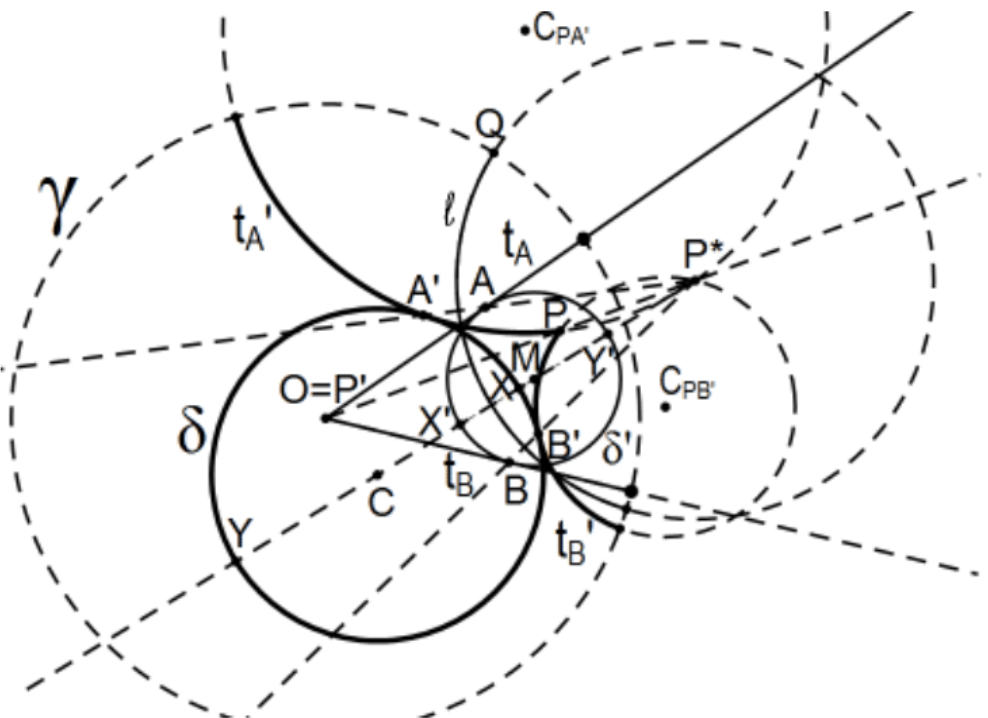
Confusing, no? In the above, the defining circle is the large circle \(\gamma\) on the left with center \(\mathrm{O}\) and the given circle is the larger circle \(\alpha\) that contains \(\mathrm{O}\) inside with Euclidean center \(\mathrm{C}\), and the point \(\mathrm{P}\) outside of that circle, from which the Poincaré tangents are to be constructed, is in the mess in the middle. The perpendicular to ray \(\mathrm{OP}\) at \(\mathrm{P}\) establishes \(\mathrm{Q}\) and intersection of the tangent at \(\mathrm{Q}\) with ray \(\mathrm{OP}\) establishes \(\mathrm{P}^{*}\), the inversion of \(P\) in \(\gamma\). The circle centered at \(P^{*}\) of radius \(P * Q\) establishes the Poincaré line \(\ell\), the reflection in which \(\mathrm{P}\) is carried to \(\mathrm{O}=\mathrm{P}^{\prime}\). The reflection of the Poincaré plane in this line carries the circle in question to another circle inside the defining circle. One way of establishing that reflected circle is to reflect the diametric points \(\mathrm{X}\) and \(\mathrm{Y}\) established by the ray \(\mathrm{P}{ }^{*} \mathrm{C}\) to establish diametric points of the inverted circle \(X^{\prime}\) and \(Y^{\prime}\). The Euclidean center of this (also Poincaré) circle \(M\) is just the Euclidean midpoint of segment \(X^{\prime} Y^{\prime}\) needed to construct \(\alpha^{\prime}\), the reflection of the circle \(\alpha\) in line \(\ell\) and to construct points \(A\) and \(B\), the Euclidean points of tangency from \(\mathrm{O}\) to \(\alpha^{\prime}\), hence the Euclidean tangents to \(\alpha^{\prime}\) themselves (included here but really not used in the construction). Reflecting \(A\) and \(B\) in the inverting line \(l\) to establish \(\mathrm{A}^{\prime}\) and \(\mathrm{B}^{\prime}\) on the original circle \(\alpha\), we have determined the points of tangency (since inversion in a circle preserves angles including orthogonality that will establish Poincaré tangency). Since A’, P, P* must lie on the Euclidean circle, we can constructed the circle by constructing it center \(\mathrm{C}_{\mathrm{PA}^{\prime}}\) (off the top of the figure) and the arc of the circle is the Poincaré tangent ray \(\mathrm{PA}^{\prime}\) and similarly \(\mathrm{C}_{\mathrm{PB}^{\prime}}\) (shown) and the Poincaré tangents are constructed.