1.7: Dimensionless Variables
- Page ID
- 19312
This section shows how solving systems of equations can be used to determine appropriate dimensionless variables. It is only an introduction to this topic and considers a specific example of a simple airplane wing shown below. We assume for simplicity that it is a flat plane at an angle to the wind which is blowing against it with speed \(V\) as shown.
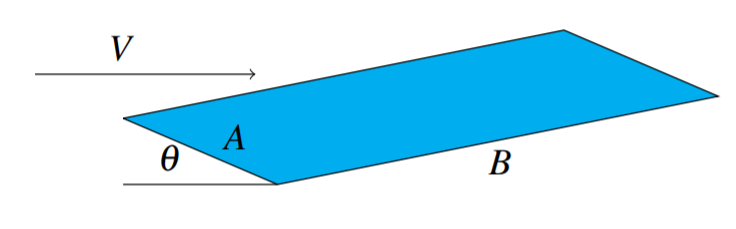
The angle \(\theta\) is called the angle of incidence, \(B\) is the span of the wing and \(A\) is called the chord. Denote by \(l\) the lift. Then this should depend on various quantities like \(\theta ,V,B,A\) and so forth. Here is a table which indicates various quantities on which it is reasonable to expect \(l\) to depend.
| Variable | Symbol | Units |
|---|---|---|
| chord | \(A\) | \(m\) |
| span | \(B\) | \(m\) |
| angle incidence | \(\theta\) | \(m^0kg^0sec^0\) |
| speed of wind | \(V\) | \(m sec^{-1}\) |
| speed of sound | \(V_0\) | \(m sec^{-1}\) |
| density of air | \(\rho\) | \(kgm^{-3}\) |
| viscosity | \(\mu\) | \(kg sec^{-1}m^{-1}\) |
| lift | \(l\) | \(kg sec^{-2}m\) |
Here \(m\) denotes meters, \(\sec\) refers to seconds and \(kg\) refers to kilograms. All of these are likely familiar except for \(\mu\), which we will discuss in further detail now.
Viscosity is a measure of how much internal friction is experienced when the fluid moves. It is roughly a measure of how “sticky" the fluid is. Consider a piece of area parallel to the direction of motion of the fluid. To say that the viscosity is large is to say that the tangential force applied to this area must be large in order to achieve a given change in speed of the fluid in a direction normal to the tangential force. Thus \[\mu \left( \text{area}\right) \left( \text{velocity gradient}\right) =\text{ tangential force}\nonumber \] Hence \[\left( \text{units on }\mu \right) m^{2}\left( \frac{m}{\sec m}\right) =kg\sec ^{-2}m\nonumber \] Thus the units on \(\mu\) are \[kg\sec ^{-1}m^{-1}\nonumber \] as claimed above.
Returning to our original discussion, you may think that we would want \[l=f\left( A,B,\theta ,V,V_{0},\rho ,\mu \right)\nonumber \] This is very cumbersome because it depends on seven variables. Also, it is likely that without much care, a change in the units such as going from meters to feet would result in an incorrect value for \(l\). The way to get around this problem is to look for \(l\) as a function of dimensionless variables multiplied by something which has units of force. It is helpful because first of all, you will likely have fewer independent variables and secondly, you could expect the formula to hold independent of the way of specifying length, mass and so forth. One looks for \[l=f\left( g_{1},\cdots ,g_{k}\right) \rho V^{2}AB\nonumber \] where the units on \(\rho V^{2}AB\) are \[\frac{kg}{m^{3}}\left( \frac{m}{\sec }\right) ^{2}m^{2}=\frac{kg\times m}{ \sec ^{2}}\nonumber \] which are the units of force. Each of these \(g_{i}\) is of the form \[A^{x_{1}}B^{x_{2}}\theta ^{x_{3}}V^{x_{4}}V_{0}^{x_{5}}\rho ^{x_{6}}\mu ^{x_{7}} \label{11julye1f}\] and each \(g_{i}\) is independent of the dimensions. That is, this expression must not depend on meters, kilograms, seconds, etc. Thus, placing in the units for each of these quantities, one needs \[m^{x_{1}}m^{x_{2}}\left( m^{x_{4}}\sec ^{-x_{4}}\right) \left( m^{x_{5}}\sec ^{-x_{5}}\right) \left( kgm^{-3}\right) ^{x_{6}}\left( kg\sec ^{-1}m^{-1}\right) ^{x_{7}}=m^{0}kg^{0}\sec ^{0}\nonumber \] Notice that there are no units on \(\theta\) because it is just the radian measure of an angle. Hence its dimensions consist of length divided by length, thus it is dimensionless. Then this leads to the following equations for the \(x_{i}.\)
\[\begin{array}{cc} m: & x_{1}+x_{2}+x_{4}+x_{5}-3x_{6}-x_{7}=0 \\ \sec :\ & -x_{4}-x_{5}-x_{7}=0 \\ kg: & x_{6}+x_{7}=0 \end{array}\nonumber \]
The augmented matrix for this system is
\[\left[ \begin{array}{rrrrrrr|r} 1 & 1 & 0 & 1 & 1 & -3 & -1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \end{array} \right]\nonumber \] The reduced row-echelon form is given by
\[\left[ \begin{array}{rrrrrrr|r} 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \end{array} \right]\nonumber \] and so the solutions are of the form \[\begin{aligned} x_{1} &= -x_{2}-x_{7} \\ x_{3} &= x_{3} \\ x_{4} &= -x_{5}-x_{7} \\ x_{6} &= -x_{7}\end{aligned}\] Thus, in terms of vectors, the solution is \[\left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ x_{5} \\ x_{6} \\ x_{7} \end{array} \right] =\left[ \begin{array}{c} -x_{2}-x_{7} \\ x_{2} \\ x_{3} \\ -x_{5}-x_{7} \\ x_{5} \\ -x_{7} \\ x_{7} \end{array} \right]\nonumber \] Thus the free variables are \(x_{2},x_{3},x_{5},x_{7}.\) By assigning values to these, we can obtain dimensionless variables by placing the values obtained for the \(x_{i}\) in the formula \(\eqref{11julye1f}\). For example, let \(x_{2}=1\) and all the rest of the free variables are 0. This yields \[x_{1}=-1,x_{2}=1,x_{3}=0,x_{4}=0,x_{5}=0,x_{6}=0,x_{7}=0\nonumber \] The dimensionless variable is then \(A^{-1}B^{1}\). This is the ratio between the span and the chord. It is called the aspect ratio, denoted as \(AR\). Next let \(x_{3}=1\) and all others equal zero. This gives for a dimensionless quantity the angle \(\theta\). Next let \(x_{5}=1\) and all others equal zero. This gives \[x_{1}=0,x_{2}=0,x_{3}=0,x_{4}=-1,x_{5}=1,x_{6}=0,x_{7}=0\nonumber \] Then the dimensionless variable is \(V^{-1}V_{0}^{1}.\) However, it is written as \(V/V_{0}\). This is called the Mach number \(\mathcal{M}\). Finally, let \(x_{7}=1\) and all the other free variables equal 0. Then \[x_{1}=-1,x_{2}=0,x_{3}=0,x_{4}=-1,x_{5}=0,x_{6}=-1,x_{7}=1\nonumber \] then the dimensionless variable which results from this is \(A^{-1}V^{-1}\rho ^{-1}\mu .\) It is customary to write it as \(Re=\left( AV\rho \right) /\mu\). This one is called the Reynold’s number. It is the one which involves viscosity. Thus we would look for \[l=f\left(Re,AR,\theta ,\mathcal{M}\right) kg\times m/\sec ^{2}\nonumber \] This is quite interesting because it is easy to vary \(Re\) by simply adjusting the velocity or \(A\) but it is hard to vary things like \(\mu\) or \( \rho\). Note that all the quantities are easy to adjust. Now this could be used, along with wind tunnel experiments to get a formula for the lift which would be reasonable. You could also consider more variables and more complicated situations in the same way.


