5: System of Equations

Last updated
Save as PDF

Page ID: 104116

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

After reading this chapter, you should be able to:

setup simultaneous linear equations in matrix form and vice-versa,
understand the concept of the inverse of a matrix,
know the difference between a consistent and inconsistent system of linear equations, and
learn that a system of linear equations can have a unique solution, no solution or infinite solutions.

Matrix algebra is used for solving systems of equations. Can you illustrate this concept?

Matrix algebra is used to solve a system of simultaneous linear equations. In fact, for many mathematical procedures such as the solution to a set of nonlinear equations, interpolation, integration, and differential equations, the solutions reduce to a set of simultaneous linear equations. Let us illustrate with an example for interpolation.

Example 1

The upward velocity of a rocket is given at three different times on the following table.

Table 5.1. Velocity vs. time data for a rocket
Time, t	Velocity, v
(s )	(m/s)
5	106.8
8	177.2
12	279.2

The velocity data is approximated by a polynomial as

\[v\left( t \right) = at^{2} + {bt} + c,5 \leq t \leq 12 \nonumber \]

Set up the equations in matrix form to find the coefficients $a,b,c$ of the velocity profile.

Solution

The polynomial is going through three data points $\left( t_{1},v_{1} \right),\left( t_{2},v_{2} \right),and\left( t_{3},v_{3} \right)$ where from table 5.1.

\[t_{1} = 5,\ v_{1} = 106.8 \nonumber \]

\[t_{2} = 8,\ v_{2} = 177.2 \nonumber \]

\[t_{3} = 12,\ v_{3} = 279.2 \nonumber \]

Requiring that $v\left( t \right) = at^{2} + {bt} + c$ passes through the three data points gives

\[v\left( t_{1} \right) = v_{1} = at_{1}^{2} + bt_{1} + c \nonumber \]

\[v\left( t_{2} \right) = v_{2} = at_{2}^{2} + bt_{2} + c \nonumber \]

\[v\left( t_{3} \right) = v_{3} = at_{3}^{2} + bt_{3} + c \nonumber \]

Substituting the data $\left( t_{1},v_{1} \right),\left( t_{2},v_{2} \right),\ and\ \left( t_{3},v_{3} \right)$ gives

\[a\left( 5^{2} \right) + b\left( 5 \right) + c = 106.8 \nonumber \]

\[a\left( 8^{2} \right) + b\left( 8 \right) + c = 177.2 \nonumber \]

\[a\left( 12^{2} \right) + b\left( 12 \right) + c = 279.2 \nonumber \]

\[25a + 5b + c = 106.8 \nonumber \]

\[64a + 8b + c = 177.2 \nonumber \]

\[144a + 12b + c = 279.2 \nonumber \]

This set of equations can be rewritten in the matrix form as

\[\begin{bmatrix} 25a + & 5b + & c \\ 64a + & 8b + & c \\ 144a + & 12b + & c \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

The above equation can be written as a linear combination as follows

\[a\begin{bmatrix} 25 \\ 64 \\ 144 \\ \end{bmatrix} + b\begin{bmatrix} 5 \\ 8 \\ 12 \\ \end{bmatrix} + c\begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

and further using matrix multiplication gives

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

The above is an illustration of why matrix algebra is needed. The complete solution to the set of equations is given later in this chapter.

A general set of $m$ linear equations and $n$ unknowns,

\[a_{11}x_{1} + a_{12}x_{2} + \cdots\cdots + a_{1n}x_{n} = c_{1} \nonumber \]

\[a_{21}x_{1} + a_{22}x_{2} + \cdots\cdots + a_{2n}x_{n} = c_{2} \nonumber \]

\[ \text{..........................................} \nonumber \]

\[a_{m1}x_{1} + a_{m2}x_{2} + ........ + a_{mn}x_{n} = c_{m} \nonumber \]

can be rewritten in the matrix form as

\[\begin{bmatrix} a_{11} & a_{12} & . & . & a_{1n} \\ a_{21} & a_{22} & . & . & a_{2n} \\ \vdots & & & & \vdots \\ \vdots & & & & \vdots \\ a_{m1} & a_{m2} & . & . & a_{mn} \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ \cdot \\ \cdot \\ x_{n} \\ \end{bmatrix} = \begin{bmatrix} c_{1} \\ c_{2} \\ \cdot \\ \cdot \\ c_{m} \\ \end{bmatrix} \nonumber \]

Denoting the matrices by $\left\lbrack A \right\rbrack$, $\left\lbrack X \right\rbrack$, and $\left\lbrack C \right\rbrack$, the system of equation is

$\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$, where $\left\lbrack A \right\rbrack$ is called the coefficient matrix, $\left\lbrack C \right\rbrack$ is called the right hand side vector and $\left\lbrack X \right\rbrack$ is called the solution vector.

Sometimes $\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ systems of equations are written in the augmented form. That is

\[\left\lbrack A \ \vdots \ C \right\rbrack = \left\lbrack \begin{matrix} a_{11} & a_{12} & {......} & a_{1n} \\ a_{21} & a_{22} & {......} & a_{2n} \\ \begin{matrix} \vdots \\ \vdots \\ \end{matrix} & \begin{matrix} \\ \\ \end{matrix} & \begin{matrix} \\ \\ \end{matrix} & \begin{matrix} \\ \\ \end{matrix} \\ a_{m1} & a_{m2} & {......} & a_{mn} \\ \end{matrix}\begin{matrix} \vdots \\ \vdots \\ \vdots \\ \vdots \\ \vdots \\ \end{matrix}\begin{matrix} c_{1} \\ c_{2} \\ \\ \\ c_{n} \\ \end{matrix} \right\rbrack \nonumber \]

A system of equations can be consistent or inconsistent. What does that mean?

A system of equations $\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ is consistent if there is a solution, and it is inconsistent if there is no solution. However, a consistent system of equations does not mean a unique solution, that is, a consistent system of equations may have a unique solution or infinite solutions (Figure 1).

Figure $\PageIndex{1}$: Consistent and inconsistent system of equations flow chart.

Example 2

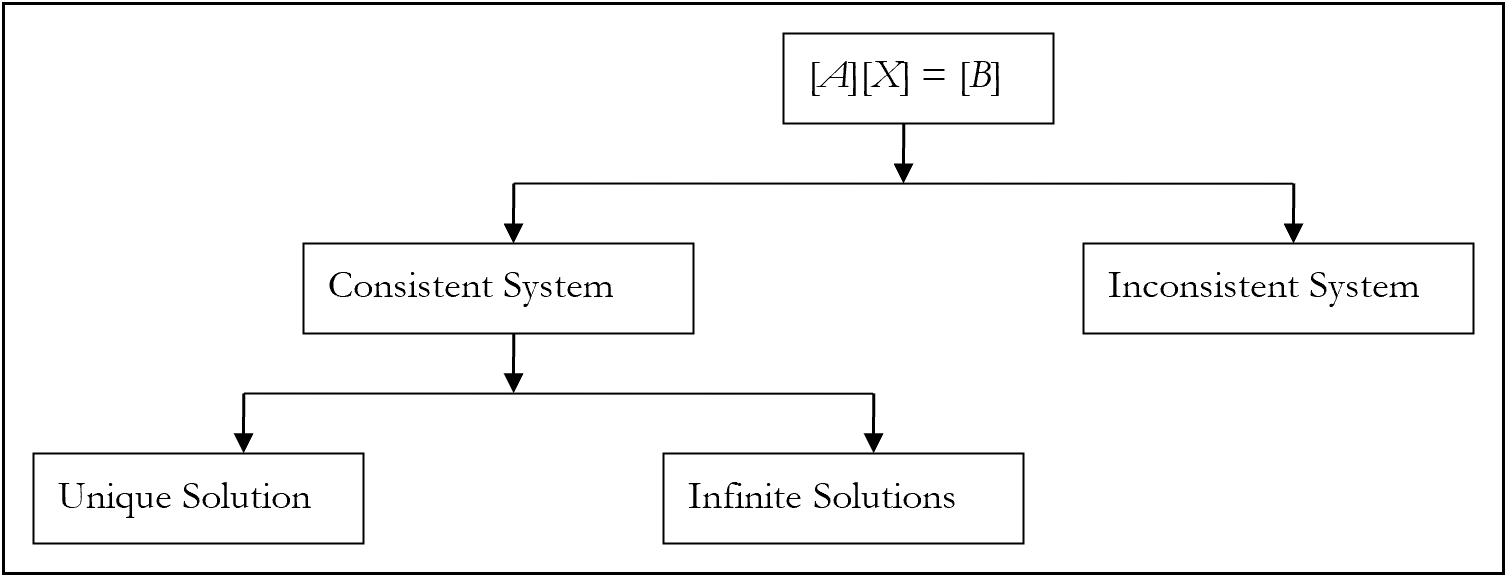
Give examples of consistent and inconsistent system of equations.

Solution

The system of equations

\[\begin{bmatrix} 2 & 4 \\ 1 & 3 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \\ \end{bmatrix} \nonumber \]

is a consistent system of equations as it has a unique solution, that is,

\[\begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ \end{bmatrix} \nonumber \]

The system of equations

\[\begin{bmatrix} 2 & 4 \\ 1 & 2 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 3 \\ \end{bmatrix} \nonumber \]

is also a consistent system of equations but it has infinite solutions as given as follows.

Expanding the above set of equations,

\[2x + 4y = 6 \nonumber \]

\[x + 2y = 3 \nonumber \]

you can see that they are the same equation. Hence, any combination of $\left( x,y \right)$ that satisfies

\[2x + 4y = 6 \nonumber \]

is a solution. For example $\left( x,y \right) = \left( 1,1 \right)$ is a solution. Other solutions include $\left( x,y \right) = (0.5,1.25)$, $\left( x,y \right) = (0,1.5)$, and so on.

The system of equations

\[\begin{bmatrix} 2 & 4 \\ 1 & 2 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \\ \end{bmatrix} \nonumber \]

is inconsistent as no solution exists.

How can one distinguish between a consistent and inconsistent system of equations?

A system of equations $\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ is consistent if the rank of $A$ is equal to the rank of the augmented matrix $\left\lbrack A \ \vdots \ C \right\rbrack$

A system of equations $\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ is inconsistent if the rank of $A$ is less than the rank of the augmented matrix $\left\lbrack A \ \vdots \ C \right\rbrack$.

But, what do you mean by rank of a matrix?

The rank of a matrix is defined as the order of the largest square submatrix whose determinant is not zero.

Example 3

What is the rank of

$\left\lbrack A \right\rbrack = \begin{bmatrix} 3 & 1 & 2 \\ 2 & 0 & 5 \\ 1 & 2 & 3 \\ \end{bmatrix}$?

Solution

The largest square submatrix possible is of order 3 and that is $\lbrack A\rbrack$ itself. Since $det(A) = - 23 \neq 0,$ the rank of $\lbrack A\rbrack = 3.$

Example 4

What is the rank of

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 3 & 1 & 2 \\ 2 & 0 & 5 \\ 5 & 1 & 7 \\ \end{bmatrix}? \nonumber \]

Solution

The largest square submatrix of $\lbrack A\rbrack$ is of order 3 and that is $\lbrack A\rbrack$ itself. Since $det(A) = 0$, the rank of $\lbrack A\rbrack$ is less than 3. The next largest square submatrix would be a $2 \times2$ matrix. One of the square submatrices of $\lbrack A\rbrack$ is

\[\left\lbrack B \right\rbrack = \begin{bmatrix} 3 & 1 \\ 2 & 0 \\ \end{bmatrix} \nonumber \]

and $det(B) = - 2 \neq 0$. Hence the rank of $\lbrack A\rbrack$ is 2. There is no need to look at other $2 \times 2$ submatrices to establish that the rank of $\lbrack A\rbrack$ is 2.

Example 5

How do I now use the concept of rank to find if

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

is a consistent or inconsistent system of equations?

Solution

The coefficient matrix is

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber \]

and the right-hand side vector is

\[\left\lbrack C \right\rbrack = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

The augmented matrix is

\[\left\lbrack B \right\rbrack = \begin{bmatrix} 25 & 5 & 1 & \vdots & 106.8 \\ 64 & 8 & 1 & \vdots & 177.2 \\ 144 & 12 & 1 & \vdots & 279.2 \\ \end{bmatrix} \nonumber \]

Since there are no square submatrices of order 4 as $\lbrack B\rbrack$ is a $3 \times 3$ matrix, the rank of $\lbrack B\rbrack$ is at most $3$. So let us look at the square submatrices of $\lbrack B\rbrack$ of order $3$; if any of these square submatrices have determinant not equal to zero, then the rank is $3$. For example, a submatrix of the augmented matrix $\lbrack B\rbrack$ is

\[\lbrack D\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber \]

has$det(D) = - 84 \neq 0$.

Hence the rank of the augmented matrix $\lbrack B\rbrack$ is 3. Since $\lbrack A\rbrack = \lbrack D\rbrack$, the rank of $\lbrack A\rbrack$ is 3. Since the rank of the augmented matrix $\lbrack B\rbrack$ equals the rank of the coefficient matrix $\lbrack A\rbrack$, the system of equations is consistent.

Example 6

Use the concept of rank of matrix to find if

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 284.0 \\ \end{bmatrix} \nonumber \]

is consistent or inconsistent?

Solution

The coefficient matrix is given by

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix} \nonumber \]

and the right-hand side

\[\left\lbrack C \right\rbrack = \begin{bmatrix} 106.8 \\ 177.2 \\ 284.0 \\ \end{bmatrix} \nonumber \]

The augmented matrix is

\[\left\lbrack B \right\rbrack = \begin{bmatrix} 25 & 5 & 1 & :106.8 \\ 64 & 8 & 1 & :177.2 \\ 89 & 13 & 2 & :284.0 \\ \end{bmatrix} \nonumber \]

Since there are no square submatrices of order 4 as $\lbrack B\rbrack$ is a $4 \times 3$ matrix, the rank of the augmented $\lbrack B\rbrack$ is at most 3. So let us look at square submatrices of the augmented matrix $\lbrack B\rbrack$ of order $3$ and see if any of these have determinants not equal to zero. For example, a square submatrix of the augmented matrix $\lbrack B\rbrack$ is

\[\left\lbrack D \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix} \nonumber \]

has $det(D) = 0$. This means, we need to explore other square submatrices of order 3 of the augmented matrix $\lbrack B\rbrack$ and find their determinants.

That is,

\[\left\lbrack E \right\rbrack = \begin{bmatrix} 5 & 1 & 106.8 \\ 8 & 1 & 177.2 \\ 13 & 2 & 284.0 \\ \end{bmatrix} \nonumber \]

\[det(E) = 0 \nonumber \]

\[\left\lbrack F \right\rbrack = \begin{bmatrix} 25 & 5 & 106.8 \\ 64 & 8 & 177.2 \\ 89 & 13 & 284.0 \\ \end{bmatrix} \nonumber \]

\[det(F) = 0 \nonumber \]

\[\left\lbrack G \right\rbrack = \begin{bmatrix} 25 & 1 & 106.8 \\ 64 & 1 & 177.2 \\ 89 & 2 & 284.0 \\ \end{bmatrix} \nonumber \]

\[det(G) = 0 \nonumber \]

All the square submatrices of order $3 \times 3$ of the augmented matrix $\lbrack B\rbrack$ have a zero determinant. So the rank of the augmented matrix $\lbrack B\rbrack$ is less than 3. Is the rank of augmented matrix $\lbrack B\rbrack$ equal to 2?. One of the $2 \times 2$ submatrices of the augmented matrix $\lbrack B\rbrack$ is

\[\left\lbrack H \right\rbrack = \begin{bmatrix} 25 & 5 \\ 64 & 8 \\ \end{bmatrix} \nonumber \]

and

\[det(H) = - 120 \neq 0 \nonumber \]

So, the rank of the augmented matrix $\lbrack B\rbrack$ is 2.

Now we need to find the rank of the coefficient matrix $\lbrack B\rbrack$.

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix} \nonumber \]

and

\[det(A) = 0 \nonumber \]

So, the rank of the coefficient matrix $\lbrack A\rbrack$ is less than 3. A square submatrix of the coefficient matrix $\lbrack A\rbrack$ is

\[\left\lbrack J \right\rbrack = \begin{bmatrix} 5 & 1 \\ 8 & 1 \\ \end{bmatrix} \nonumber \]

\[det(J) = - 3 \neq 0 \nonumber \]

So, the rank of the coefficient matrix $\lbrack A\rbrack$ is 2.

Hence, rank of the coefficient matrix $\lbrack A\rbrack$ equals the rank of the augmented matrix $[B]$. So the system of equations $\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ is consistent.

Example 7

Use the concept of rank to find if

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 280.0 \\ \end{bmatrix} \nonumber \]

is consistent or inconsistent.

Solution

The augmented matrix is

\[\left\lbrack B \right\rbrack = \begin{bmatrix} 25 & 5 & 1 & :106.8 \\ 64 & 8 & 1 & :177.2 \\ 89 & 13 & 2 & :280.0 \\ \end{bmatrix} \nonumber \]

Since there are no square submatrices of order $4 \times 4$ as the augmented matrix $\lbrack B\rbrack$ is a $4 \times 3$ matrix, the rank of the augmented matrix $\lbrack B\rbrack$ is at most 3. So let us look at square submatrices of the augmented matrix $(B)$ of order 3 and see if any of the $3 \times 3$ submatrices have a determinant not equal to zero. For example, a square submatrix of order $3 \times 3$ of $\lbrack B\rbrack$

\[\left\lbrack D \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix} \nonumber \]

\[\det(D)\ = \ 0 \nonumber \]

So, it means, we need to explore other square submatrices of the augmented matrix $\lbrack B\rbrack$

\[\left\lbrack E \right\rbrack = \begin{bmatrix} 5 & 1 & 106.8 \\ 8 & 1 & 177.2 \\ 13 & 2 & 280.0 \\ \end{bmatrix} \nonumber \]

$det(E) = 12.0 \neq 0$.

So, the rank of the augmented matrix $\lbrack B\rbrack$ is 3.

The rank of the coefficient matrix $\lbrack A\rbrack$ is 2 from the previous example.

Since the rank of the coefficient matrix $\lbrack A\rbrack$ is less than the rank of the augmented matrix $\lbrack B\rbrack$, the system of equations is inconsistent. Hence, no solution exists for $\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$.

If a solution exists, how do we know whether it is unique?

In a system of equations $\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ that is consistent, the rank of the coefficient matrix $\lbrack A\rbrack$ is the same as the augmented matrix $\lbrack A\left| C \right.\ \rbrack$. If in addition, the rank of the coefficient matrix $\lbrack A\rbrack$ is same as the number of unknowns, then the solution is unique; if the rank of the coefficient matrix $\lbrack A\rbrack$ is less than the number of unknowns, then infinite solutions exist.

Figure $\PageIndex{2}$: Flow chart of conditions for consistent and inconsistent system of equations.

Example 8

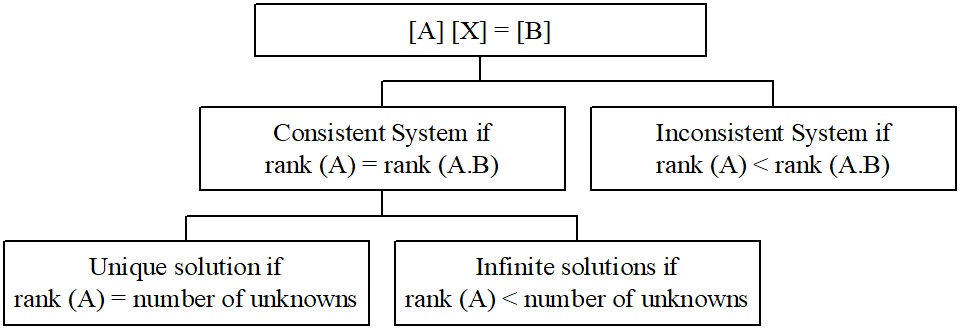
We found that the following system of equations

is a consistent system of equations. Does the system of equations have a unique solution or does it have infinite solutions?

Solution

The coefficient matrix is

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber \]

and the right-hand side is

\[\left\lbrack C \right\rbrack = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

While finding out whether the above equations were consistent in an earlier example, we found that the rank of the coefficient matrix (A) equals rank of augmented matrix $\left\lbrack A \ \vdots \ C \right\rbrack$ equals 3.

The solution is unique as the number of unknowns = 3 = rank of (A).

Example 9

We found that the following system of equations

is a consistent system of equations. Is the solution unique or does it have infinite solutions.

Solution

While finding out whether the above equations were consistent, we found that the rank of the coefficient matrix $\lbrack A\rbrack$equals the rank of augmented matrix $\left( A \ \vdots\ C \right)$ equals 2

Since the rank of $\lbrack A\rbrack = 2$ < number of unknowns = 3, infinite solutions exist.

If we have more equations than unknowns in [A] [X] = [C], does it mean the system is inconsistent?

No, it depends on the rank of the augmented matrix $\left\lbrack A\ \vdots \ C \right\rbrack$ and the rank of $\lbrack A\rbrack$.

For example

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ 284.0 \\ \end{bmatrix} \nonumber \]

is consistent, since

rank of augmented matrix = 3
rank of coefficient matrix = 3

Now since the rank of (A) = 3 = number of unknowns, the solution is not only consistent but also unique.

For example

is inconsistent, since

rank of augmented matrix = $4$
rank of coefficient matrix = $3$

For example

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 50 & 10 & 2 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 213.6 \\ 280.0 \\ \end{bmatrix} \nonumber \]

is consistent, since

rank of augmented matrix = 2
rank of coefficient matrix = 2

But since the rank of $\lbrack A\rbrack$ = 2 < the number of unknowns = 3, infinite solutions exist.

Consistent systems of equations can only have a unique solution or infinite solutions. Can a system of equations have more than one but not infinite number of solutions?

No, you can only have either a unique solution or infinite solutions. Let us suppose $\lbrack A\rbrack\lbrack X\rbrack = \lbrack C\rbrack$has two solutions $\lbrack Y\rbrack$ and $\lbrack Z\rbrack$ so that

\[\lbrack A\rbrack\lbrack Y\rbrack = \lbrack C\rbrack \nonumber \]

\[\lbrack A\rbrack\lbrack Z\rbrack = \lbrack C\rbrack \nonumber \]

If $r$ is a constant, then from the two equations

\[r\left\lbrack A \right\rbrack\left\lbrack Y \right\rbrack = r\left\lbrack C \right\rbrack \nonumber \]

\[\left( 1 - r \right)\left\lbrack A \right\rbrack\left\lbrack Z \right\rbrack = \left( 1 - r \right)\left\lbrack C \right\rbrack \nonumber \]

Adding the above two equations gives

\[r\left\lbrack A \right\rbrack\left\lbrack Y \right\rbrack + \left( 1 - r \right)\left\lbrack A \right\rbrack\left\lbrack Z \right\rbrack = r\left\lbrack C \right\rbrack + \left( 1 - r \right)\left\lbrack C \right\rbrack \nonumber \]

\[\left\lbrack A \right\rbrack\left( r\left\lbrack Y \right\rbrack + \left( 1 - r \right)\left\lbrack Z \right\rbrack \right) = \left\lbrack C \right\rbrack \nonumber \]

Hence

\[r\left\lbrack Y \right\rbrack + \left( 1 - r \right)\left\lbrack Z \right\rbrack \nonumber \]

is a solution to

\[\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack \nonumber \]

Since $r$ is any scalar, there are infinite solutions for $\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ of the form

\[r\left\lbrack Y \right\rbrack + \left( 1 - r \right)\left\lbrack Z \right\rbrack \nonumber \]

Can you divide two matrices?

If $\lbrack A\rbrack\ \lbrack B\rbrack = \lbrack C\rbrack$ is defined, it might seem intuitive that $\lbrack A\rbrack = \frac{\left\lbrack C \right\rbrack}{\left\lbrack B \right\rbrack}$, but matrix division is not defined like that. However an inverse of a matrix can be defined for certain types of square matrices. The inverse of a square matrix $\lbrack A\rbrack$, if existing, is denoted by $\lbrack A\rbrack^{- 1}$ such that

\[\lbrack A\rbrack\ \lbrack A\rbrack^{- 1} = \lbrack I\rbrack = \lbrack A\rbrack^{- 1}\lbrack A\rbrack \nonumber \]

Where $\lbrack I\rbrack$ is the identity matrix.

In other words, let $[A]$ be a square matrix. If $\lbrack B\rbrack$ is another square matrix of the same size such that $\lbrack B\rbrack\ \lbrack A\rbrack = \lbrack I\rbrack$, then $\lbrack B\rbrack$ is the inverse of $\lbrack A\rbrack$. $\lbrack A\rbrack$ is then called to be invertible or nonsingular. If $\lbrack A\rbrack^{- 1}$ does not exist, $\lbrack A\rbrack$ is called noninvertible or singular.

If $\lbrack A\rbrack$ and $\lbrack B\rbrack$ are two $n \times n$ matrices such that $\lbrack B\rbrack\ \lbrack A\rbrack = \lbrack I\rbrack$, then these statements are also true

$[B]$ is the inverse of $[A]$

$[A]$ is the inverse of $[B]$

$[A]$ and $[B]$ are both invertible

$[A]$ $[B]$=$[I]$.

$[A]$ and $[B]$ are both nonsingular

all columns of $[A]$ and $[B]$ are linearly independent

all rows of $[A]$ and $[B]$ are linearly independent.

Example 10

Determine if

\[\lbrack B\rbrack = \begin{bmatrix} 3 & 2 \\ 5 & 3 \\ \end{bmatrix}\ \nonumber \]

is the inverse of

\[\lbrack A\rbrack = \begin{bmatrix} - 3 & 2 \\ 5 & - 3 \\ \end{bmatrix} \nonumber \]

Solution

\[\begin{split} \lbrack B\rbrack\lbrack A\rbrack &= \ \ \begin{bmatrix} 3 & 2 \\ 5 & 3 \\ \end{bmatrix}\begin{bmatrix} - 3 & 2 \\ 5 & - 3 \\ \end{bmatrix}\\ &= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\\ &= \lbrack I\rbrack \end{split} \nonumber \]

Since

\[\ \left\lbrack B \right\rbrack\left\lbrack A \right\rbrack = \left\lbrack I \right\rbrack, \nonumber \]

$\lbrack B\rbrack$ is the inverse of $[A]$ and $\lbrack A\rbrack$ is the inverse of $\lbrack B\rbrack$.

But, we can also show that

\[\begin{split} \lbrack A\rbrack\lbrack B\rbrack &= \begin{bmatrix} - 3 & 2 \\ 5 & - 3 \\ \end{bmatrix}\begin{bmatrix} 3 & 2 \\ 5 & 3 \\ \end{bmatrix}\\ &= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\\ &= \lbrack I\rbrack \end{split} \nonumber \]

to show that $\lbrack A\rbrack$ is the inverse of $\lbrack B\rbrack$.

Can I use the concept of the inverse of a matrix to find the solution of a set of equations [A] [X] = [C]?

Yes, if the number of equations is the same as the number of unknowns, the coefficient matrix $\lbrack A\rbrack$ is a square matrix.

Given

\[\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack \nonumber \]

Then, if $\lbrack A\rbrack^{- 1}$ exists, multiplying both sides by $\lbrack A\rbrack^{- 1}$.

\[\lbrack A\rbrack^{- 1}\lbrack A\rbrack\lbrack X\rbrack = \lbrack A\rbrack^{- 1}\lbrack C\rbrack \nonumber \]

\[\lbrack I\rbrack\ \lbrack X\rbrack = \lbrack A\rbrack^{- 1}\lbrack C\rbrack \nonumber \]

\[\lbrack X\rbrack = \lbrack A\rbrack^{- 1}\lbrack C\rbrack \nonumber \]

This implies that if we are able to find $\lbrack A\rbrack^{- 1}$, the solution vector of $\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ is simply a multiplication of $\lbrack A\rbrack^{- 1}$ and the right hand side vector, $\lbrack C\rbrack$.

How do I find the inverse of a matrix?

If $\lbrack A\rbrack$ is a $n \times n$ matrix, then $\lbrack A\rbrack^{- 1}$ is a $n \times n$ matrix and according to the definition of inverse of a matrix

\[\lbrack A\rbrack\ \lbrack A\rbrack^{- 1} = \lbrack I\rbrack \nonumber \]

Denoting

\[\lbrack A\rbrack = \begin{bmatrix} a_{11} & a_{12} & \cdot & \cdot & a_{1n} \\ a_{21} & a_{22} & \cdot & \cdot & a_{2n} \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ a_{n1} & a_{n2} & \cdot & \cdot & a_{nn} \\ \end{bmatrix} \nonumber \]

\[\lbrack A\rbrack^{- 1} = \begin{bmatrix} a_{11}^{'} & a_{12}^{'} & \cdot & \cdot & a_{1n}^{'} \\ a_{21}^{'} & a_{22}^{'} & \cdot & \cdot & a_{2n}^{'} \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ a_{n1}^{'} & a_{n2}^{'} & \cdot & \cdot & a_{nn}^{'} \\ \end{bmatrix} \nonumber \]

\[\lbrack I\rbrack = \begin{bmatrix} 1 & 0 & \cdot & \cdot & \cdot & 0 \\ 0 & 1 & & & & 0 \\ 0 & & \cdot & & & \cdot \\ \cdot & & & 1 & & \cdot \\ \cdot & & & & \cdot & \cdot \\ 0 & \cdot & \cdot & \cdot & \cdot & 1 \\ \end{bmatrix} \nonumber \]

Using the definition of matrix multiplication, the first column of the $\lbrack A\rbrack^{- 1}$ matrix can then be found by solving

\[\begin{bmatrix} a_{11} & a_{12} & \cdot & \cdot & a_{1n} \\ a_{21} & a_{22} & \cdot & \cdot & a_{2n} \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ a_{n1} & a_{n2} & \cdot & \cdot & a_{nn} \\ \end{bmatrix}\begin{bmatrix} a_{11}^{'} \\ a_{21}^{'} \\ \cdot \\ \cdot \\ a_{n1}^{'} \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ \cdot \\ \cdot \\ 0 \\ \end{bmatrix} \nonumber \]

Similarly, one can find the other columns of the $\lbrack A\rbrack^{- 1}$ matrix by changing the right hand side accordingly.

Example 11

The upward velocity of the rocket is given by

Table 5.2. Velocity vs time data for a rocket
Time, $t$ (s)	Velocity, $v$ (m/s)
5	106.8
8	177.2
12	279.2

In an earlier example, we wanted to approximate the velocity profile by

\[v\left( t \right) = at^{2} + {bt} + c,5 \leq t \leq 12 \nonumber \]

We found that the coefficients $a,\ b,\ and\ c$ in $v\left( t \right)$ are given by

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

First, find the inverse of

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber \]

and then use the definition of inverse to find the coefficients $a,\ b,\ and\ c.$

Solution

\[\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} a_{11}^{'} & a_{12}^{'} & a_{13}^{'} \\ a_{21}^{'} & a_{22}^{'} & a_{23}^{'} \\ a_{31}^{'} & a_{32}^{'} & a_{33}^{'} \\ \end{bmatrix} \nonumber \]

is the inverse of $\lbrack A\rbrack$, then

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{11}^{'} & a_{12}^{'} & a_{13}^{'} \\ a_{21}^{'} & a_{22}^{'} & a_{23}^{'} \\ a_{31}^{'} & a_{32}^{'} & a_{33}^{'} \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \nonumber \]

gives three sets of equations

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{11}^{'} \\ a_{21}^{'} \\ a_{31}^{'} \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix} \nonumber \]

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{12}^{'} \\ a_{22}^{'} \\ a_{32}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix} \nonumber \]

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{13}^{'} \\ a_{23}^{'} \\ a_{33}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ \end{bmatrix} \nonumber \]

Solving the above three sets of equations separately gives

\[\begin{bmatrix} a_{11}^{'} \\ a_{21}^{'} \\ a_{31}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0.04762 \\ - 0.9524 \\ 4.571 \\ \end{bmatrix} \nonumber \]

\[\begin{bmatrix} a_{12}^{'} \\ a_{22}^{'} \\ a_{32}^{'} \\ \end{bmatrix} = \begin{bmatrix} - 0.08333 \\ 1.417 \\ - 5.000 \\ \end{bmatrix} \nonumber \]

\[\begin{bmatrix} a_{13}^{'} \\ a_{23}^{'} \\ a_{33}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0.03571 \\ - 0.4643 \\ 1.429 \\ \end{bmatrix} \nonumber \]

Hence

\[\lbrack A\rbrack^{- 1} = \begin{bmatrix} 0.04762 & - 0.08333 & 0.03571 \\ - 0.9524 & 1.417 & - 0.4643 \\ 4.571 & - 5.000 & 1.429 \\ \end{bmatrix} \nonumber \]

Now

\[\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack \nonumber \]

where

\[\left\lbrack X \right\rbrack = \begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} \nonumber \]

\[\left\lbrack C \right\rbrack = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

Using the definition of $\left\lbrack A \right\rbrack^{- 1},$

\[\left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack \nonumber \]

\[\left\lbrack X \right\rbrack = \left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack \nonumber \]

\[\begin{bmatrix} 0.04762 & - 0.08333 & 0.03571 \\ - 0.9524 & 1.417 & - 0.4643 \\ 4.571 & - 5.000 & 1.429 \\ \end{bmatrix}\begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

Hence

\[\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 0.2905 \\ 19.69 \\ 1.086 \\ \end{bmatrix} \nonumber \]

\[v\left( t \right) = 0.2905t^{2} + 19.69t + 1.086,5 \leq t \leq 12 \nonumber \]

Is there another way to find the inverse of a matrix?

For finding the inverse of small matrices, the inverse of an invertible matrix can be found by

\[\left\lbrack A \right\rbrack^{- 1} = \frac{1}{\det\left( A \right)}{adj}\left( A \right) \nonumber \]

where

\[{adj}\left( A \right) = \begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1n} \\ C_{21} & C_{22} & & C_{2n} \\ \vdots & & & \\ C_{n1} & C_{n2} & \cdots & C_{nn} \\ \end{bmatrix}^{T} \nonumber \]

where $C_{ij}$ are the cofactors of $a_{ij}$. The matrix

\[\begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1n} \\ C_{21} & C_{22} & \cdots & C_{2n} \\ \vdots & & & \vdots \\ C_{n1} & \cdots & \cdots & C_{nn} \\ \end{bmatrix} \nonumber \]

itself is called the matrix of cofactors from $[A]$. Cofactors are defined in Chapter 4.

Example 12

Find the inverse of

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber \]

Solution

From Example 4.6 in Chapter 04.06, we found

\[\det\left( A \right) = - 84 \nonumber \]

Next we need to find the adjoint of $\lbrack A\rbrack$. The cofactors of $A$ are found as follows.

The minor of entry $a_{11}$ is

\[\begin{split} M_{11} &= \left| \begin{matrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{matrix} \right|\\ &= \left| \begin{matrix} 8 & 1 \\ 12 & 1 \\ \end{matrix} \right|\\ &= - 4 \end{split} \nonumber \]

The cofactors of entry $a_{11}$ is

\[\begin{split} C_{11} &= \left( - 1 \right)^{1 + 1}M_{11}\\ &= M_{11}\\ &= - 4 \end{split} \nonumber \]

The minor of entry $a_{12}$ is

\[\begin{split} M_{12} &= \left| \begin{matrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{matrix} \right|\\ &= \left| \begin{matrix} 64 & 1 \\ 144 & 1 \\ \end{matrix} \right|\\ &= - 80 \end{split} \nonumber \]

The cofactor of entry $a_{12}$ is

\[\begin{split} C_{12} &= \left( - 1 \right)^{1 + 2}M_{12}\\ &= - M_{12}\\ &= - ( - 80)\\ &= 80 \end{split} \nonumber \]

Similarly

\[C_{13} = - 384 \nonumber \]

\[C_{21} = 7 \nonumber \]

\[C_{22} = - 119 \nonumber \]

\[C_{23} = 420 \nonumber \]

\[C_{31} = - 3 \nonumber \]

\[C_{32} = 39 \nonumber \]

\[C_{33} = - 120 \nonumber \]

Hence the matrix of cofactors of $\lbrack A\rbrack$ is

\[\left\lbrack C \right\rbrack = \begin{bmatrix} - 4 & 80 & - 384 \\ 7 & - 119 & 420 \\ - 3 & 39 & - 120 \\ \end{bmatrix} \nonumber \]

The adjoint of matrix $\lbrack A\rbrack$ is $\lbrack C\rbrack^{T}$,

\[\begin{split} {adj}\left( A \right) &= \left\lbrack C \right\rbrack^{T}\\ &= \begin{bmatrix} - 4 & 7 & - 3 \\ 80 & - 119 & 39 \\ - 384 & 420 & - 120 \\ \end{bmatrix} \end{split} \nonumber \]

Hence

\[\begin{split} \left\lbrack A \right\rbrack^{- 1} &= \frac{1}{\det\left( A \right)}{adj}\left( A \right)\\ &= \frac{1}{- 84}\begin{bmatrix} - 4 & 7 & - 3 \\ 80 & - 119 & 39 \\ - 384 & 420 & - 120 \\ \end{bmatrix}\\ &= \begin{bmatrix} 0.04762 & - 0.08333 & 0.03571 \\ - 0.9524 & 1.417 & - 0.4643 \\ 4.571 & - 5.000 & 1.429 \\ \end{bmatrix} \end{split} \nonumber \]

If the inverse of a square matrix [A] exists, is it unique?

Yes, the inverse of a square matrix is unique, if it exists. The proof is as follows. Assume that the inverse of $\lbrack A\rbrack$ is $\lbrack B\rbrack$ and if this inverse is not unique, then let another inverse of $\lbrack A\rbrack$ exist called $\lbrack C\rbrack$.

If $\lbrack B\rbrack$ is the inverse of $\lbrack A\rbrack$, then

\[\lbrack B\rbrack\ \lbrack A\rbrack = \lbrack I\rbrack \nonumber \]

Multiply both sides by $\lbrack C\rbrack$,

\[\lbrack B\rbrack\ \lbrack A\rbrack\ \lbrack C\rbrack = \lbrack I\rbrack\ \lbrack C\rbrack \nonumber \]

\[\lbrack B\rbrack\ \lbrack A\rbrack\ \lbrack C\rbrack = \lbrack C\rbrack \nonumber \]

Since $[C]$ is inverse of $\lbrack A\rbrack$,

\[\lbrack A\rbrack\ \lbrack C\rbrack = \lbrack I\rbrack\ \nonumber \]

Multiply both sides by $\lbrack B\rbrack$,

\[\lbrack B\rbrack\ \lbrack I\rbrack\ = \lbrack C\rbrack \nonumber \]

\[\lbrack B\rbrack\ = \lbrack C\rbrack \nonumber \]

This shows that $\lbrack B\rbrack$ and $\lbrack C\rbrack$ are the same. So the inverse of $\lbrack A\rbrack$ is unique.

System of Equations Quiz

Quiz 1

A $3 \times 4$ matrix can have a rank of at most

(A) $3$

(B) $4$

(D) $12$

Quiz 2

Three kids – Jim, Corey and David receive an inheritance of $\text{\$} 2,253,453$. The money is put in three trusts but is not divided equally to begin with. Corey gets three times what David gets because Corey made an “A” in Dr. Kaw’s class. Each trust is put in an interest generating investment. The three trusts of Jim, Corey and David pay an interest of $6\%$, $8\%$, $11\%$, respectively. The total interest of all the three trusts combined at the end of the first year is $\text{\$}190,740.57$. How much money was invested in each trust? The equations in a matrix form are

(A) $\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 3 \\ .06 & .08 & .11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2253543 \\ 0 \\ 190740.57 \\ \end{bmatrix}$

(B) $\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & - 3 \\ .06 & .08 & .11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2253543 \\ 0 \\ 190740.57 \\ \end{bmatrix}$

(C) $\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & - 3 \\ 6 & 8 & 11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2253543 \\ 0 \\ 190740.57 \\ \end{bmatrix}$

(D) $\begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & - 3 \\ .06 & .08 & .11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2253543 \\ 0 \\ 190740.57 \\ \end{bmatrix}$

Quiz 3

Which of the following matrices does not have an inverse?

(A) $\begin{bmatrix} 5 & 6 \\ 7 & 8 \\ \end{bmatrix}$

(B) $\begin{bmatrix} 6 & 7 \\ 12 & 14 \\ \end{bmatrix}$

(D) $\begin{bmatrix} 0 & 6 \\ 7 & 0 \\ \end{bmatrix}$

Quiz 4

The set of equations

\[\begin{bmatrix} 1 & 2 & 5 \\ 2 & 3 & 7 \\ 5 & 8 & 19 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 18 \\ 26 \\ 70 \\ \end{bmatrix} \nonumber \]

has

(A) no solution

(B) finite number of solutions

(D) infinite solutions

Quiz 5

Given a system of $\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$where $\left\lbrack A \right\rbrack$is $n \times n$ matrix and $\left\lbrack X \right\rbrack$and $\left\lbrack C \right\rbrack$are $n \times 1$ matrices, a unique solution $\left\lbrack X \right\rbrack$exists if

(A) rank of $\left\lbrack A \right\rbrack =$ rank of $\left\lbrack A \vdots C \right\rbrack$

(B) rank of $\left\lbrack A \right\rbrack =$ rank of $\left\lbrack A \vdots C \right\rbrack = n$

(D) rank of $\left\lbrack A \right\rbrack =$ rank of $\left\lbrack A \vdots C \right\rbrack < n$

Quiz 6

If $\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \begin{bmatrix} - 13 \\ 76 \\ 38 \\ \end{bmatrix}$ and $\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} 1 & 2 & - 4 \\ - 8 & 2 & 16 \\ 2 & 4 & 8 \\ \end{bmatrix}$ then

(A) $\left\lbrack X \right\rbrack = \begin{bmatrix} -13.000 \\ 864.00 \\ 582.00 \\ \end{bmatrix}$

(B) one cannot find a unique $\left\lbrack X \right\rbrack$.

(D) no solutions of $\left\lbrack X \right\rbrack$ are possible

System of Equations Exercise

Exercise 1

For a set of equations $\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack B\rbrack$, a unique solution exists if

rank (A) = rank $\left( A\ \vdots\ B \right)$
rank (A) = rank $\left( A\ \vdots\ B \right)$ and rank (A) = number of unknowns
rank (A) = rank $\left( A\ \vdots\ B \right)$ and rank (A) = number of rows of (A).

Answer: B

Exercise 2

The rank of matrix

$A = \begin{bmatrix} 4 & 4 & 4 & 4 \\ 4 & 4 & 4 & 4 \\ 4 & 4 & 4 & 4 \\ 4 & 4 & 4 & 4 \\ \end{bmatrix}$ is

$1$
$2$
$3$
$4$

Exercise 3

A $3 \times 4$ matrix can have a rank of at most

$3$
$4$
$5$
$12$

Exercise 4

If $\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ has a unique solution, where the order of $\lbrack A\rbrack$ is $3 \times 3$, $\lbrack X\rbrack$ is $3 \times 1$, then the rank of $\lbrack A\rbrack$ is

$2$
$3$
$4$
$5$

Exercise 5

Show if the following system of equations is consistent or inconsistent. If they are consistent, determine if the solution would be unique or infinite ones exist.

$\begin{bmatrix} 1 & 2 & 5 \\ 7 & 3 & 9 \\ 8 & 5 & 14 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 8 \\ 19 \\ 27 \\ \end{bmatrix}$

Answer: Consistent; Infinite solutions

Exercise 6

Show if the following system of equations is consistent or inconsistent. If they are consistent, determine if the solution would be unique or infinite ones exist.

$\begin{bmatrix} 1 & 2 & 5 \\ 7 & 3 & 9 \\ 8 & 5 & 14 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 8 \\ 19 \\ 28 \\ \end{bmatrix}$

Answer: Inconsistent

Exercise 7

Show if the following system of equations is consistent or inconsistent. If they are consistent, determine if the solution would be unique or infinite ones exist.

$\begin{bmatrix} 1 & 2 & 5 \\ 7 & 3 & 9 \\ 8 & 5 & 13 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 8 \\ 19 \\ 28 \\ \end{bmatrix}$

Answer: Consistent; Unique

Exercise 8

The set of equations

$\begin{bmatrix} 1 & 2 & 5 \\ 7 & 3 & 9 \\ 8 & 5 & 14 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 8 \\ 19 \\ 27 \\ \end{bmatrix}$

has

Unique solution
No solution
Infinite solutions

Answer: C

Exercise 9

For what values of $a$ will the following equation have

$x_{1} + x_{2} + x_{3} = 4$

$x_{3} = 2$

$\left( a^{2} - 4 \right)x_{1} + x_{3} = a - 2$

Unique solution
No solution
Infinite solutions

Answer: If $a \neq + 2 \ \text{or} -2,$ then there will be a unique solution If $a = + 2 \ or - 2,$ then there will be no solution.
Possibility of infinite solutions does not exist.

Exercise 10

Find if

\[\lbrack A\rbrack = \begin{bmatrix} 5 & - 2.5 \\ - 2 & 3 \\ \end{bmatrix} \nonumber \]

and

\[\lbrack B\rbrack = \begin{bmatrix} 0.3 & 0.25 \\ 0.2 & 0.5 \\ \end{bmatrix} \nonumber \]

are inverse of each other.

Answer: Yes

Exercise 11

Find if

\[\lbrack A\rbrack = \begin{bmatrix} 5 & 2.5 \\ 2 & 3 \\ \end{bmatrix} \nonumber \]

and

\[lbrack B\rbrack = \begin{bmatrix} 0.3 & - 0.25 \\ 0.2 & 0.5 \\ \end{bmatrix} \nonumber \]

are inverse of each other.

Answer: No

Exercise 12

Find the

cofactor matrix
adjoint matrix

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 3 & 4 & 1 \\ 2 & - 7 & - 1 \\ 8 & 1 & 5 \\ \end{bmatrix} \nonumber \]

Answer: $\begin{bmatrix} - 34 & - 18 & 58 \\ - 19 & 7 & 29 \\ 3 & 5 & - 29 \\ \end{bmatrix}\begin{bmatrix} - 34 & - 19 & 3 \\ - 18 & 7 & 5 \\ 58 & 29 & - 29 \\ \end{bmatrix}$

Exercise 13

Find $\lbrack A\rbrack^{- 1}$ using any method for
$\lbrack A\rbrack = \begin{bmatrix} 3 & 4 & 1 \\ 2 & - 7 & - 1 \\ 8 & 1 & 5 \\ \end{bmatrix}$

Answer: $\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} 2.931 \times 10^{- 1} & 1.638 \times 10^{- 1} & - 2.586 \times 10^{- 2} \\ 1.552 \times 10^{- 1} & - 6.034 \times 10^{- 2} & - 4.310 \times 10^{- 2} \\ - 5.000 \times 10^{- 1} & - 2.500 \times 10^{- 1} & 2.500 \times 10^{- 1} \\ \end{bmatrix}$

Exercise 14

Prove that if $\lbrack A\rbrack$ and $\lbrack B\rbrack$ are both invertible and are square matrices of same order, then

\[(\lbrack A\rbrack\lbrack B\rbrack)^{- 1} = \lbrack B\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1} \nonumber \]

Answer

\[\left( \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \right)^{- 1} = \left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1} \nonumber \]

Let \[\left\lbrack C \right\rbrack = \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \nonumber \]

\[\begin{split} \left\lbrack C \right\rbrack\left\lbrack B \right\rbrack^{- 1} &= \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\\ &= \left\lbrack A \right\rbrack\left\lbrack I \right\rbrack\\ &= \left\lbrack A \right\rbrack \end{split} \nonumber \]

Again

$\left\lbrack C \right\rbrack = \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack$

\[\begin{split} \left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack &= \left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\\ &= \left\lbrack I \right\rbrack\left\lbrack B \right\rbrack\\ &= \left\lbrack B \right\rbrack \end{split} \nonumber \]

\[\left\lbrack C \right\rbrack\left\lbrack B \right\rbrack^{- 1} = \left\lbrack A \right\rbrack ;\;\;\;\;\;\;\ (1) \nonumber \]

\[\left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack = \left\lbrack B \right\rbrack;\;\;\;\;\;\;\ (2) \nonumber \]

From (1) and (2)

\[\left\lbrack C \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack = \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \nonumber \]

\[\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \nonumber \]

\[\left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \nonumber \]

\[\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack B \right\rbrack \nonumber \]

\[\left\lbrack B^{- 1} \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack B \right\rbrack^{- 1}\left\lbrack B \right\rbrack \nonumber \] \[\left\lbrack B \right\rbrack^{- 1}\left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack I \right\rbrack. \nonumber \]

Exercise 15

What is the inverse of a square diagonal matrix? Does it always exist?

Answer: Hint: Inverse of a square n$\times$n diagonal matrix $\left\lbrack A \right\rbrack$ is $\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} \frac{1}{a_{11}} & 0 & \cdots & 0 \\ 0 & \frac{1}{a_{22}} & \cdots & 0 \\ 0 & & & \vdots \\ \vdots & \cdots & \cdots & \frac{1}{a_{nn}} \\ \end{bmatrix}$
So inverse exists only if $a_{ii} \neq 0$ for all $i$.

Exercise 16

$\lbrack A\rbrack$ and $\lbrack B\rbrack$ are square matrices. If $\lbrack A\rbrack\ \lbrack B\rbrack = \lbrack 0\rbrack$ and $\lbrack A\rbrack$ is invertible, show$\lbrack B\rbrack = 0$.

Answer: \[\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack 0 \right\rbrack \nonumber \] \[\left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack A \right\rbrack^{- 1}\left\lbrack 0 \right\rbrack \nonumber \]

Exercise 17

If $\lbrack A\rbrack\ \lbrack B\rbrack\ \lbrack C\rbrack = \lbrack I\rbrack$, where $\lbrack A\rbrack$, $\lbrack B\rbrack$ and $\lbrack C\rbrack$ are of the same size, show that $\lbrack B\rbrack$ is invertible.

Answer: Hint: $det({AB}) = det(A)det(B)$

Exercise 18

Prove if $\lbrack B\rbrack$ is invertible, $\lbrack A\rbrack\ \lbrack B\rbrack^{- 1} = \lbrack B\rbrack^{- 1}\lbrack A\rbrack$ if and only if $\lbrack A\rbrack\ \lbrack B\rbrack = \lbrack B\rbrack\lbrack A\rbrack$

Answer: Hint: Multiply by $\left\lbrack B \right\rbrack^{- 1}$ on both sides, $\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1} = \left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack^{- 1}$

Exercise 19

For
$\left\lbrack A \right\rbrack = \begin{bmatrix} 10 & - 7 & 0 \\ - 3 & 2.099 & 6 \\ 5 & - 1 & 5 \\ \end{bmatrix}$
$\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} - 0.1099 & - 0.2333 & 0.2799 \\ - 0.2999 & - 0.3332 & 0.3999 \\ 0.04995 & 0.1666 & 6.664 \times 10^{- 5} \\ \end{bmatrix}$
Show

\[{det }\left( A \right) = \frac{1}{{det}\left( A^{- 1} \right)}. \nonumber \]

Exercise 20

For what values of $a$ does the linear system have

\[\begin{matrix} x + y = 2 \\ 6x + 6y = a \\ \end{matrix} \nonumber \]

infinite solutions
unique solution

Answer

A. $12$

B. not possible

Exercise 21

Three kids - Jim, Corey and David receive an inheritance of $\$2,\$253,\$453$. The money is put in three trusts but is not divided equally to begin with. Corey gets three times more than David because Corey made an “A” in Dr. Kaw’s class. Each trust is put in an interest generating investment. The three trusts of Jim, Corey and David pays an interest of $6\%, 8\%, 11\%,$ respectively. The total interest of all the three trusts combined at the end of the first year is $\$190,\$740.57$. How much money was invested in each trust? Set the following as equations in a matrix form. Identify the unknowns. Do not solve for the unknowns.

Answer

$J + C + D = \$2,\$253,\$453$

\[C = 3D \nonumber \]

\[0.06J+0.08C+0.11D = \$190,740.57 \nonumber \] In matrix form

\[\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & - 3 \\ 0.06 & 0.08 & 0.11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2,253,453 \\ 0 \\ 190,740.57 \\ \end{bmatrix} \nonumber \]

Exercise 22

What is the rank of

\[\begin{bmatrix} 1 & 2 & 3 \\ 4 & 6 & 7 \\ 6 & 10 & 13 \\ \end{bmatrix}? \nonumber \]

Justify your answer.

Answer: In the above matrix, 2(Row 1) + Row 2 = Row 3. Hence, rank is less than 3. Row 1 and Row 2 are linearly independent. Hence, the rank of the matrix is 2.

Exercise 23

What is the rank of

\[\begin{bmatrix} 1 & 2 & 3 & 6 \\ 4 & 6 & 7 & 17 \\ 6 & 10 & 13 & 29 \\ \end{bmatrix}? \nonumber \]

Justify your answer.

Answer

The determinant of all the $3 \times 3$ sub-matrices is zero. Hence, the rank is less than 3. Determinant of

\[\begin{bmatrix} 2 & 3 \\ 6 & 7 \\ \end{bmatrix} = - 4 \neq 0. \nonumber \]

Exercise 24

What is the rank of

\[\begin{bmatrix} 1 & 2 & 3 & 6 \\ 4 & 6 & 7 & 18 \\ 6 & 10 & 13 & 30 \\ \end{bmatrix}? \nonumber \]

Justify your answer.

Answer

In the above matrix, 2(Row 1) + Row 2 = Row 3. Hence, rank is less than 3 as the 3 rows are linearly dependant. Determinant of

\[\begin{bmatrix} 2 & 3 \\ 6 & 7 \\ \end{bmatrix} = - 4 \neq 0. \nonumber \]

Hence, the rank is $2$.

Exercise 25

How many solutions does the following system of equations have

\[\begin{bmatrix} 1 & 2 & 3 \\ 4 & 6 & 7 \\ 6 & 10 & 13 \\ \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 17 \\ 29 \\ \end{bmatrix}? \nonumber \]

Justify your answer.

Answer: Rank of $ A = 2$\ Rank of $A|C = 2$\ Number of unknowns = $3.$\ There are infinite solutions since rank of A is less than the number of unknowns.

Exercise 26

How many solutions does the following system of equations have

\[\begin{bmatrix} 1 & 2 & 3 \\ 4 & 6 & 7 \\ 6 & 10 & 13 \\ \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 18 \\ 30 \\ \end{bmatrix}? \nonumber \]

Justify your answer.

Answer: Rank of $A = 2$\ Rank of $A|C = 2$\ Number of unknowns = $3.$\ There are infinite solutions since rank of A is less than the number of unknowns.

Exercise 27

By any scientific method, find the second column of the inverse of

\[\begin{bmatrix} 1 & 2 & 0 \\ 4 & 5 & 0 \\ 0 & 0 & 13 \\ \end{bmatrix}. \nonumber \]

Answer

$\begin{bmatrix} 1 & 2 & 0 \\ 4 & 5 & 0 \\ 0 & 0 & 13 \\ \end{bmatrix}\begin{bmatrix} X & a_{12}^{'} & X \\ X & a_{22}^{'} & X \\ X & a_{32}^{'} & X \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$

\[\begin{matrix} a_{12}^{'} + 2a_{22}^{'} = 0 \\ 4a_{12}^{'} + 5a_{22}^{'} = 1 \\ 13a_{32}^{'} = 0 \\ \end{matrix} \nonumber \]

Simplifying,

\[\begin{bmatrix} a_{12}^{'} \\ a_{22}^{'} \\ a_{32}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0.667 \\ - 0.333 \\ 0 \\ \end{bmatrix} \nonumber \]

Exercise 28

Just write out the inverse of (no need to show any work)

\[\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 4 & 0 \\ 0 & 0 & 0 & 5 \\ \end{bmatrix} \nonumber \]

Answer: $\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \frac{1}{2} & 0 & 0 \\ 0 & 0 & \frac{1}{4} & 0 \\ 0 & 0 & 0 & \frac{1}{5} \\ \end{bmatrix}$

Exercise 29

Solve $\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack B\rbrack$ for $\lbrack X\rbrack\ $ if

\[\lbrack A\rbrack^{- 1} = \begin{bmatrix} 10 & - 7 & 0 \\ 2 & 2 & 5 \\ 2 & 0 & 6 \\ \end{bmatrix} \nonumber \]

and

\[\lbrack B\rbrack = \begin{bmatrix} 7 \\ 2.5 \\ 6.012 \\ \end{bmatrix} \nonumber \]

Answer: \[\begin{split} \lbrack X\rbrack = \lbrack A\rbrack - 1\lbrack B\rbrack\ &= \begin{bmatrix} 10 & - 7 & 0 \\ 2 & 2 & 5 \\ 2 & 0 & 6 \\ \end{bmatrix}\begin{bmatrix} 7 \\ 2.5 \\ 6.012 \\ \end{bmatrix}\\ &=\begin{bmatrix} 52.5 \\ 49.06 \\ 50.072 \\ \end{bmatrix} \end{split} \nonumber \]

Exercise 30

Let $\lbrack A\rbrack\ $ be a $3 \times 3$ matrix. Suppose

\[\lbrack X\rbrack = \begin{bmatrix} 7 \\ 2.5 \\ 6.012 \\ \end{bmatrix} \nonumber \]

is a solution to the homogeneous set of equations $\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack 0\rbrack$ (the right hand side is a zero vector of order $3 \times 1$). Does $\lbrack A\rbrack$ have an inverse? Justify your answer.

Answer

Given

$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack 0\rbrack$
If $\lbrack A\rbrack^{- 1}$exists, then
$\lbrack A\rbrack^{- 1}\ \lbrack A\rbrack\ \lbrack X\rbrack = \lbrack A\rbrack^{- 1}\lbrack 0\rbrack$
$\lbrack I\rbrack\ \lbrack X\rbrack = \lbrack 0\rbrack$
$\lbrack X\rbrack = \lbrack 0\rbrack$
This contradicts the given value of $\lbrack X\rbrack$. Hence, $\lbrack A\rbrack^{- 1}$ does not exist.

Exercise 31

Is the set of vectors

\[\overrightarrow{A} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix},\overrightarrow{B} = \begin{bmatrix} 1 \\ 2 \\ 5 \\ \end{bmatrix},\overrightarrow{C} = \begin{bmatrix} 1 \\ 4 \\ 25 \\ \end{bmatrix} \nonumber \]

linearly independent? Justify your answer.

Answer: The set of vectors are linearly independent.

Exercise 32

What is the rank of the set of vectors

Justify your answer.

Answer: Since, the $3$ vectors are linearly independent as proved above, the rank of the 3 vectors is $3$.

Exercise 33

What is the rank of

\[\overrightarrow{A} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix},\overrightarrow{B} = \begin{bmatrix} 2 \\ 2 \\ 4 \\ \end{bmatrix},\overrightarrow{C} = \begin{bmatrix} 3 \\ 3 \\ 5 \\ \end{bmatrix}? \nonumber \]

Justify your answer.

Answer: By inspection, $\overrightarrow{C} = \overrightarrow{A} + \overrightarrow{B}$. Hence, the 3 vectors are linearly dependent, and the rank is less than 3. Linear combination of$\overrightarrow{A}\text{and}\ \overrightarrow{B}$, that is, $K_{1}\overrightarrow{A} + K_{2}\overrightarrow{B} = 0$has only one solution K₁= K₂ = 0. Therefore, the rank is 2.