10.1: Inner Products and Norms
- Page ID
- 58890
The dot product was introduced in \(\mathbb{R}^n\) to provide a natural generalization of the geometrical notions of length and orthogonality that were so important in Chapter 4 . The plan in this chapter is to define an inner product on an arbitrary real vector space \(V\) (of which the dot product is an example in \(\mathbb{R}^n\) ) and use it to introduce these concepts in \(V\).
An inner product on a real vector space \(V\) is a function that assigns a real number \(\langle\boldsymbol{v}, \boldsymbol{w}\rangle\) to every pair \(\mathbf{v}, \mathbf{w}\) of vectors in \(V\) in such a way that the following axioms are satisfied.
\(P1. \langle\mathbf{v}, \mathbf{w}\rangle\) is a real number for all \(\mathbf{v}\) and \(\mathbf{w}\) in \(V\).
\(P 2 \langle\boldsymbol{v}, \boldsymbol{w}\rangle=\langle\boldsymbol{w}, \boldsymbol{v}\rangle\) for all \(\mathbf{v}\) and \(\mathbf{w}\) in \(V\).
\(P3. \langle\boldsymbol{v}+\boldsymbol{w}, \boldsymbol{u}\rangle=\langle\mathbf{v}, \mathbf{u}\rangle+\langle\mathbf{w}, \mathbf{u}\rangle\) for all \(\mathbf{u}, \mathbf{v}\), and \(\mathbf{w}\) in \(V\).
\(P4. \langle r \mathbf{v}, \mathbf{w}\rangle=r\langle\mathbf{v}, \mathbf{w}\rangle\) for all \(\mathbf{v}\) and \(\mathbf{w}\) in \(V\) and all \(r\) in \(\mathbb{R}\).
\(P5. \langle\mathbf{v}, \mathbf{v}\rangle>0\) for all \(\mathbf{v} \neq \mathbf{0}\) in \(V\).
A real vector space \(V\) with an inner product \(\langle\),\(\rangle\) will be called an inner product space. Note that every subspace of an inner product space is again an inner product space using the same inner product. \(^1\)
\(\mathbb{R}^n\) is an inner product space with the dot product as inner product:
\[
\langle\mathbf{v}, \mathbf{w}\rangle=\mathbf{v} \cdot \mathbf{w} \text { for all } \mathbf{v}, \mathbf{w} \in \mathbb{R}^n
\]
See Theorem 5.3.1. This is also called the euclidean inner product, and \(\mathbb{R}^n\), equipped with the dot product, is called euclidean \(n\)-space.
\({ }^1\) If we regard \(\mathbb{C}^n\) as a vector space over the field \(\mathbb{C}\) of complex numbers, then the "standard inner product" on \(\mathbb{C}^n\) defined in Section 8.6 does not satisfy Axiom P4 (see Theorem 8.6.1(3)).
If \(A\) and \(B\) are \(m \times n\) matrices, define \(\langle A, B\rangle=\operatorname{tr}\left(A B^T\right)\) where \(\operatorname{tr}(X)\) is the trace of the square matrix \(X\). Show that \(\langle\),\(\rangle is an inner product in \mathbf{M}_{m n}\).
Solution
P1 is clear. Since \(\operatorname{tr}(P)=\operatorname{tr}\left(P^T\right)\) for every \(m \times n\) matrix \(P\), we have P2:
\[
\langle A, B\rangle=\operatorname{tr}\left(A B^T\right)=\operatorname{tr}\left[\left(A B^T\right)^T\right]=\operatorname{tr}\left(B A^T\right)=\langle B, A\rangle .
\]
Next, P3 and P4 follow because trace is a linear transformation \(\mathbf{M}_{m n} \rightarrow \mathbb{R}\) (Exercise 19). Turning to P5, let \(\mathbf{r}_1, \mathbf{r}_2, \ldots, \mathbf{r}_m\) denote the rows of the matrix \(A\). Then the \((i, j)\)-entry of \(A A^T\) is \(\mathbf{r}_i \cdot \mathbf{r}_j\), so
\[
\langle A, A\rangle=\operatorname{tr}\left(A A^T\right)=\mathbf{r}_1 \cdot \mathbf{r}_1+\mathbf{r}_2 \cdot \mathbf{r}_2+\cdots+\mathbf{r}_m \cdot \mathbf{r}_m
\]
But \(\mathbf{r}_j \cdot \mathbf{r}_j\) is the sum of the squares of the entries of \(\mathbf{r}_j\), so this shows that \(\langle A, A\rangle\) is the sum of the squares of all \(\mathrm{nm}\) entries of \(A\). Axiom P5 follows.
The next example is important in analysis.
Let \(\mathbf{C}[a, b]\) denote the vector space of continuous functions from \([a, b]\) to \(\mathbb{R}\), a subspace of \(\mathbf{F}[a\), \(b]\). Show that
\[
\langle f, g\rangle=\int_a^b f(x) g(x) d x
\]
defines an inner product on \(\mathbf{C}[a, b]\). \({ }^2\)
Solution
Axioms P1 and P2 are clear. As to axiom P4,
\[
\langle r f, g\rangle=\int_a^b r f(x) g(x) d x=r \int_a^b f(x) g(x) d x=r\langle f, g\rangle
\]
Axiom \(\mathrm{P} 3\) is similar. Finally, theorems of calculus show that \(\langle f, f\rangle=\int_a^b f(x)^2 d x \geq 0\) and, if \(f\) is continuous, that this is zero if and only if \(f\) is the zero function. This gives axiom P5.
If \(\mathbf{v}\) is any vector, then, using axiom \(\mathrm{P} 3\), we get
\[
\langle\mathbf{0}, \mathbf{v}\rangle=\langle\mathbf{0}+\mathbf{0}, \mathbf{v}\rangle=\langle\mathbf{0}, \mathbf{v}\rangle+\langle\mathbf{0}, \mathbf{v}\rangle
\]
and it follows that the number \(\langle\mathbf{0}, \mathbf{v}\rangle\) must be zero. This observation is recorded for reference in the following theorem, along with several other properties of inner products. The other proofs are left as Exercise 20.
\({ }^2\) This example (and others later that refer to it) can be omitted with no loss of continuity by students with no calculus background.
Let \(\langle\), \(\rangle\) be an inner product on a space \(V\); let \(\mathbf{v}, \boldsymbol{u}\), and \(\mathbf{w}\) denote vectors in \(V\); and let \(r\) denote a real number.
1. \(\langle\boldsymbol{u}, \boldsymbol{v}+\boldsymbol{w}\rangle=\langle\mathbf{u}, \mathbf{v}\rangle+\langle\mathbf{u}, \boldsymbol{w}\rangle\).
2. \(\langle\boldsymbol{v}, r \boldsymbol{w}\rangle=r\langle\mathbf{v}, \boldsymbol{w}\rangle=\langle\mathbf{r v}, \boldsymbol{w}\rangle\).
3. \(\langle\boldsymbol{v}, \boldsymbol{0}\rangle=0=\langle\boldsymbol{0}, \boldsymbol{v}\rangle\).
4. \(\langle\boldsymbol{v}, \mathbf{v}\rangle=0\) if and only if \(\mathbf{v}=\mathbf{0}\).
If \(\langle\),\(\rangle\) is an inner product on a space \(V\), then, given \(\mathbf{u}, \mathbf{v}\), and \(\mathbf{w}\) in \(V\),
\[
\langle r \mathbf{u}+s \mathbf{v}, \mathbf{w}\rangle=\langle r \mathbf{u}, \mathbf{w}\rangle+\langle s \mathbf{v}, \mathbf{w}\rangle=r\langle\mathbf{u}, \mathbf{w}\rangle+s\langle\mathbf{v}, \mathbf{w}\rangle
\]
for all \(r\) and \(s\) in \(\mathbb{R}\) by axioms \(\mathrm{P} 3\) and \(\mathrm{P} 4\). Moreover, there is nothing special about the fact that there are two terms in the linear combination or that it is in the first component:
\[
\left\langle r_1 \mathbf{v}_1+r_2 \mathbf{v}_2+\cdots+r_n \mathbf{v}_n, \mathbf{w}\right\rangle=r_1\left\langle\mathbf{v}_1, \mathbf{w}\right\rangle+r_2\left\langle\mathbf{v}_2, \mathbf{w}\right\rangle+\cdots+r_n\left\langle\mathbf{v}_n, \mathbf{w}\right\rangle
\]
and
\[
\left\langle\mathbf{v}, s_1 \mathbf{w}_1+s_2 \mathbf{w}_2+\cdots+s_m \mathbf{w}_m\right\rangle=s_1\left\langle\mathbf{v}, \mathbf{w}_1\right\rangle+s_2\left\langle\mathbf{v}, \mathbf{w}_2\right\rangle+\cdots+s_m\left\langle\mathbf{v}, \mathbf{w}_m\right\rangle
\]
hold for all \(r_i\) and \(s_i\) in \(\mathbb{R}\) and all \(\mathbf{v}, \mathbf{w}, \mathbf{v}_i\), and \(\mathbf{w}_j\) in \(V\). These results are described by saying that inner products "preserve" linear combinations. For example,
\[
\begin{aligned}
\langle 2 \mathbf{u}-\mathbf{v}, 3 \mathbf{u}+2 \mathbf{v}\rangle & =\langle 2 \mathbf{u}, 3 \mathbf{u}\rangle+\langle 2 \mathbf{u}, 2 \mathbf{v}\rangle+\langle-\mathbf{v}, 3 \mathbf{u}\rangle+\langle-\mathbf{v}, 2 \mathbf{v}\rangle \\
& =6\langle\mathbf{u}, \mathbf{u}\rangle+4\langle\mathbf{u}, \mathbf{v}\rangle-3\langle\mathbf{v}, \mathbf{u}\rangle-2\langle\mathbf{v}, \mathbf{v}\rangle \\
& =6\langle\mathbf{u}, \mathbf{u}\rangle+\langle\mathbf{u}, \mathbf{v}\rangle-2\langle\mathbf{v}, \mathbf{v}\rangle
\end{aligned}
\]
If \(A\) is a symmetric \(n \times n\) matrix and \(\mathbf{x}\) and \(\mathbf{y}\) are columns in \(\mathbb{R}^n\), we regard the \(1 \times 1\) matrix \(\mathbf{x}^T A \mathbf{y}\) as a number. If we write
\[
\langle\mathbf{x}, \mathbf{y}\rangle=\mathbf{x}^T A \mathbf{y} \quad \text { for all columns } \mathbf{x}, \mathbf{y} \text { in } \mathbb{R}^n
\]
then axioms \(\mathrm{P} 1-\mathrm{P} 4\) follow from matrix arithmetic (only \(\mathrm{P} 2\) requires that \(A\) is symmetric). Axiom \(\mathrm{P} 5\) reads
\[
\mathbf{x}^T A \mathbf{x}>0 \quad \text { for all columns } \mathbf{x} \neq \mathbf{0} \text { in } \mathbb{R}^n
\]
and this condition characterizes the positive definite matrices (Theorem 8.3.2). This proves the first assertion in the next theorem.
If \(A\) is any \(n \times n\) positive definite matrix, then
\[
\langle\mathbf{x}, \boldsymbol{y}\rangle=\mathbf{x}^T A \mathbf{y} \text { for all columns } \mathbf{x}, \mathbf{y} \text { in } \mathbb{R}^n
\]
defines an inner product on \(\mathbb{R}^n\), and every inner product on \(\mathbb{R}^n\) arises in this way.
Proof. Given an inner product \(\langle\),\(\rangle on \mathbb{R}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be the standard basis of \(\mathbb{R}^n\). If \(\mathbf{x}=\sum_{i=1}^n x_i \mathbf{e}_i\) and \(\mathbf{y}=\sum_{j=1}^n y_j \mathbf{e}_j\) are two vectors in \(\mathbb{R}^n\), compute \(\langle\mathbf{x}, \mathbf{y}\rangle\) by adding the inner product of each term \(x_i \mathbf{e}_i\) to each term \(y_j \mathbf{e}_j\). The result is a double sum.
\[
\langle\mathbf{x}, \mathbf{y}\rangle=\sum_{i=1}^n \sum_{j=1}^n\left\langle x_i \mathbf{e}_i, y_j \mathbf{e}_j\right\rangle=\sum_{i=1}^n \sum_{j=1}^n x_i\left\langle\mathbf{e}_i, \mathbf{e}_j\right\rangle y_j
\]
As the reader can verify, this is a matrix product:
\[
\langle\mathbf{x}, \mathbf{y}\rangle=\left[\begin{array}{llll}
x_1 & x_2 & \cdots & x_n
\end{array}\right]\left[\begin{array}{cccc}
\left\langle\mathbf{e}_1, \mathbf{e}_1\right\rangle & \left\langle\mathbf{e}_1, \mathbf{e}_2\right\rangle & \cdots & \left\langle\mathbf{e}_1, \mathbf{e}_n\right\rangle \\
\left\langle\mathbf{e}_2, \mathbf{e}_1\right\rangle & \left\langle\mathbf{e}_2, \mathbf{e}_2\right\rangle & \cdots & \left\langle\mathbf{e}_2, \mathbf{e}_n\right\rangle \\
\vdots & \vdots & \cdots & \vdots \\
\left\langle\mathbf{e}_n, \mathbf{e}_1\right\rangle & \left\langle\mathbf{e}_n, \mathbf{e}_2\right\rangle & \cdots & \left\langle\mathbf{e}_n, \mathbf{e}_n\right\rangle
\end{array}\right]\left[\begin{array}{c}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{array}\right]
\]
Hence \(\langle\mathbf{x}, \mathbf{y}\rangle=\mathbf{x}^T A \mathbf{y}\), where \(A\) is the \(n \times n\) matrix whose \((i, j)\)-entry is \(\left\langle\mathbf{e}_i, \mathbf{e}_j\right\rangle\). The fact that \(\left\langle\mathbf{e}_i, \mathbf{e}_j\right\rangle=\left\langle\mathbf{e}_j\right.\), \(\left.\mathbf{e}_i\right\rangle\) shows that \(A\) is symmetric. Finally, \(A\) is positive definite by Theorem 8.3.2.
Thus, just as every linear operator \(\mathbb{R}^n \rightarrow \mathbb{R}^n\) corresponds to an \(n \times n\) matrix, every inner product on \(\mathbb{R}^n\) corresponds to a positive definite \(n \times n\) matrix. In particular, the dot product corresponds to the identity matrix \(I_n\).
Remark
If we refer to the inner product space \(\mathbb{R}^n\) without specifying the inner product, we mean that the dot product is to be used.
Let the inner product \(\langle\),\(\rangle be defined on \mathbb{R}^2\) by
\[
\left\langle\left[\begin{array}{l}
v_1 \\
v_2
\end{array}\right],\left[\begin{array}{l}
w_1 \\
w_2
\end{array}\right]\right\rangle=2 v_1 w_1-v_1 w_2-v_2 w_1+v_2 w_2
\]
Find a symmetric \(2 \times 2\) matrix \(A\) such that \(\langle\mathbf{x}, \mathbf{y}\rangle=\mathbf{x}^T A \mathbf{y}\) for all \(\mathbf{x}, \mathbf{y}\) in \(\mathbb{R}^2\).
Solution
The \((i, j)\)-entry of the matrix \(A\) is the coefficient of \(v_i w_j\) in the expression, so \(A=\) \(\left[\begin{array}{rr}2 & -1 \\ -1 & 1\end{array}\right]\). Incidentally, if \(\mathbf{x}=\left[\begin{array}{l}x \\ y\end{array}\right]\), then
\[
\langle\mathbf{x}, \mathbf{x}\rangle=2 x^2-2 x y+y^2=x^2+(x-y)^2 \geq 0
\]
for all \(\mathbf{x}\), so \(\langle\mathbf{x}, \mathbf{x}\rangle=0\) implies \(\mathbf{x}=\mathbf{0}\). Hence \(\langle\),\(\rangle\) is indeed an inner product, so \(A\) is positive definite.
Let \(\langle\),\(\rangle\) be an inner product on \mathbb{R}^n\) given as in Theorem 10.1.2 by a positive definite matrix \(A\). If \(\mathbf{x}=\left[\begin{array}{llll}x_1 & x_2 & \cdots & x_n\end{array}\right]^T\), then \(\langle\mathbf{x}, \mathbf{x}\rangle=\mathbf{x}^T A \mathbf{x}\) is an expression in the variables \(x_1, x_2, \ldots, x_n\) called a quadratic form. These are studied in detail in Section 8.8.
As in \(\mathbb{R}^n\), if \(\langle\),\(\rangle is an inner product on a space V\), the \(\mathbf{n o r m}^3\|\mathbf{v}\|\) of a vector \(\mathbf{v}\) in \(V\) is defined by
\[
\|\mathbf{v}\|=\sqrt{\langle\mathbf{v}, \mathbf{v}\rangle}
\]
We define the distance between vectors \(\mathbf{v}\) and \(\mathbf{w}\) in an inner product space \(V\) to be
\[
\mathrm{d}(\mathbf{v}, \boldsymbol{w})=\|\mathbf{v}-\boldsymbol{w}\|
\]
Note that axiom P5 guarantees that \(\langle\mathbf{v}, \mathbf{v}\rangle \geq 0\), so \(\|\mathbf{v}\|\) is a real number.
The norm of a continuous function \(f=f(x)\) in \(\mathbf{C}[a, b]\) (with the inner product from Example 10.1.3) is given by
\[
\|f\|=\sqrt{\int_a^b f(x)^2 d x}
\]
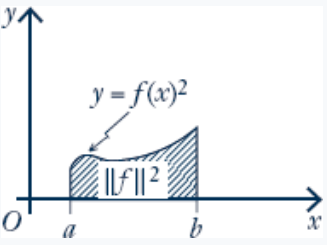
Hence \(\|f\|^2\) is the area beneath the graph of \(y=f(x)^2\) between \(x=a\) and \(x=b\) (see the diagram).
Show that \(\langle\mathbf{u}+\mathbf{v}, \mathbf{u}-\mathbf{v}\rangle=\|\mathbf{u}\|^2-\|\mathbf{v}\|^2\) in any inner product space.
Solution
\[
\begin{aligned}
\langle\mathbf{u}+\mathbf{v}, \mathbf{u}-\mathbf{v}\rangle & =\langle\mathbf{u}, \mathbf{u}\rangle-\langle\mathbf{u}, \mathbf{v}\rangle+\langle\mathbf{v}, \mathbf{u}\rangle-\langle\mathbf{v}, \mathbf{v}\rangle \\
& =\|\mathbf{u}\|^2-\langle\mathbf{u}, \mathbf{v}\rangle+\langle\mathbf{u}, \mathbf{v}\rangle-\|\mathbf{v}\|^2 \\
& =\|\mathbf{u}\|^2-\|\mathbf{v}\|^2
\end{aligned}
\]
A vector \(\mathbf{v}\) in an inner product space \(V\) is called a unit vector if \(\|\mathbf{v}\|=1\). The set of all unit vectors in \(V\) is called the unit ball in \(V\). For example, if \(V=\mathbb{R}^2\) (with the dot product) and \(\mathbf{v}=(x, y\) ), then
\[
\|\mathbf{v}\|^2=1 \quad \text { if and only if } \quad x^2+y^2=1
\]
Hence the unit ball in \(\mathbb{R}^2\) is the unit circle \(x^2+y^2=1\) with centre at the origin and radius 1 . However, the shape of the unit ball varies with the choice of inner product.
\({ }^3\) If the dot product is used in \(\mathbb{R}^n\), the norm \(\|\mathbf{x}\|\) of a vector \(\mathbf{x}\) is usually called the length of \(\mathbf{x}\).
Let \(a>0\) and \(b>0\). If \(\mathbf{v}=(x, y)\) and \(\mathbf{w}=\left(x_1, y_1\right)\), define an inner product on \(\mathbb{R}^2\) by
\[
\langle\mathbf{v}, \mathbf{w}\rangle=\frac{x x_1}{a^2}+\frac{y y_1}{b^2}
\]
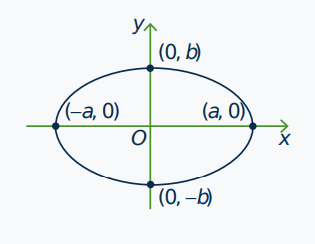
The reader can verify (Exercise 5) that this is indeed an inner product. In this case
\[
\|\mathbf{v}\|^2=1 \quad \text { if and only if } \quad \frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\]
so the unit ball is the ellipse shown in the diagram.
Example 10.1.7 graphically illustrates the fact that norms and distances in an inner product space \(V\) vary with the choice of inner product in \(V\).
If \(\mathbf{v} \neq \boldsymbol{0}\) is any vector in an inner product space \(V\), then \(\frac{1}{\|\mathbf{v}\|} \mathbf{V}\) is the unique unit vector that is a positive multiple of \(\mathbf{v}\).
The next theorem reveals an important and useful fact about the relationship between norms and inner products, extending the Cauchy inequality for \(\mathbb{R}^n\) (Theorem 5.3.2).
If \(\mathbf{v}\) and \(\mathbf{w}\) are two vectors in an inner product space \(V\), then
\[
\langle\mathbf{v}, \boldsymbol{w}\rangle^2 \leq\|\mathbf{v}\|^2\|\boldsymbol{w}\|^2
\]
Moreover, equality occurs if and only if one of \(\mathbf{v}\) and \(\mathbf{w}\) is a scalar multiple of the other.
Proof. Write \(\|\mathbf{v}\|=a\) and \(\|\mathbf{w}\|=b\). Using Theorem 10.1.1 we compute:
\[
\begin{aligned}
\|b \mathbf{v}-a \mathbf{w}\|^2 & =b^2\|\mathbf{v}\|^2-2 a b\langle\mathbf{v}, \mathbf{w}\rangle+a^2\|\mathbf{w}\|^2=2 a b(a b-\langle\mathbf{v}, \mathbf{w}\rangle) \\
\|b \mathbf{v}+a \mathbf{w}\|^2 & =b^2\|\mathbf{v}\|^2+2 a b\langle\mathbf{v}, \mathbf{w}\rangle+a^2\|\mathbf{w}\|^2=2 a b(a b+\langle\mathbf{v}, \mathbf{w}\rangle)
\end{aligned}
\]
It follows that \(a b-\langle\mathbf{v}, \mathbf{w}\rangle \geq 0\) and \(a b+\langle\mathbf{v}, \mathbf{w}\rangle \geq 0\), and hence that \(-a b \leq\langle\mathbf{v}, \mathbf{w}\rangle \leq a b\). But then \(\mid\langle\mathbf{v}, \mathbf{w}\) \rangle \(\mid \leq a b=\|\mathbf{v}\|\|\mathbf{w}\|\), as desired.
Conversely, if \(|\langle\mathbf{v}, \mathbf{w}\rangle|=\|\mathbf{v}\|\|\mathbf{w}\|=a b\) then \(\langle\mathbf{v}, \mathbf{w}\rangle= \pm a b\). Hence (10.1) shows that \(b \mathbf{v}-a \mathbf{w}=\mathbf{0}\) or \(b \mathbf{v}+a \mathbf{w}=\mathbf{0}\). It follows that one of \(\mathbf{v}\) and \(\mathbf{w}\) is a scalar multiple of the other, even if \(a=0\) or \(b=0\).
\({ }^4\) Hermann Amandus Schwarz (1843-1921) was a German mathematician at the University of Berlin. He had strong geometric intuition, which he applied with great ingenuity to particular problems. A version of the inequality appeared in 1885.
If \(f\) and \(g\) are continuous functions on the interval \([a, b]\), then (see Example 10.1.3)
\[
\left\{\int_a^b f(x) g(x) d x\right\}^2 \leq \int_a^b f(x)^2 d x \int_a^b g(x)^2 d x
\]
Another famous inequality, the so-called triangle inequality, also comes from the Cauchy-Schwarz inequality. It is included in the following list of basic properties of the norm of a vector.
Theorem 10.1.5
If \(V\) is an inner product space, the norm \(\|\cdot\|\) has the following properties.
1. \(\|\boldsymbol{v}\| \geq 0\) for every vector \(\mathbf{v}\) in \(V\).
2. \(\|\boldsymbol{v}\|=0\) if and only if \(\mathbf{v}=\mathbf{0}\).
3. \(\|r \mathbf{v}\|=|r|\|\mathbf{v}\|\) for every \(\mathbf{v}\) in \(V\) and every \(r\) in \(\mathbb{R}\).
4. \(\|\boldsymbol{v}+\boldsymbol{w}\| \leq\|\mathbf{v}\|+\|\boldsymbol{w}\|\) for all \(\mathbf{v}\) and \(\mathbf{w}\) in \(V\) (triangle inequality).
Proof. Because \(\|\mathbf{v}\|=\sqrt{\langle\mathbf{v}, \mathbf{v}\rangle}\), properties (1) and (2) follow immediately from (3) and (4) of Theorem 10.1.1. As to (3), compute
\[
\|r \mathbf{v}\|^2=\langle r \mathbf{v}, r \mathbf{v}\rangle=r^2\langle\mathbf{v}, \mathbf{v}\rangle=r^2\|\mathbf{v}\|^2
\]
Hence (3) follows by taking positive square roots. Finally, the fact that \(\langle\mathbf{v}, \mathbf{w}\rangle \leq\|\mathbf{v}\|\|\mathbf{w}\|\) by the CauchySchwarz inequality gives
\[
\begin{aligned}
\|\mathbf{v}+\mathbf{w}\|^2=\langle\mathbf{v}+\mathbf{w}, \mathbf{v}+\mathbf{w}\rangle & =\|\mathbf{v}\|^2+2\langle\mathbf{v}, \mathbf{w}\rangle+\|\mathbf{w}\|^2 \\
& \leq\|\mathbf{v}\|^2+2\|\mathbf{v}\|\|\mathbf{w}\|+\|\mathbf{w}\|^2 \\
& =(\|\mathbf{v}\|+\|\mathbf{w}\|)^2
\end{aligned}
\]
Hence (4) follows by taking positive square roots.
It is worth noting that the usual triangle inequality for absolute values,
\[
|r+s| \leq|r|+|s| \text { for all real numbers } r \text { and } s,
\]
is a special case of (4) where \(V=\mathbb{R}=\mathbb{R}^1\) and the dot product \(\langle r, s\rangle=r s\) is used.
In many calculations in an inner product space, it is required to show that some vector \(\mathbf{v}\) is zero. This is often accomplished most easily by showing that its norm \(\|\mathbf{v}\|\) is zero. Here is an example.
Let \(\left\{\mathbf{v}_1, \ldots, \mathbf{v}_n\right\}\) be a spanning set for an inner product space \(V\). If \(\mathbf{v}\) in \(V\) satisfies \(\left\langle\mathbf{v}, \mathbf{v}_i\right\rangle=0\) for each \(i=1,2, \ldots, n\), show that \(\mathbf{v}=\mathbf{0}\).
Solution
Write \(\mathbf{v}=r_1 \mathbf{v}_1+\cdots+r_n \mathbf{v}_n, r_i\) in \(\mathbb{R}\). To show that \(\mathbf{v}=\mathbf{0}\), we show that \(\|\mathbf{v}\|^2=\langle\mathbf{v}, \mathbf{v}\rangle=0\).
Compute:
\[
\langle\mathbf{v}, \mathbf{v}\rangle=\left\langle\mathbf{v}, r_1 \mathbf{v}_1+\cdots+r_n \mathbf{v}_n\right\rangle=r_1\left\langle\mathbf{v}, \mathbf{v}_1\right\rangle+\cdots+r_n\left\langle\mathbf{v}, \mathbf{v}_n\right\rangle=0
\]
by hypothesis, and the result follows.
The norm properties in Theorem 10.1.5 translate to the following properties of distance familiar from geometry. The proof is Exercise 21.
Let \(V\) be an inner product space.
1. \(d(\boldsymbol{v}, \mathbf{w}) \geq 0\) for all \(\mathbf{v}, \boldsymbol{w}\) in \(V\).
2. \(d(\boldsymbol{v}, \mathbf{w})=0\) if and only if \(\mathbf{v}=\mathbf{w}\).
3. \(d(\mathbf{v}, \mathbf{w})=d(\mathbf{w}, \mathbf{v})\) for all \(\mathbf{v}\) and \(\mathbf{w}\) in \(V\).
4. \(d(\boldsymbol{v}, \boldsymbol{w}) \leq d(\mathbf{v}, \boldsymbol{u})+d(\mathbf{u}, \boldsymbol{w})\) for all \(\mathbf{v}, \boldsymbol{u}\), and \(\boldsymbol{w}\) in \(V\).


