7.5: Inverse Matrix
- Page ID
- 1963
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Definition
A square matrix \(M\) is \(\textit{invertible}\) (or \(\textit{nonsingular}\)) if there exists a matrix \(M^{-1}\) such that
\[M^{-1}M=I=MM^{-1}.\]
If \(M\) has no inverse, we say \(M\) is \(\textit{Singular}\) or \(\textit{non-invertible}\).

Remark
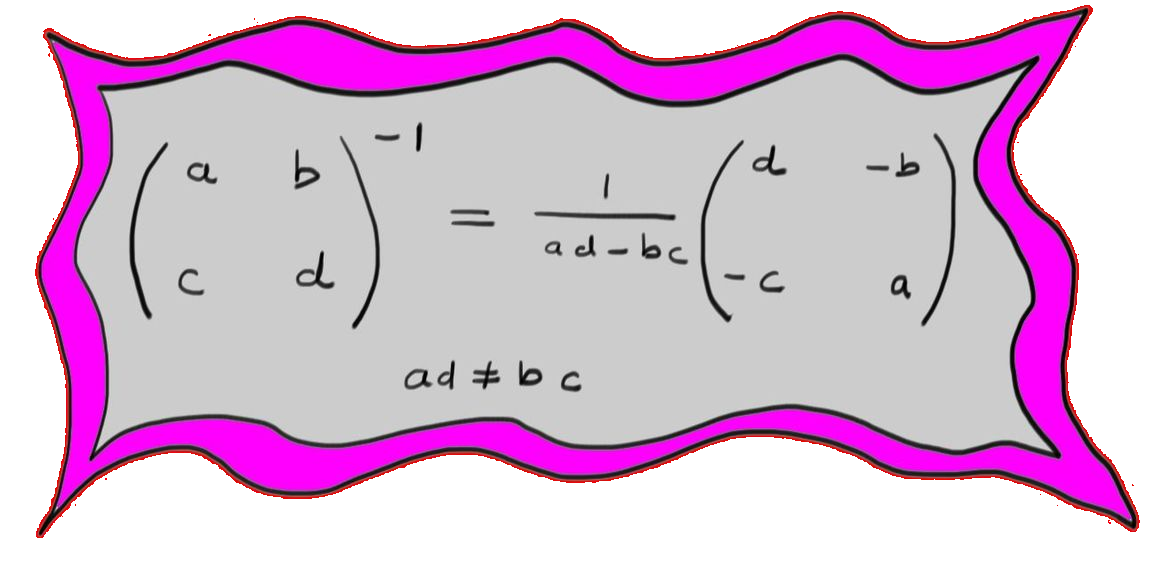
Let \(M\) and \(N\) be the matrices:
\[
M=\begin{pmatrix}
a & b \\
c & d \\
\end{pmatrix},\qquad N=\begin{pmatrix}
d & -b \\
-c & a \\
\end{pmatrix}
\]
Multiplying these matrices gives:
\[
MN=\begin{pmatrix}
ad-bc & 0 \\
0 & ad-bc \\
\end{pmatrix}=(ad-bc)I\, .
\]
Then \(M^{-1}=\frac{1}{ad-bc}\begin{pmatrix}
d & -b \\
-c & a \\
\end{pmatrix}\), so long as \(ad-bc\neq 0\).
Three Properties of the Inverse
1. If \(A\) is a square matrix and \(B\) is the inverse of \(A\), then \(A\) is the inverse of \(B\), since \(AB=I=BA\). So we have the identity:
\[
(A^{-1})^{-1}=A
\]
2. Notice that \(B^{-1}A^{-1}AB=B^{-1}IB=I=ABB^{-1}A^{-1}\).
Then:
\[(AB)^{-1}=B^{-1}A^{-1}\]
Thus, much like the transpose, taking the inverse of a product \(\textit{reverses}\) the order of the product.
3. Finally, recall that \((AB)^{T}=B^{T}A^{T}\). Since \(I^{T}=I\), then \((A^{-1}A)^{T}=A^{T}(A^{-1})^{T}=I\). Similarly, \((AA^{-1})^{T}=(A^{-1})^{T}A^{T}=I\). Then:
\[
(A^{-1})^{T}=(A^T)^{-1}
\]
Finding Inverses (Redux)
Gaussian elimination can be used to find inverse matrices. This concept is covered in chapter 2, section 2.3.2, but is presented here again as review.
Suppose \(M\) is a square invertible matrix and \(MX=V\) is a linear system. The solution must be unique because it can be found by multiplying the equation on both sides by \(M^{-1}\) yielding \(X=M^{-1}V\). Thus, the reduced row echelon form of the linear system has an identity matrix on the left:
\[
\begin{amatrix}{rr}
M & V
\end{amatrix}
\sim
\begin{amatrix}{rr}
I & M^{-1}V
\end{amatrix}
\]
Solving the linear system \(MX=V\) then tells us what \(M^{-1}V\) is.
To solve many linear systems with the same matrix at once,
\[MX=V_{1},~MX=V_{2}\]
we can consider augmented matrices with many columns on the right and then apply Gaussian row reduction to the left side of the matrix. Once the identity matrix is on the left side of the augmented matrix, then the solution of each of the individual linear systems is on the right.
\[
\left(\begin{array}{c|cc}
\!M & V_{1}&V_{2}\!
\end{array}\right)
\sim
\left(\begin{array}{c|cc}
\!I & M^{-1}V_{1} & M^{-1}V_{2}\!
\end{array}\right)
\]
To compute \(M^{-1}\), we would like \(M^{-1}\), rather than \(M^{-1}V\) to appear on the right side of our augmented matrix. This is achieved by solving the collection of systems \(MX=e_{k}\), where \(e_{k}\) is the column vector of zeroes with a \(1\) in the \(k\)th entry. i.e. the \(n \times n\) identity matrix can be viewed as a bunch of column vectors \(I_{n}=(e_{1} \ e_{2} \ \cdots e_{n})\). So, putting the \(e_{k}\)'s together into an identity matrix, we get:
\[
\begin{amatrix}{1}
M & I
\end{amatrix}
\sim
\begin{amatrix}{1}
I & M^{-1}I
\end{amatrix}
=\begin{amatrix}{1}
I & M^{-1}
\end{amatrix}
\]
Example \(\PageIndex{1}\):
Find \(\begin{pmatrix}
-1 & 2 & -3 \\
2 & 1 & 0 \\
4 & -2 & 5 \\
\end{pmatrix}^{-1}
\).
We start by writing the augmented matrix, then apply row reduction to the left side.
\begin{eqnarray*}
\left(\begin{array}{rrr|ccc}
-1 & 2 & -3 & 1 & 0 & 0 \\
2 & 1 & 0 & 0 & 1 & 0 \\
4 & -2 & 5 & 0 & 0 & 1 \\
\end{array}\right) & \sim & \left(\begin{array}{crr|ccc}
1 & -2& 3 & 1 & 0 & 0 \\
0 & 5 & -6 & 2 & 1 & 0 \\
0 & 6 & -7 & 4 & 0 & 1 \\
\end{array}\right) \\
& \sim & \left(\begin{array}{ccr|rrc}
1 & 0 & \frac{3}{5} & -\frac{1}{4} & \frac{2}{5} & 0 \\
0 & 1 & -\frac{6}{5} & \frac{2}{5} & \frac{1}{5} & 0 \\
0 & 0 & \frac{1}{5} & \frac{4}{5} & -\frac{6}{5} & 1 \\
\end{array}\right) \\
& \sim & \left(\begin{array}{ccc|rrr}
1 & 0 & 0 & -5 & 4 & -3 \\
0 & 1 & 0 & 10 & -7 & 6 \\
0 & 0 & 1 & 8 & -6 & 5 \\
\end{array}\right) \\
\end{eqnarray*}
At this point, we know \(M^{-1}\) assuming we didn't goof up. However, row reduction is a lengthy and arithmetically involved process, so we should \(\textit{check our answer,}\) by confirming that \(MM^{-1}=I\) (or if you prefer \(M^{-1}M=I\)):
\[MM^{-1} =
\begin{pmatrix}
-1 & 2 & -3 \\
2 & 1 & 0 \\
4 & -2 & 5 \\
\end{pmatrix}\begin{pmatrix}
-5 & 4 & -3 \\
10 & -7 & 6 \\
8 & -6 & 5 \\
\end{pmatrix}
=\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
\]
The product of the two matrices is indeed the identity matrix, so we're done.
Linear Systems and Inverses
If \(M^{-1}\) exists and is known, then we can immediately solve linear systems associated to \(M\).
Example \(\PageIndex{12}\):
Consider the linear system:
\[
\begin{array}{r}
-x & +2y & -3z &=& 1 \\
2x & +\ y\, & &=& 2 \\
4x & -2y & +5z &=& 0
\end{array}
\]
The associated matrix equation is \(MX=\begin{pmatrix}1\\2\\0\end{pmatrix},\) where \(M\) is the same as in the previous section. Then:
\[
\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}
-1 & 2 & -3 \\
2 & 1 & 0 \\
4 & -2 & 5 \\
\end{pmatrix}^{-1}\begin{pmatrix}1\\2\\0\end{pmatrix}
=\begin{pmatrix}
-5 & 4 & -3 \\
10 & -7 & 6 \\
8 & -6 & 5 \\
\end{pmatrix}\begin{pmatrix}1\\2\\0\end{pmatrix}
=\begin{pmatrix}3\\-4\\-4\end{pmatrix}
\]
Then \(\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}3\\-4\\-4\end{pmatrix}\). In summary, when \(M^{-1}\) exists, then $$MX=V \Leftrightarrow X=M^{-1}V\, .\]
Homogeneous Systems
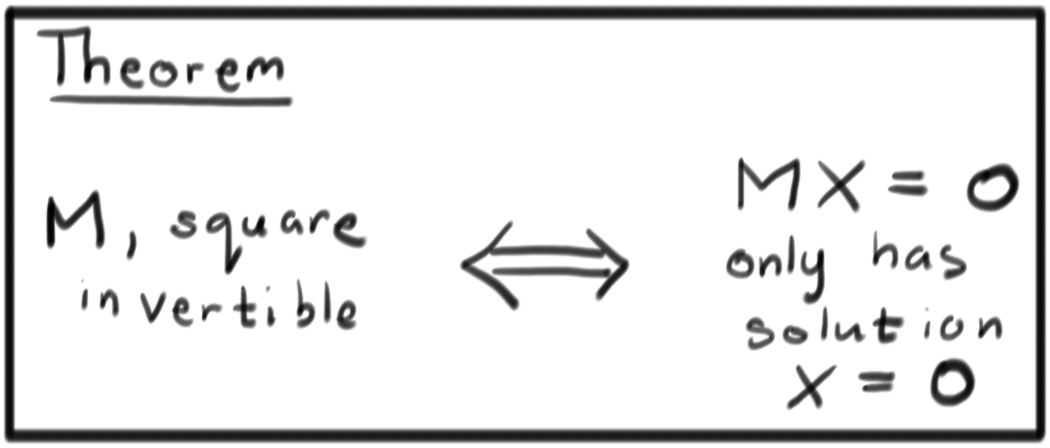
Theorem
A square matrix \(M\) is invertible if and only if the homogeneous system $$MX=0$$ has no non-zero solutions.
Proof
First, suppose that \(M^{-1}\) exists. Then \(MX=0 \Rightarrow X=M^{-1}0=0\). Thus, if \(M\) is invertible, then \(MX=0\) has no non-zero solutions.
On the other hand, \(MX=0\) always has the solution \(X=0\). If no other solutions exist, then \(M\) can be put into reduced row echelon form with every variable a pivot. In this case, \(M^{-1}\) can be computed using the process in the previous section.
Bit Matrices
In computer science, information is recorded using binary strings of data. For example, the following string contains an English word:
\[ 011011000110100101101110011001010110000101110010 \]
A bit is the basic unit of information, keeping track of a single one or zero. Computers can add and multiply individual bits very quickly.
In chapter 5, section 5.2 it is explained how to formulate vector spaces over fields other than real numbers. In particular, for the vectors space make sense with numbers \(Z_{2}=\{0,1 \}\) with addition and multiplication given by:
\[
\begin{array}{c|cc}
+ & 0 & 1 \\ \hline
0 & 0 & 1 \\
1 & 1 & 0 \\
\end{array}
\qquad
\begin{array}{c|cc}
\times& 0 & 1 \\ \hline
0 & 0 & 0 \\
1 & 0 & 1 \\
\end{array}
\label{Z2}\]
Notice that \(-1=1\), since \(1+1=0\). Therefore, we can apply all of the linear algebra we have learned thus far to matrices with \(Z_{2}\) entries. A matrix with entries in \(Z_{2}\) is sometimes called a \(\textit{bit matrix}\).
Example \(\PageIndex{3}\):
\(\begin{pmatrix}
1 & 0 & 1 \\
0 & 1 & 1 \\
1 & 1 & 1 \\
\end{pmatrix}\) is an invertible matrix over \(Z_{2}\):
\[\begin{pmatrix}
1 & 0 & 1 \\
0 & 1 & 1 \\
1 & 1 & 1 \\
\end{pmatrix}^{-1}=\begin{pmatrix}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 1 \\
\end{pmatrix}
\]
This can be easily verified by multiplying:
\[\begin{pmatrix}
1 & 0 & 1 \\
0 & 1 & 1 \\
1 & 1 & 1 \\
\end{pmatrix}\begin{pmatrix}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 1 \\
\end{pmatrix}=\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
\]
Application: Cryptography
A very simple way to hide information is to use a substitution cipher, in which the alphabet is permuted and each letter in a message is systematically exchanged for another. For example, the ROT-13 cypher just exchanges a letter with the letter thirteen places before or after it in the alphabet. For example, HELLO becomes URYYB. Applying the algorithm again decodes the message, turning URYYB back into HELLO. Substitution ciphers are easy to break, but the basic idea can be extended to create cryptographic systems that are practically uncrackable. For example, a \(\textit{one-time pad}\) is a system that uses a different substitution for each letter in the message. So long as a particular set of substitutions is not used on more than one message, the one-time pad is unbreakable.
English characters are often stored in computers in the ASCII format. In ASCII, a single character is represented by a string of eight bits, which we can consider as a vector in \(Z_{2}^{8}\) (which is like vectors in \(\Re^{8}\), where the entries are zeros and ones). One way to create a substitution cipher, then, is to choose an \(8\times 8\) invertible bit matrix \(M\), and multiply each letter of the message by \(M\). Then to decode the message, each string of eight characters would be multiplied by \(M^{-1}\).
To make the message a bit tougher to decode, one could consider pairs (or longer sequences) of letters as a single vector in \(Z_{2}^{16}\) (or a higher-dimensional space), and then use an appropriately-sized invertible matrix. For more on cryptography, see "The Code Book,'' by Simon Singh (1999, Doubleday).
Contributor
David Cherney, Tom Denton, and Andrew Waldron (UC Davis)


