10: Linear Independence
- Page ID
- 1732
Consider a plane \(P\) that includes the origin in \(\Re^{3}\) and a collection \(\{u,v,w\}\) of non-zero vectors in \(P\):
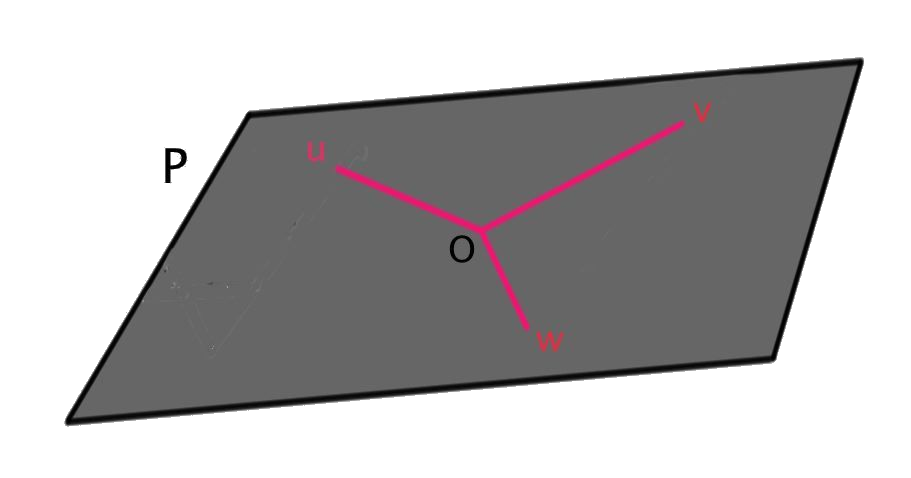
If no two of \(u, v\) and \(w\) are parallel, then \(P= span \{u,v,w\}\). But any two vectors determines a plane, so we should be able to span the plane using only two of the vectors \(u,v,w\). Then we could choose two of the vectors in \(\{u,v,w\}\) whose span is \(P\), and express the other as a linear combination of those two. Suppose \(u\) and \(v\) span \(P\). Then there exist constants \(d^{1}, d^{2}\) (not both zero) such that \(w=d^{1}u+d^{2}v\). Since \(w\) can be expressed in terms of \(u\) and \(v\) we say that it is not independent. More generally, the relationship
\[c^{1}u+c^{2}v+c^{3}w=0 \qquad c^{i} \in \Re, \textit{ some \(c^{i}\neq 0\)}\]
expresses the fact that \(u,v,w\) are not all independent.
Definition (Independent)
We say that the vectors \(v_{1}, v_{2}, \ldots, v_{n}\) are \(\textit{linearly dependent}\) if there exist constants (usually our vector spaces are defined over \(\mathbb{R}\), but in general we can have vector spaces defined over different base fields such as \(\mathbb{C}\) or \(\mathbb{Z}_{2}\). The coefficients \(c^{i}\) should come from whatever our base field is (usually \(\mathbb{R}\)).} \(c^{1}, c^{2}, \ldots, c^{n}\) not all zero such that
\[c^{1}v_{1} + c^{2}v_{2}+ \cdots +c^{n}v_{n}=0.\]
Otherwise, the vectors \(v_{1}, v_{2}, \ldots, v_{n}\) are \(\textit{linearly independent.}\)
Remark
The zero vector \(0_{V}\) can \(\textit{never}\) be on a list of independent vectors because \(\alpha 0_{V}=0_{V}\) for any scalar \(\alpha\).
Example \(\PageIndex{1}\):
Consider the following vectors in \(\Re^{3}\):
\[
v_{1}=\begin{pmatrix}4\\-1\\3\end{pmatrix}, \qquad
v_{2}=\begin{pmatrix}-3\\7\\4\end{pmatrix}, \qquad
v_{3}=\begin{pmatrix}5\\12\\17\end{pmatrix}, \qquad
v_{4}=\begin{pmatrix}-1\\1\\0\end{pmatrix}.
\]
Are these vectors linearly independent?
No, since \(3v_{1}+2v_{2}-v_{3}+v_{4}=0\), the vectors are linearly \(\textit{dependent}\).
Contributor
David Cherney, Tom Denton, and Andrew Waldron (UC Davis)


