27.1: Orthogonal Complement

Last updated
Save as PDF

Page ID: 69429

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Definition

A vector \(u\) is orthogonal to a subspace \(W\) of \(R^n\) if \(u\) is orthogonal to any \(w\) in \(W\) (\(u \cdot w=0\) for all \(w \in W\)).

For example, consider the following figure, if we consider the plane to be a subspace then the perpendicular vector comming out of the plane is is orthoginal to any vector in the plane:

Definition

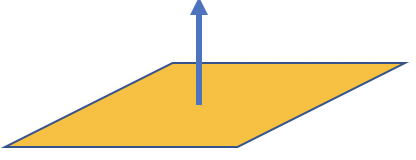
The orthogonal complement of \(W\) is the set of all vectors that are orthogonal to \(W\). The set is denoted as \(W_{\bot}\).

Question

Is \(W_{\bot}\) a subspace of \(R^n\)? Justify your answer briefly.

Question

What are the vectors in both \(W\) and \(W_{\bot}\)?

from IPython.display import YouTubeVideo
YouTubeVideo("5B8XluiqdHM",width=640,height=360, cc_load_policy=True)

Projection of a Vector onto a Subspace

Think of a projection onto a subspace is analogous to a shadow on a surface. Aspects of an objects 3D space is represented in a 2D shadow but you can’t take the shadow by itself and exactly recreate the 3D surface.

A bird made from hand shadows. — Image from: Wikimedia

The following is the matimatical defination of projection onto a subspace.

Definition

Let \(W\) be a subspace of \(R^n\) of dimension \(m\). Let \(\{w_1,\cdots,w_m\}\) be an orthonormal basis for \(W\). Then the projection of vector \(v\) in \(R^n\) onto \(W\) is denoted as \(\mbox{proj}_Wv\) and is defined as \(\mbox{proj}_Wv = (v\cdot w_1)w_1+(v\cdot w_2)w_2+\cdots+(v\cdot w_m)w_m\).

Another way to say the above defination is that the project of \(v\) onto the \(W\) is just the sumation of \(v\) projected onto each vector in a basis of \(W\).

Remarks:

Recall in the lecture on Projections, we discussed the projection onto a vector, which is the case for \(m=1\). We used the projection for \(m>1\) in the Gram-Schmidt algorithm.

The projection does not depend on which orthonormal basis you choose.

If \(v\) is in \(W\), we have \(\mbox{proj}_Wv=v\).

The Orthogonal Decomposition Theorem

Theorem

Let \(W\) be a subspace of \(R^n\). Every vector in \(v\) in \(R^n\) can be written uniquely in the form \(v = w+w_{\bot}\), where \(w\) is in \(W\) and \(w_{\bot}\) is orthogonal to \(W\) (i.e., \(w_{\bot}\) is in \(W_{\bot}\)). In addition, \(w=\mbox{proj}_Wv\) and \(w_{\bot} = v-\mbox{proj}_Wv\).

Definition

Let \(x\) be a point in \(R^n\), \(W\) be a subspace of \(R^n\). The distance from \(x\) to \(W\) is defined to be the minimum of the distances from \(x\) to any point \(y\) in \(W\). \(d(x,W)=\min \{\|x-y\|: \mbox{ for all }y \mbox{ in } W\}\). The optimal \(y\) can be achieved at \(\mbox{proj}_Wx\), and \(d(x,W)=|x-\mbox{proj}_Wx|\).

Question

Let \(v=(3,2,6)\) and \(W\) is the subspace consisting all vectors with the form \((a,b,b)\). Find the projection of \(v\) onto \(W\).

Question

Let \(v=(3,2,6)\) and \(W\) is the subspace consisting all vectors with the form \((a,b,b)\). Find the distance from \(v\) to \(W\).