Appendix D: List of Symbols

Symbol	Meaning
$\to$	Conditional statement
$\mathbb{R}$	set of real numbers
$\mathbb{Q}$	set of rational numbers
$\mathbb{Z}$	set of integers
$\mathbb{N}$	set of natural numbers
$y \in A$	$y$ is an element of $A$
$z \notin A$	$z$ is not an element of $A$
{ | }	set builder notation
$\forall$	universal quantifier
$\exists$	existential quantifier
$\emptyset$	the empty set
$\wedge$	conjunction
$vee$	disjunction
$\urcorner$	negation
$\leftrightarrow$	biconditional statement
$\equiv$	logically equivalent
$m\ |\ n$	$m$ divides $n$
$a \equiv b$ (mod $n$)	$a$ is congruent to $b$ modulo $n$
$|x|$	the absolute value of $x$
$A = B$	$A$ equals $B$ (set equality)
$A \subseteq B$	$A$ is a subset of $B$
$A \not\subseteq B$	$A$ is not a subset of $B$
$A \subset B$	$A$ is a proper subset of $B$
$\mathcal{P}(A)$	power set of $A$
$|A|$	cardinality of a finite set $A$
$A \cap B$	intersection of $A$ and $B$
$A^{c}$	complement of $A$
$A - B$	set difference of $A$ and $B$
$A \times B$	Cartesian product of $A$ and $B$
$(a, b)$	ordered pair
$\mathbb{R} \times \mathbb{R}$	Cartesian plane
$\mathbb{R}^2$	Cartesian plane
\(\bigcup_{X \in \mathcal{C} X\)	union of a family of sets
\(\bigcap_{X \in \mathcal{C} X\)	intersection of a finite family of sets
$\bigcup_{j = 1}^{n} A_j$	union of a finite family of sets
$\bigcap_{j = 1}^{n} A_j$	intersection of a finite family of sets
$\bigcup_{j = 1}^{\infty} B_j$	union of an infinite family of sets
$\bigcap_{j = 1}^{\infty} B_j$	intersection of a infinite family of sets
$\{A_{\alpha}\ |\ \alpha \in \Lambda\}$	indexed family of sets
$\bigcup_{\alpha \in \Lambda} A_{\alpha}$	union of an indexed family of sets
$\bigcap_{\alpha \in \Lambda} A_{\alpha}$	intersection of an indexed family of sets
$n!$	$n$ factorial
$f_1, f_2, f_3, ...$	Fibonacci numbers
$s(n)$	sum of the divisors of $n$
$f: A \to B$	function from $A$ to $B$
dom($f$)	domain of the function $f$
codom($f$)	codmain of the function $f$
$f(x)$	inage of $x$ under $f$
range($f$)	range of the function $f$
$d(n)$	number of divisors of $n$
$I_{A}$	identity function on the set $A$
$p_1, p_2$	projection functions
det$(A)$	determinant of $A$
$A^{T}$	transpose of $A$
det: $M_{2, 2} \to \mathbb{R}$	determinant function
$g \circ f: A \to C$	composition of function $f$ and $g$
$f^{-1}$	the inverse of the function $f$
Sin	the restricted sine function
Sin$^{-1}$	the inverse sine function
dom($R$)	domain of the relation $R$
range($R$)	range of the relation $R$
$x\ R\ y$	$x$ is related to $y$
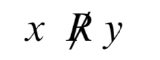	$x$ is not related to $y$
$x \sim y$	$x$ is related to $y$
$x \nsim y$	$x$ is not related to $y$
$R^{-1}$	the inverse of the relation $R$
$[a]$	equivalence class of $a$
$[a]$	congruence class of $a$
$\mathbb{Z}_{n}$	the integers modulo $n$
$[a] \oplus [c]$	addition in $\mathbb{Z}_{n}$
$[a] \odot [c]$	multiplication in $\mathbb{Z}_{n}$
gcd($a$, $b$)	greatest common divisor of $a$ and $b$
$f(A)$	image of $A$ under the function $f$
$f^{-1}(C)$	pre-image of $C$ under the funtion $f$
$A \thickapprox B$	$A$ is equivalent to $B$ $A$ and $B$ have the same cardinality
$\mathbb{N}_{k}$	$\mathbb{N}_{k} = \{1, 2, ..., k\}$
card$(A) = k$	cardinality of $A$ is $k$
$aleph_{0}$	cardinality of $\mathbb{N}$
$c$	cardinal number of the continuum