3.1: Direct Proofs
( \newcommand{\kernel}{\mathrm{null}\,}\)
Preview Activity 1 (Definition of Divides, Divisor, Multiple)
In Section 1.2, we studied the concepts of even integers and odd integers. The definition of an even integer was a formalization of our concept of an even integer as being one this is “divisible by 2,” or a “multiple of 2.” We could also say that if “2 divides an integer,” then that integer is an even integer. We will now extend this idea to integers other than 2. Following is a formal definition of what it means to say that a nonzero integer
A nonzero integer
A Note about Notation: Be careful with the notation
A Note about Definitions: Technically, a definition in mathematics should almost always be written using “if and only if.” It is not clear why, but the convention in mathematics is to replace the phrase “if and only if” with “if” or an equivalent. Perhaps this is a bit of laziness or the “if and only if” phrase can be a bit cumbersome. In this text, we will often use the phrase “provided that” instead.
The definition for “divides” can be written in symbolic form using appropriate quantifiers as follows: A nonzero integer
- Use the definition of divides to explain why 4 divides 32 and to explain why 8 divides -96.
- Give several examples of two integers where the first integer does not divide the second integer.
- According to the definition of “divides,” does the integer 10 divide the integer 0? That is, is 10 a divisor of 0? Explain.
- Use the definition of “divides” to complete the following sentence in symbolic form: “The nonzero integer
- Use the definition of “divides” to complete the following sentence without using the symbols for quantifiers: “The nonzero integer
- Give three different examples of three integers where the first integer divides the second integer and the second integer divides the third integer.
As we have seen in Section 1.2, a definition is frequently used when constructing and writing mathematical proofs. Consider the following conjecture:Conjecture: Let
- Explain why the examples you generated in part (6) provide evidence that this conjecture is true.
In Section 1.2, we also learned how to use a know-show table to help organize our thoughts when trying to construct a proof of a statement. If necessary, review the appropriate material in Section 1.2.
- State precisely what we would assume if we were trying to write a proof of the preceding conjecture.
- Use the definition of “divides” to make some conclusions based on your assumptions in part (8).
- State precisely what we would be trying to prove if we were trying to write a proof of the conjecture.
- Use the definition of divides to write an answer to the question, “How can we prove what we stated in part (10)?
Preview Activity 2 (Calendars and Clocks)
This preview activity is intended to help with understanding the concept of congruence, which will be studied at the end of this section.
- Suppose that it is currently Tuesday. (a) What day will it be 3 days from now?
(b) What day will it be 10 days from now?
(c) What day will it be 17 days from now? What day will it be 24 days from now?
(d) Find several other natural numbers
(e) Create a list (in increasing order) of the numbers 3; 10; 17; 24, and the numbers you generated in Part (1d). Pick any two numbers from this list and subtract one from the other. Repeat this several times.
(f) What do the numbers you obtained in Part (1e) have in common? - Suppose that we are using a twelve-hour clock with no distinction between A.M. and P.M. Also, suppose that the current time is 5:00. (a) What time will it be 4 hours from now?
(b) What time will it be 16 hours from now? What time will it be 28 hours from now?
(c) Find several other natural numbers
(d) Create a list (in increasing order) of the numbers 4; 16; 28, and the numbers you generated in Part (2c). Pick any two numbers from this list and subtract one from the other. Repeat this several times.
(e) What do the numbers you obtained in Part (2d) have in common? - This is a continuation of Part (1). Suppose that it is currently Tuesday.
(a) What day was it 4 days ago?
(b) What day was it 11 days ago? What day was it 18 days ago?
(c) Find several other natural numbers
(d) Create a list (in increasing order) consisting of the numbers18; 11; 4, the opposites of the numbers you generated in Part (3c) and the positive numbers in the list from Part (1e). Pick any two num- bers from this list and subtract one from the other. Repeat this several times.
(e) What do the numbers you obtained in Part (3d) have in common?
Some Mathematical Terminology
In Section 1.2, we introduced the idea of a direct proof. Since then, we have used some common terminology in mathematics without much explanation. Before we proceed further, we will discuss some frequently used mathematical terms.
A proof in mathematics is a convincing argument that some mathematical statement is true. A proof should contain enough mathematical detail to be convincing to the person(s) to whom the proof is addressed. In essence, a proof is an argument that communicates a mathematical truth to another person (who has the appropriate mathematical background). A proof must use correct, logical reasoning and be based on previously established results. These previous results can be axioms, definitions, or previously proven theorems. These terms are discussed below.
Surprising to some is the fact that in mathematics, there are always undefined terms. This is because if we tried to define everything, we would end up going in circles. Simply put, we must start somewhere. For example, in Euclidean geometry, the terms “point,” “line,” and “contains” are undefined terms. In this text, we are using our number systems such as the natural numbers and integers as undefined terms. We often assume that these undefined objects satisfy certain properties. These assumed relationships are accepted as true without proof and are called axioms (or postulates). An axiom is a mathematical statement that is accepted without proof. Euclidean geometry starts with undefined terms and a set of postulates and axioms. For example, the following statement is an axiom of Euclidean geometry:
Given any two distinct points, there is exactly one line that contains these two points.
The closure properties of the number systems discussed in Section 1.1 and the properties of the number systems in Table 1.2 on page 18 are being used as axioms in this text.
A definition is simply an agreement as to the meaning of a particular term. For example, in this text, we have defined the terms “even integer” and “odd integer.” Definitions are not made at random, but rather, a definition is usually made because a certain property is observed to occur frequently. As a result, it becomes convenient to give this property its own special name. Definitions that have been made can be used in developing mathematical proofs. In fact, most proofs require the use of some definitions.
In dealing with mathematical statements, we frequently use the terms “conjecture,” “theorem,” “proposition,” “lemma,” and “corollary.” A conjecture is a statement that we believe is plausible. That is, we think it is true, but we have not yet developed a proof that it is true. A theorem is a mathematical statement for which we have a proof. A term that is often considered to be synonymous with “theorem” is proposition.
Often the proof of a theorem can be quite long. In this case, it is often easier to communicate the proof in smaller “pieces.” These supporting pieces are often called lemmas. A lemma is a true mathematical statement that was proven mainly to help in the proof of some theorem. Once a given theorem has been proven, it is often the case that other propositions follow immediately from the fact that the theorem is true. These are called corollaries of the theorem. The term corollary is used to refer to a theorem that is easily proven once some other theorem has been proven.
Constructing Mathematical Proofs
To create a proof of a theorem, we must use correct logical reasoning and mathematical statements that we already accept as true. These statements include axioms, definitions, theorems, lemmas, and corollaries.
In Section 1.2, we introduced the use of a know-show table to help us organize our work when we are attempting to prove a statement. We also introduced some guidelines for writing mathematical proofs once we have created the proof. These guidelines should be reviewed before proceeding.
Please remember that when we start the process of writing a proof, we are essentially “reporting the news.” That is, we have already discovered the proof, and now we need to report it. This reporting often does not describe the process of discovering the news (the investigative portion of the process).
Quite often, the first step is to develop a conjecture. This is often done after working within certain objects for some time. This is what we did in Preview Activity
Conjecture: Let
Before we try to prove a conjecture, we should make sure we have explored some examples. This simply means to construct some specific examples where the integers a, b, and c satisfy the hypothesis of the conjecture in order to see if they also satisfy the conclusion. We did this for this conjecture in Preview Activity
We will now start a know-show table for this conjecture.
| Step | Know | Reason |
| Hypothesis | ||
| ... | ... | ... |
| Step | Show | Reason |
The backward question we ask is, “How can we prove that
We now have to prove that a certain integer
The forward question we ask is, “What can we conclude from the facts that
The key now is to determine how to get from
The last step used the associative property of multiplication. (See Table 1.2 on page 18.) This shows that
| Step | Know | Reason |
| Hypothesis | ||
|
|
Definition of "Divides" | |
| Substitution for |
||
| Associative property of multiplication | ||
| Step |
||
| Definition of "divides" |
Notice the similarities between what we did for this proof and many of the proofs about even and odd integers we constructed in Section 1.2. When we try to prove that a certain object exists, we often use what is called the construction method for a proof. The appearance of an existential quantifier in the show (or backward) portion of the proof is usually the indicator to go to what is known in order to prove the object exists.
We can now report the news by writing a formal proof.
Let
- Proof
-
We assume that
Since
We can now substitute the expression for
Using the associate property for multiplication, we can rearrange the right side of the last equation to obtain
Because both s and t are integers, and since the integers are closed under multiplication, we know that
Writing Guidelines for Equation Numbers
We wrote the proof for Theorem 3.1 according to the guidelines introduced in Section 1.2, but a new element that appeared in this proof was the use of equation numbers. Following are some guidelines that can be used for equation numbers.
If it is necessary to refer to an equation later in a proof, that equation should be centered and displayed. It should then be given it a number. The number for the equation should be written in parentheses on the same line as the equation at the right-hand margin as in shown in the following example.
Since
Later in the proof, there may be a line such as
Then, using the result in equation (1), we obtain . . . .
Notice that we did not number every equation in Theorem 3.1. We should only number those equations we will be referring to later in the proof, and we should only number equations when it is necessary. For example, instead of numbering an equation, it is often better to use a phrase such as, “the previous equation proves that . . . ” or “we can rearrange the terms on the right side of the previous equation.” Also, note that the word “equation” is not capitalized when we are referring to an equation by number. Although it may be appropriate to use a capital “E,” the usual convention in mathematics is not to capitalize.
- Give at least four different examples of integers
- For each example in Part (1), calculate the sum
- Construct a know-show table for the following proposition: For all integers
- Answer
-
Add texts here. Do not delete this text first.
Using Counterexamples
In Section 1.2 and so far in this section, our focus has been on proving statements that involve universal quantifiers. However, another important skill for mathematicians is to be able to recognize when a statement is false and then to be able to prove that it is false. For example, suppose we want to know if the following proposition is true or false.
For each integer
Suppose we start trying to prove this proposition. In the backward process, we would say that in order to prove that 5 divides
For the forward process, we could say that since 5 divides (n^2 - 1), we know that there exists an interger
The problem is that there is no straightforward way to use
| Does 5 divide ( |
Does 5 divide ( |
|||
|---|---|---|---|---|
| 1 | 0 | yes | 0 | yes |
| 2 | 3 | no | 1 | no |
| 3 | 8 | no | 2 | no |
| 4 | 15 | yes | 3 | no |
We can stop exploring examples now since the last row in the table provides an example where the hypothesis is true and the conclusion is false. Recall from Section 2.4 (see page 69) that a counterexample for a statement of the form
When using a counterexample to prove a statement is false, we do not use the term “proof” since we reserve a proof for proving a proposition is true. We could summarize our work as follows:
Conjecture. For each integer
The integer
As a general rule of thumb, anytime we are trying to decide if a proposition is true or false, it is a good idea to try some examples first. The examples that are chosen should be ones in which the hypothesis of the proposition is true. If one of these examples makes the conclusion false, then we have found a counterexample and we know the proposition is false. If all of the examples produce a true conclusion, then we have evidence that the proposition is true and can try to write a proof.
Use a counterexample to prove the following statement is false.
For all integers
- Answer
-
Add texts here. Do not delete this text first.
Congruence
What mathematicians call congruence is a concept used to describe cycles in the world of the integers. For example, the day of the week is a cyclic phenomenon in that the day of the week repeats every seven days. The time of the day is a cyclic phenomenon because it repeats every 12 hours if we use a 12-hour clock or every 24 hours if we use a 24-hour clock. We explored these two cyclic phenomena in Preview Activity
Similar to what we saw in Preview Activity
..., -19, -12, -5, 2, 9, 16, 23, ...
Notice that if we subtract any number in the list above from any other number in that list, we will obtain a multiple of 7. For example,
16 - 2 = 14 = 7
(-5) - (9) = -14 = 7
16 - (-12) = 28 = 7
Using the concept of congruence, we would say that all the numbers in this list are congruent modulo 7, but we first have to define when two numbers are congruent modulo some natural number
Let
Notice that we can use the definition of divides to say that
This means that in order to find integers that are congruent to
... -13, -8, -3, 2, 7, 12, 17,...
We can also write this using set notation and say that
{
- Determine at least eight different integers that are congruent to 5 modulo 8.
- Usesetbuildernotationandtherostermethodtospecifythesetofallintegers
that are congruent to 5 modulo 8.
- Choose two integers that are congruent to 5 modulo 8 and add them. Then repeat this for at least five other pairs of integers that are congruent to 5 modulo 8.
- Explain why all of the sums that were obtained in Part (3) are congruent to 2 modulo 8.
- Answer
-
Add texts here. Do not delete this text first.
We will study the concept of congruence modulo
For all integers
We will use “backward questions” and “forward questions” to help construct a proof for Proposition 3.5. So, we might ask, “How do we prove that (
- Use the definition of divides to determine a way to prove that 8 divides (
We now turn to what we know and ask, "What can we conclude from the assumptions that - Use the definition of divides to make conclusions based on the facts that 8 divides (
- Solve an equation from part (2) for
- Use the results from part (3) to prove that 8 divides (
- Write a proof for Proposition 3.5.
- Answer
-
Add texts here. Do not delete this text first.
Additional Writing Guidelines
We will now be writing many proofs, and it is important to make sure we write according to accepted guidelines so that our proofs may be understood by others. Some writing guidelines were introduced in Chapter 1. The first four writing guidelines given below can be considered general guidelines, and the last three can be considered as technical guidelines specific to writing in mathematics.
- Know your audience. Every writer should have a clear idea of the intended audience for a piece of writing. In that way, the writer can give the right amount of information at the proper level of sophistication to communicate effectively. This is especially true for mathematical writing. For example, if a mathematician is writing a solution to a textbook problem for a solutions manual for instructors, the writing would be brief with many details omitted. However, if the writing was for a students’ solution manual, more details would be included.
- Use complete sentences and proper paragraph structure. Good grammar is an important part of any writing. Therefore, conform to the accepted rules of grammar. Pay careful attention to the structure of sentences. Write proofs using complete sentences but avoid run-on sentences. Also, do not forget punctuation, and always use a spell checker when using a word processor.
- Keep it simple. It is often difficult to understand a mathematical argument no matter how well it is written. Do not let your writing help make it more difficult for the reader. Use simple, declarative sentences and short paragraphs, each with a simple point.
- Write a first draft of your proof and then revise it. Remember that a proof is written so that readers are able to read and understand the reasoning in the proof. Be clear and concise. Include details but do not ramble. Do not be satisfied with the first draft of a proof. Read it over and refine it. Just like any worthwhile activity, learning to write mathematics well takes practice and hard work. This can be frustrating. Everyone can be sure that there will be some proofs that are difficult to construct, but remember that proofs are a very important part of mathematics. So work hard and have fun.
- Do not use
For example, it is very difficult to read (
is much easier to read. - Do not use a mathematical symbol at the beginning of a sentence. For example, we should not write, “Let n be an integer. n is an odd integer provided that . . . .” Many people find this hard to read and often have to re- read it to understand it. It would be better to write, “An integer n is an odd integer provided that . . . .”
- Use English and minimize the use of cumbersome notation. Do not use the special symbols for quantifiers
When it is possible to write
For each real number
Every real number has an additive inverse.
- Prove each of the following statements:
(a) For all integers
(b) For each
(c) For each integer - For each of the following, use a counterexample to prove the statement is false.
(a) For each odd natural number
(b) For each natural number
(c) For all real numbers
(d) For each integer - Determine if each of the following statements is true or false. If a statement is true, then write a formal proof of that statement, and if it is false, then provide a counterexample that shows it is false.
(a) For all integers
(b) For all integers
(c) For all integers
(d) For each integer
(e) For every integer
(f) For every odd integer
(g) For all integer
(h) For all integer - (a) If
(b) Is the following proposition true or false?
For all nonzero integers - Prove the following proposition:
Let
Hint: Use the fact that the only divisors of 1 are 1 and -1. - Determine if each of the following statements is true or false. If a statement is true, then write a formal proof of that statement, and if it is false, then provide a counterexample that shows it is false. (a) For each integer
(a) For each integer
(c) For each integer
(d) For each integer - Let
(a) Prove that if
(b) Prove that if - Let
(a)
(b) - Let
(a)
(b) - Determine if each of the following propositions is true or false. Justify each conclusion.
(a) For all integers
(b) For each integer
(c) For each integer - Let
(a) For every integer
This is called the reflexive property of congruence modulo
(b) For every integer
This is called the symmetric property of congruence modulo
(c) For every integer
This is called the transitive property of congruence modulo - Let
(a) If
(b) If - (a) Let
(b) Prove that if
(c) Prove that if
- Let
We also know that if
Prove that all points on or inside the circle whose equation is - Let
(a) Use implicit differentiation to determine
(b) Let (
(c) Prove that the radius of the circle to the point ( - Determine if each of the following statements is true or false. Provide a counterexample for statements that are false and provide a complete proof for those that are true.
(a) For all real numbers
(b) For all real numbers
(c) For all nonnegative real numbers - Use one of the true in equalities in Exercise(16) to prove the following proposition.
For each real number - (a) State the Pythagorean Theorem for right triangles.
The diagrams in Figure 3.1 will be used for the problems in this exercise.
(b) In the diagram on the left,
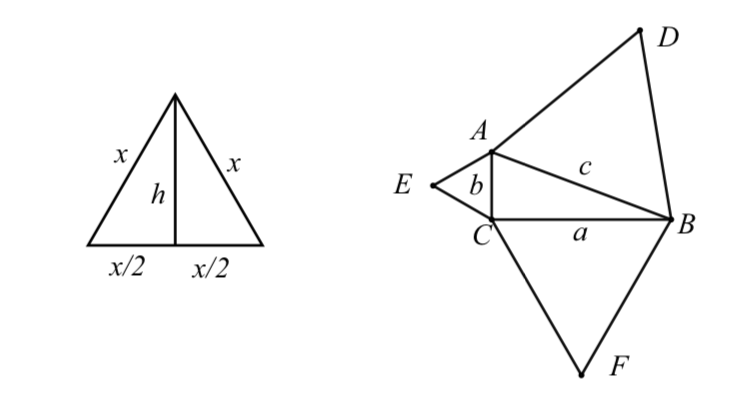
Figure 3.1: Diagrams for Exercise (18)
Pythagorean Theorem to prove that the area of this equilateral triangle is
(c) In the diagram on the right, - Evaluation of proofs
This type of exercise will appear frequently in the book. In each case, there is a proposed proof of a proposition. However, the proposition may be true or may be false.
(a) Proposition. If m is an even integer, then
Proof. We see that
(b) Proposition. For all real numbers
Proof. Since
By combining all terms on the left side of the inequality, we see that
(c) Proposition. For all integers
Proof. We assume that
This means that
(d) Proposition. For all positive integers
This proposition is false as is shown by the following counterexample: If we let
Explorations and Activities - Congruence Modulo 6
(a) Find several integers that are congruent to 5 modulo 6 and then square each of these integers.
(b) For each integer
(c) Based on the work in Part (20b), complete the following conjecture:
For each integer
(d) Complete a know-show table for the conjecture in Part (20c) or write a proof of the conjecture. - Pythagorean Triples. Three natural numbers
(a) Determine all Pythagorean triples consisting of three consecutive natural numbers. (State a theorem and prove it.)
(b) Determine all Pythagorean triples that can be written in the form
- Answer
-
Add texts here. Do not delete this text first.


