8.3: Linear Diophantine Equations

Preview Activity $\PageIndex{1}$: Integer Solutions for Linear Equations in One Variable

1. Does the linear equation $6x = 42$ have a solutions that is an integer? Explain.
2. Does the linear equation $7x = -21$ have a solution that is an integer? Explain.
3. Does the linear equation $4x = 9$ have a solution that is an integer? Explain.
4. Does the linear equation $-3x = 20$ have a solution that is an integer? Explain.
5. Prove the following theorem:

Theorem 8.18

Let $a, b \in \mathbb{Z}$ with $a \ne 0$.

• If $a$ divides $b$, then the equation $ax = b$ has exactly one solution that is an integer.
• If $a$ does not divide $b$, then the equation $ax = b$ has no solution that is an integer.

Preview Activity $\PageIndex{2}$: Linear Equations in Two Variables

1. Find integers $x$ and $y$ so that $2x + 6y = 25$ or explain why it is not possible to find such a pair of integers.
2. Find integers $x$ and $y$ so that $6x - 9y = 100$ or explain why it is not possible to find such a pair of integers.
3. Notice that $x = 2$ and $y = 1$ is a solution of the equation $3x + 5y = 11$, and that $x = 7$ and $y = -2$ is also a solution of the equation $3x + 5y = 11$.

(a) Find two pairs of integers $x$ and $y$ so that $x > 7$ and $3x + 5y = 11$. (Try to keep the integer values of x as small as possible.)
(b) Find two pairs of integers $x$ and $y$ so that $x < 2$ and $3x + 5y = 11$. (Try to keep the integer values of $x$ as close to 2 as possible.)
(c) Determine formulas (one for x and one for y) that will generate pairs of integers $x$ and $y$ so that $3x + 5y = 11$.
Hint: The two formulas can be written in the form $x = 2 + km$ and $y = 1 + kn$, where $k$ is an arbitrary integer and $m$ and $n$ are specific integers.

4. Notice that $x = 4$ and $y = 0$ is a solution of the equation $4x + 6y = 16$, and that $x = 7$ and $y = -2$ is a solution of the equation $4x + 6y = 16$. (a) Find two pairs of integers $x$ and $y$ so that $x > 7$ and $4x + 6y = 16$. (Try to keep the integer values of $x$ as small as possible.)
   (b) Find two pairs of integers $x$ and $y$ so that $x < 4$ and $4x + 6y = 16$. (Try to keep the integer values of $x$ as close to 4 as possible.)
   (c) Determine formulas (one for $x$ and one for $y$) that will generate pairs of integers x and y so that $4x + 6y = 16$.
   Hint: The two formulas can be written in the form $x = 4 + km$ and $y = 0 + kn$, where $k$ is an arbitrary integer and $m$ and $n$ are specific integers.

In the two preview activities, we were interested only in integer solutions for certain equations. In such instances, we give the equation a special name.

Definition: Diophantine equation

An equation whose solutions are required to be integers is called a Diophantine equation.

Diophantine equations are named in honor of the Greek mathematician Diophantus of Alexandria (circa 300 c.e.). Very little is known about Diophantus’ life except that he probably lived in Alexandria in the early part of the fourth centuryc.e. and was probably the first to use letters for unknown quantities in arithmetic problems. His most famous work, Arithmetica, consists of approximately 130 problems and their solutions. Most of these problems involved solutions of equations in various numbers of variables. It is interesting to note that Diophantus did not restrict his solutions to the integers but recognized rational number solutions as well. Today, however, the solutions for a so-called Diophantine equation must be integers.

Definition: linear Diophantine equation in one variable

If $a$ and $b$ are integers with $a \ne 0$, then the equation $ax = b$ is a linear Diophantine equation in one variable.

Theorem 8.18 in Preview Activity $\PageIndex{1}$ provides us with results that allows us to determine which linear diophantine equations in one variable have solutions and which ones do not have a solution.

A linear Diophantine equation in two variables can be defined in a manner similar to the definition for a linear Diophantine equation in one variable.

Definition: linear Diophantine equation in two variables

Let $a$, $b$, and $c$ be integers with $a \ne 0$ and $b \ne 0$. The Diophantine equation $ax + by = c$ is called a linear Diophantine equation in two variables.

The equations that were investigated in Preview Activity $\PageIndex{2}$ were linear Diophantine equations in two variables. The problem of determining all the solutions of a linear Diophantine equation has been completely solved. Before stating the general result, we will provide a few more examples.

Example 8.19: A Linear Diophantine Equation in Two Variables

The following example is similar to the examples studied in Preview Activity $\PageIndex{2}$.

We can use substitution to verify that $x = 2$ and $y = -1$ is a solution of the linear Diophantine equation

$4x + 3y = 5$.

The following table shows other solutions of this Diophantine equation.

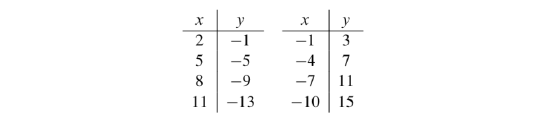
It would be nice to determine the pattern that these solutions exhibit. If we consider the solution $x = 2$ and $y = -1$ to be the “starting point,” then we can see that the other solutions are obtained by adding 3 to $x$ and subtracting 4 from $y$ in the previous solution. So we can write these solutions to the equation as

$x = 2 + 3k$ and $y = -1 - 4k$,

where $k$ is an integer. We can use substitution and algebra to verify that these expressions for $x$ and $y$ give solutions of this equation as follows:

$$\begin{array} {rcl} {4x + 3y} &= & {4(2 + 3k) + 3(-1 - 4k)} \\ {} &= & {(8 + 12k) + (-3 - 12k)} \\ {} &= & {5.} \end{array}$$

We should note that we have not yet proved that these solutions are all of the solutions of the Diophantine equation $4x + 3y = 5$. This will be done later.

If the general form for a linear Diophantine equation is $ax + by = c$, then for this example, $a = 4$ and $b = 3$. Notice that for this equation, we started with one solution and obtained other solutions by adding $b = 3$ to $x$ and subtracting $a = 4$ from $y$ in the previous solution. Also, notice that gcd(3, 4) = 1.

Progress Check 8.20: An Example of a Linear Diophantine Equation

1. Verify that the following table shows some solutions of the linear Diophantine equation $6x + 9y = 12$.
   
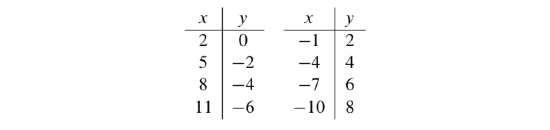
2. Follow the pattern in this table to determine formulas for $x$ and $y$ that will generate integer solutions of the equation $6x + 9y = 12$. Verify that the formulas actually produce solutions for the equation $6x + 9y = 12$.

Answer

Add texts here. Do not delete this text first.

Progress Check 8.21: Revisiting Preview Activity $\PageIndex{2}$

Do the solutions for the linear Diophantine equations in Preview Activity $\PageIndex{2}$ show the same type of pattern as the solutions for the linear Diophantine equations in Example 8.19 and Progress Check 8.20? Explain.

Answer

Add texts here. Do not delete this text first.

The solutions for the linear Diophantine equations in Preview Activity $\PageIndex{2}$, Example 8.19, and Progress Check 8.20 provide examples for the second part of Theorem 8.22.

Theorem 8.22

Let $a$, $b$ and $c$ be integers with $a \ne 0$ and $b \ne 0$, and let $d = \text{gcd}(a, b)$.

1. If $d$ does not divide $c$, then the linear Diophantine equation $ax + by = c$ has no solution.
2. If $d$ divides $c$, then the linear Diophantine equation $ax + by = c$ has infinitely many solutions. In addition, if ($x_0$, $y_0$) is a particular solution of this equation, then all the solutions of this equation can be written in the form
   $$x = x_0 + \dfrac{b}{d} k\ \ \ \ \ \ \ \ \text{and}\ \ \ \ \ \ \ \ y = y_0 - \dfrac{a}{d} k,$$
   for some integer $k$.

Proof

The proof of Part (1) is Exercise (1). For Part (2), we let $a$, $b$, and $c$ be integers with $a \ne 0$ and $b \ne 0$, and let $d = \text{gcd}(a, b)$. We also assume that $d\ |\ c$. Since $d = \text{gcd}(a, b)$, Theorem 8.8 tells us that $d$ is a linear combination of $a$ and $b$. So there exist integers $s$ and $t$ such that

$$d = as + bt.$$

Since $d\ |\ c$, there exists an integer $m$ such that $c = dm$. We can now multiply both sides of equation (8.3.3) by m and obtain

$$\begin{array} {rcl} {dm} &= & {(as + bt)m} \\ {c} &= & {a(sm) + b(tm).} \end{array}$$

This means that $x = sm$, $y = tm$ is a solution of $ax + by = c$, and we have proved that the Diophantine equation $ax + by = c$ has at least one solution.

Now let $x = x_0, y = y_0$ be any particular solution of $ax + by = c$, let $k \in \mathbb{Z}$, and let

$$x = x_0 + \dfrac{b}{d} k\ \ \ \ \ \ \ \ y = y_0 - \dfrac{a}{d} k.$$

We now verify that for each $k \in \mathbb{Z}$, the equations in (8.3.4) produce a solution of $ax + by = c$.

$$\begin{array} {rcl} {ax + by} &= & {a(x_0 + \dfrac{b}{d} k) + b(y_0 - \dfrac{a}{d} k)} \\ {} &= & {ax_0 + \dfrac{ab}{d} k + by_0 - \dfrac{ab}{d} k} \\ {} &= & {ax_0 + by_0} \\ {} &= & {c.} \end{array}$$

This proves that the Diophantine equation $ax + by = c$ has infinitely many solutions.

We now show that every solution of this equation can be written in the form described in (8.3.4). So suppose that $x$ and $y$ are integers such that $ax + by = c$. Then

$(ax + by) - (ax_0 + by_0) = c - c = 0,$

and this equation can be rewritten in the following form:

$$a(x - x_0) = b(y_0 - y).$$

Dividing both sides of this equation by $d$, we obtain

$(\dfrac{a}{d}) (x - x_0) = (\dfrac{b}{d}) (y_0 - y).$

This implies that

$\dfrac{a}{d}$ divides $(\dfrac{b}{d}) (y_0 - y).$

However, by Exercise (7) in Section 8.2, $text{gcd}(\dfrac{a}{d}, \dfrac{b}{d}) = 1$, and so by Theorem 8.12, we can conclude that $\dfrac{a}{d}$ divides $y_0 - y$. This means that there exists an integer $k$ such that $y_0 - y = \dfrac{a}{d} k$, and solving for $y$ gives

$y = y_0 - \dfrac{a}{d} k.$

Substituting this value for $y$ in equation (8.3.5) and solving for $x$ yields

$x = x_0 + \dfrac{b}{d}) k.$

This proves that every solution of the Diophantine equation $ax + by = c$ can be written in the form prescribed in (8.3.4).

The proof of the following corollary to Theorem 8.22 is Exercise (2)

Theorem $\PageIndex{1}$

Let $a$, $b$, and $c$ be integers with $a \ne 0$ and $b \ne 0$.If $a$ and $b$ are relatively prime, then the linear Diophantine equation $ax + by = c$ has infinitely many solutions. In addition, if $x_0$, $y_0$ is a particular solution of this equation, then all the solutions of the equation are given by

$x = x_0 + bk$ $y = y_0 - ak$

where $k \in \mathbb{Z}$

Progress Check 8.24 (Linear Diophantine Equations)

1. Use the Euclidean Algorithm to verify that gcd.63; 336/ D 21. What conclusion can be made about linear Diophantine equation $63x + 336y = 40$ using Theorem 8.22? If this Diophantine equation has solutions, write formulas that will generate the solutions.
2. Use the Euclidean Algorithm to verify that gcd.144; 225/ D 9. What conclusion can be made about linear Diophantine equation $144x + 225y = 27$ using Theorem 8.22? If this Diophantine equation has solutions, write formulas that will generate the solutions.

Answer

Add texts here. Do not delete this text first.

Exercises 8.3

1. Prove Part (1) of Theorem 8.22:

   Let $a$, $b$, and $c$ be integers with $a \ne 0$ and $b \ne 0$, and let $d = \text{gcd}(a, b)$. If $d$ does not divide $c$, then the linear Diophantine equation $ax + by = c$ has no solution.

2. Prove Corollary 8.23.

   Let $a$, $b$, and $c$ be integers with $a \ne 0$ and $b \ne 0$. If $a$ and $b$ are relatively prime, then the linear Diophantine equation $ax + by = c$ has infinitely many solutions. In addition, if ($x_0, y_0$) is a particular solution of this equation, then all the solutions of the equation are given by
   $$x = x_0 + bk\ \ \ \ \ \ \ y = y_0 - ak,$$
   where $k \in \mathbb{Z}$.

3. Determine all solutions of the following linear Diophantine equations.
   
   (a) $9x + 14y = 1$
   (b) $18x + 22y = 4$
   (c) $48x - 18y = 15$
   (d) $12x + 9y = 6$
   (e) $200x + 49y = 10$
   (f) $200x + 54y = 21$
   (g) $10x - 7y = 31$
   (h) $12x + 18y = 6$
4. A certain rare artifact is supposed to weigh exactly 25 grams. Suppose that you have an accurate balance scale and 500 each of 27 gram weights and 50 gram weights. Explain how to use Theorem 8.22 to devise a plan to check the weight of this artifact.

   Hint: Notice that gcd(50, 27) = 1. Start by writing 1 as a linear combination of 50 and 27.

5. On the night of a certain banquet, a caterer offered the choice of two dinners, a steak dinner for $25 and a vegetarian dinner for $16. At the end of the evening, the caterer presented the host with a bill (before tax and tips) for $1461. What is the minimum number of people who could have attended the banquet? What is the maximum number of people who could have attended the banquet?
6. The goal of this exercise is to determine all (integer) solutions of the linear Diophantine equation in three variables $12x_1 + 9x_2 + 16x_3 = 20.$
   
   (a) First, notice that gcd(12, 9) = 3. Determine formulas that will generate all solutions for the linear Diophantine equation $3y + 16x_3 = 20$.
   (b) Explain why the solutions (for $x_1$ and $x_2$) of the Diophantine equation $12x_1 + 9x_2 = 3y$ can be used to geneate solutions for $12x_1 + 9x_2 + 16x_3 = 20$.
   (c) Use the general value for y from Exercise (6a) to determine the solutions of $12x_1 + 9x_2 = 3y$
   (d) Use the results from Exercises (6a) and (6c) to determine formulas that will generate all solutions for the Diophantine equation $12x_1 + 9x_2 + 16x_3 = 20$.
   Note: These formulas will involve two arbitrary integer parameters. Substitute specific values for these integers and then check the resulting solution in the original equation. Repeat this at least three times.
   (e) Check the general solution for $12x_1 + 9x_2 + 16x_3 = 20$ from Exercise (6d).
7. Use the method suggested in Exercise (6) to determine formulas that will generate all solutions of the Diophantine equation $8x_1 + 4x_2 - 6x_3 = 6$. Check the general solution.
8. Explain why the Diophantine equation $24x_1 - 18x_2 + 60x_3 = 21$ has no solution.
9. The purpose of this exercise will be to prove that the nonlinear Diophantine equation $3x^2 - y^2 = -2$ has no solution.
   
   (a) Explain why if there is a solution of the Diophantine equation $3x^2 - y^2 = -2$, then that solution must also be a solution of the congruence $3x^2 - y^2 \equiv -2$ (mod 3).
   (b) If there is a solution to the congruence $3x^2 - y^2 \equiv -2$ (mod 3), explain why there then must be an integer $y$ such that $y^2 \equiv 2$ (mod 3).
   (c) Use a proof by contradiction to prove that the Diophantine equation $3x^2 - y^2 = -2$ has no solution.
10. Use the method suggested in Exercise (9) to prove that the Diophantine equation $7x^2 + 2 = y^3$ has no solution.
    
    Explorations and Activities
11. Linear Congruences in One Variable. Let $n$ be a natural number and let $a, b \in \mathbb{Z}$ with $a \ne 0$. A congruence of the form $ax \equiv b$ (mod $n$) is called a linear congruence in one variable. This is called a linear congruence since the variable $x$ occurs to the first power.

    A solution of a linear congruence in one variable is defined similarly to the solution of an equation. A solution is an integer that makes the resulting congruence true when the integer is substituted for the variable $x$. For example,
    
    $\bullet$ The integer $x = 3$ is a solution for the congruence $2x \equiv 1$ (mod 5) since $2 \cdot 3 \equiv 1$ (mod 5) is a true congruence.
    $\bullet$ The integer $x = 7$ is a solution for the congruence $3x \equiv 1$ (mod 6) since $3 \cdot 7 \equiv 1$ (mod 6) is not a true congruence.
    
    (a) Verify that $x = 2$ and $x = 5$ are the only solutions the linear congruence $4x \equiv 2$ (mod 6) with $0 \le x < 6$.
    (b) Show that the linear congruence $4x \equiv 3$ (mod 6) has no solutions with $0 \le x < 6$.
    (c) Determine all solutions of the linear congruence $3x \equiv 7$ (mod 8) with $0 \le x < 8$.
    
    The following parts of this activity show that we can use the results of Theorem 8.22 to help find all solutions of the linear congruence $6x \equiv 4$ (mod 8).
    
    (d) Verify that $x = 2$ and $x = 5$ are the only solutions the linear congruence $6x \equiv 4$ (mod 8) with $0 \le x < 8$.
    (e) Use the definition of “congruence” to rewrite the congruence $6x \equiv 4$ (mod 8) in terms of "divides".
    (f) Use the definition of “divides” to rewrite the result in part (11e) in the form of an equation. (An existential quantifier must be used.)
    (g) Use the results of parts (11d) and (11f) to write an equation that will generate all the solutions of the linear congruence $6x \equiv 4$ (mod 8).
    Hint: Use Theorem 8.22. This can be used to generate solutions for $x$ and the variable introduced in part (11f). In this case, we are interested only in the solutions for $x$.
    
    Now let $n$ be a natural number and let $a, c \in \mathbb{Z}$ with $a \ne 0$. A general linear congruence of the form $ax \equiv c$ (mod $n$) can be handled in the same way that we handled in $6x \equiv 4$ (mod 8).
    
    (h) Use the definition of “congruence” to rewrite $ax \equiv c$ (mod $n$) in terms of “divides.”
    (i) Use the definition of “divides” to rewrite the result in part (11h) in the form of an equation. (An existential quantifier must be used.)
    (j) Let $d = \text{gcd}(a, n)$. State and prove a theorem about the solutions of the linear congruence $ax \equiv c$ (mod $n$) in the case where $d$ does not divide $c$.
    Hint: Use Theorem 8.22.
    (k) Let $d = \text{gcd}(a, n)$. State and prove a theorem about the solutions of the linear congruence $ax \equiv c$ (mod $n$) in the case where $d$ divides $c$.

Answer

Add texts here. Do not delete this text first.