1.2: Definitions - Prime Numbers
- Page ID
- 19361
You may have noticed that in Section 1.1 an awful lot of emphasis was placed on whether we had good, precise definitions for things. Indeed, more than once apologies were made for giving imprecise or intuitive definitions. This is because, in Mathematics, definitions are our lifeblood. More than in any other human endeavor, Mathematicians strive for precision. This precision comes with a cost – Mathematics can deal with only the very simplest of phenomena1. To laypeople who think of math as being a horribly difficult subject, that last sentence will certainly sound odd, but most professional Mathematicians will be nodding their heads at this point. Hard questions are more properly dealt with by Philosophers than by Mathematicians. Does a cat have a soul? Impossible to say, because neither of the nouns in that question can be defined with any precision. Is the square root of \(2\) a rational number? Absolutely not! The reason for the certainty we feel in answering this second question is that we know precisely what is meant by the phrases “square root of \(2\)” and “rational number.”
We often need to first approach a topic by thinking visually or intuitively, but when it comes to proving our assertions, nothing beats the power of having the “right” definitions around. It may be surprising to learn that the “right” definition often evolves over the years. This happens for the simple reason that some definitions lend themselves more easily to proving assertions. In fact, it is often the case that definitions are inspired by attempts to prove something that fail. In the midst of such a failure, it isn’t uncommon for a Mathematician to bemoan “If only the definition of (fill in the blank) were . . . ”, then to realize that it is possible to use that definition or a modification of it. But! When there are several definitions for the same idea they had better agree with one another!
Consider the definition of a prime number.
A prime number is a positive integer, greater than \(1\), whose only factors are \(1\) and itself.
You probably first heard this definition in Middle School, if not earlier. It is a perfectly valid definition of what it means for an integer to be prime. In more advanced mathematics, it was found that it was necessary to define a notion of primality for objects other than integers. It turns out that the following statement is essentially equivalent to the definition of “prime” we’ve just given (when dealing with integers), but that it can be applied in more general settings.
A prime is a quantity \(p\) such that whenever \(p\) is a factor of some product \(ab\), then either \(p\) is a factor of \(a\) or \(p\) is a factor of \(b\|).
The number \(1\) is not considered to be a prime. Does \(1\) satisfy the above definition?
If you go on to study Number Theory or Abstract Algebra you’ll see how the alternate definition we’ve given needs to be tweaked so that (for example) \(1\) wouldn’t get counted as a prime. The fix isn’t hugely complicated (but it is a little complicated) and is a bit beyond our scope right now. . .
Often, it is the case that we can formulate many equivalent definitions for some concept. When this happens you may run across the abbreviation TFAE, which stands for “The following are equivalent.” A TFAE proof consists of showing that a host of different statements actually define the same concept.
Since we have been discussing primes in this section (mainly as an example of a concept with more than one equivalent definition), this seems like a reasonable time to make some explorations relative to prime numbers. We’ll begin in the third century B.C. Eratosthenes of Cyrene was a Greek Mathematician and Astronomer who is remembered to this day for his many accomplishments. He was a librarian at the great library of Alexandria. He made measurements of the Earth’s circumference and the distances of the Sun and Moon that were remarkably accurate, but probably his most remembered achievement is the “sieve” method for finding primes. Indeed, the sieve of Eratosthenes is still of importance in mathematical research. Basically, the sieve method consists of creating a very long list of natural numbers and then crossing off all the numbers that aren’t primes (a positive integer that isn’t \(1\), and isn’t a prime is called composite). This process is carried out in stages. First, we circle \(2\) and then cross off every number that has \(2\) as a factor – thus we’ve identified \(2\) as the first prime number and eliminated a whole bunch of numbers that aren’t prime. The first number that hasn’t been eliminated at this stage is \(3\), we circle it (indicating that \(3\) is the second prime number) and then cross off every number that has \(3\) as a factor. Note that some numbers (for example, \(6\) and \(12\)) will have been crossed off more than once! In the third stage of the sieve process, we circle \(5\), which is the smallest number that hasn’t yet been crossed off, and then cross off all multiples of \(5\). The first three stages in the sieve method are shown in Figure \(1.2.1\).
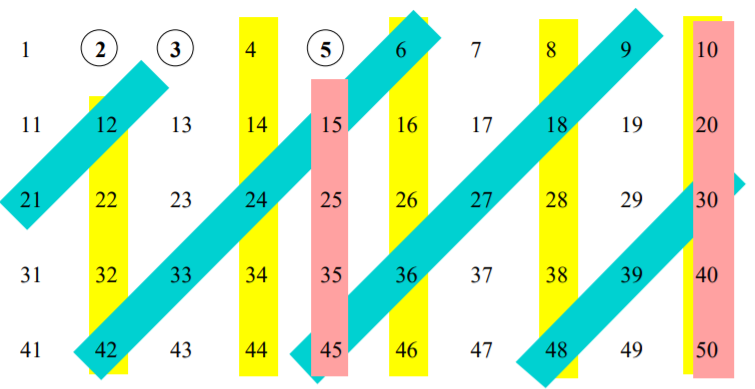
It is interesting to note that the sieve gives us a means of finding all the primes up to \(p^2\) by using the primes up to (but not including) \(p\). For example, to find all the primes less than \(13^2 = 169\), we need only use \(2\), \(3\), \(5\), \(7\) and \(11\) in the sieve.
Despite the fact that one can find primes using this simple mechanical method, the way that prime numbers are distributed amongst the integers is very erratic. Nearly any statement that purports to show some regularity in the distribution of the primes will turn out to be false. Here are two such false conjectures regarding prime numbers.
Whenever \(p\) is a prime number, \(2^p − 1\) is also a prime.
The polynomial \(x^2 − 31x + 257\) evaluates to a prime number whenever \(x\) is a natural number.
In the exercises for this section, you will be asked to explore these statements further.
Prime numbers act as multiplicative building blocks for the rest of the integers. When we disassemble an integer into its building blocks we are finding the prime factorization of that number. Prime factorizations are unique. That is, a number is either prime or it has prime factors (possibly raised to various powers) that are uniquely determined – except that they may be re-ordered.
Below is a table that contains all the primes that are less than \(5000\). Study this table and discover the secret of its compactness!
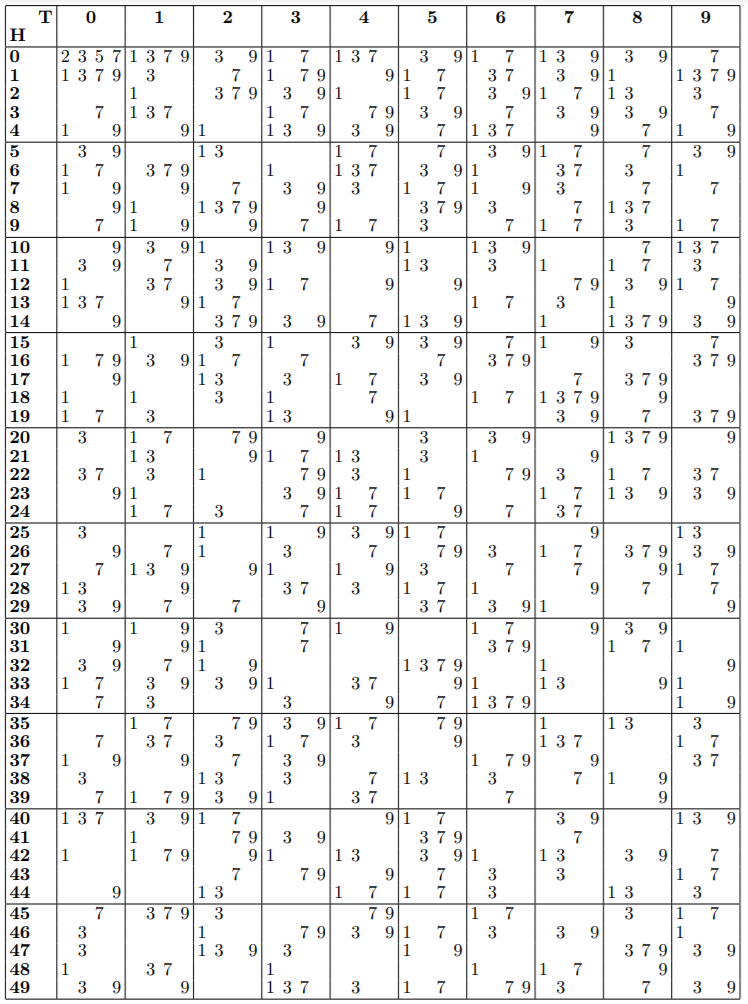
Exercises
Find the prime factorizations of the following integers.
- 105
- 414
- 168
- 1612
- 9177
Use the sieve of Eratosthenes to find all prime numbers up to \(100\).
\[ \begin{array} a1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20\\ 21 & 22 & 23 & 24 & 25 & 26 & 27 & 28 & 29 & 30\\ 31 & 32 & 33 & 34 & 35 & 36 & 37 & 38 & 39 & 40 \\ 41 & 42 & 43 & 44 & 45 & 46 & 47 & 48 & 49 & 50 \\ 51 & 52 & 53 & 54 & 55 & 56 & 57 & 58 & 59 & 60 \\ 61 & 62 & 63 & 64 & 65 & 66 & 67 & 68 & 69 & 70 \\ 71 & 72 & 73 & 74 & 75 & 76 & 77 & 78 & 79 & 80 \\ 81 & 82 & 83 & 84 & 85 & 86 & 87 & 88 & 89 & 90 \\ 91 & 92 & 93 & 94 & 95 & 96 & 97 & 98 & 99 & 100 \\ \end{array} \]
What would be the largest prime one would sieve with in order to find all primes up to 400?
Characterize the prime factorizations of numbers that are perfect squares.
Complete the following table which is related to Conjecture \(1.2.1\).
| \(p\) | \(2^p - 1\) | prime? | factors |
| \(2\) | \(3\) | yes | \(1\) and \(3\) |
| \(3\) | \(7\) | yes | \(1\) and \(7\) |
| \(5\) | \(31\) | yes | |
| \(7\) | \(127\) | ||
| \(11\) |
Find a counterexample for Conjecture \(1.2.2\)
Use the second definition of “prime” to see that \(6\) is not a prime. In other words, find two numbers (the a and b that appear in the definition) such that \(6\) is not a factor of either, but is a factor of their product.
Use the second definition of “prime” to show that \(35\) is not a prime.
A famous conjecture that is thought to be true (but for which no proof is known) is the Twin Prime conjecture. A pair of primes is said to be twin if they differ by \(2\). For example, \(11\) and \(13\) are twin primes, as are \(431\) and \(433\). The Twin Prime conjecture states that there are an infinite number of such twins. Try to come up with an argument as to why \(3\), \(5\) and \(7\) are the only prime triplets.
Another famous conjecture, also thought to be true – but as yet unproved, is Goldbach’s conjecture. Goldbach’s conjecture states that every even number greater than \(4\) is the sum of two odd primes. There is a function \(g(n)\), known as the Goldbach function, defined on the positive integers, that gives the number of different ways to write a given number as the sum of two odd primes. For example, \(g(10) = 2\) since \(10 = 5 + 5 = 7 + 3\). Thus another version of Goldbach’s conjecture is that \(g(n)\) is positive whenever n is an even number greater than \(4\).
Graph \(g(n)\) for \(6 ≤ n ≤ 20\).


