2.1: Predicates and Logical Connectives
- Page ID
- 19367
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In every branch of Mathematics there are special, atomic, notions that defy precise definition. In Geometry, for example, the atomic notions are points, lines and their incidence. Euclid defines a point as “that which has no part” – people can argue (and have argued) incessantly over what exactly is meant by this. Is it essentially saying that anything without volume, area or length of some sort is a point? In modern times it has been recognized that any formal system of argumentation has to have such elemental, undefined, concepts – and that Euclid’s apparent lapse in precision comes from an attempt to hide this basic fact. The notion of “point” can’t really be defined. All we can do is point (no joke intended) at a variety of points and hope that our audience will absorb the same concept of point that we hold via the process of induction1.
The atomic concepts in Set Theory are “set”, “element” and “membership”. The atomic concepts in Logic are “true”, “false”, “sentence” and “statement”.
Regarding true and false, we hope there is no uncertainty as to their meanings. Sentence also has a well-understood meaning that most will agree on – a syntactically correct ordered collection of words such as “Johnny was a football player.” or “Red is a color.” or “This is a sentence which does not refer to itself.” A statement is a sentence which is either true or false. In other words, a statement is a sentence whose truth value is definite, in more other words, it is always possible to decide – one way or the other – whether a statement is true or false.2 The first example of a sentence given above (“Johnny was a football player”) is not a statement – the problem is that it is ambiguous unless we know who Johnny is. If it had said “Johnny Unitas was a football player.” then it would have been a statement. If it had said “Johnny Appleseed was a football player.” it would also have been a statement, just not a true one.
Ambiguity is only one reason that a sentence may not be a statement. As we consider more complex sentences, it may be the case that the truth value of a given sentence simply cannot be decided. One of the most celebrated mathematical results of the \(20^{\text{th}}\) century is Kurt Gödel’s “Incompleteness Theorem.” An important aspect of this theory is the proof that in any axiomatic system of mathematical thought there must be undecidable sentences – statements which can neither be proved nor disproved from the axioms3. Simple sentences (e.g. those of the form subject-verb-object) have little chance of being undecidable for this reason, so we will next look at ways of building more complex sentences from simple components.
Let’s start with an example. Suppose I come up to you in some windowless room and make the statement: “The sun is shining but it’s raining!” You decide to investigate my claim and determine its veracity. Upon reaching a room that has a view of the exterior there are four possible combinations of sunniness and/or precipitation that you may find. That is, the atomic predicates “The sun is shining” and “It is raining” can each be true or false independently of one another. In the following table we introduce a convention used throughout the remainder of this book – that true is indicated with a capital letter \(\text{T}\) and false is indicated with the Greek letter \(\phi\) (which is basically a Greek \(\text{F}\), and is a lot harder to mistake for a \(\text{T}\) than an \(\text{F}\) is.)
| The Sun is Shining | It is Raining |
|---|---|
| \(\text{T}\) | \(\text{T}\) |
| \(\text{T}\) | \(\phi\) |
| \(\phi\) | \(\text{T}\) |
| \(\phi\) | \(\phi\) |
Each row of the above table represents a possible state of the outside world. Suppose you observe the conditions given in the last row, namely that it is neither sunny, nor is it raining – you would certainly conclude that I am not to be trusted. I.e. my statement, the compounding of “The sun is shining” and “It is raining” (with the word “but” in between as a connector) is false. If you think about it a bit, you’ll agree that this so-called compound sentence is true only in the case that both of its component pieces are true. This underscores an amusing linguistic point: “but” and “and” have exactly the same meaning! More precisely, they denote the same thing, they have subtly different connotations however – “but” indicates that both of the statements it connects are true and that the speaker is surprised by this state of affairs.
In Mathematics we distinguish two main connectives for hooking-up simple sentences into compound ones. The conjunction of two sentences is the compound sentence made by sticking the word “and” between them. The disjunction of two sentences is formed by placing an “or” between them. Conjunctions are true only when both components are true. Disjunctions are false only when both components are false.
As usual, mathematicians have developed an incredibly terse, compact notation for these ideas.4 First, we represent an entire sentence by a single letter – traditionally, a capital letter. This is called a predicate variable. For example, following the example above, we could denote the sentence “The sun is shining” by the letter \(\text{S}\). Similarly, we could make the assignment \(\text{R} =\) “It is raining.” The conjunction and disjunction of these sentences can then be represented using the symbols \(S ∧ R and \(S ∨ R\), respectively. As a mnemonic, note that the connective in \(S ∧ R\) looks very much like the capital letter \(\text{A}\) (as in And).
To display, very succinctly, the effect of these two connectives we can use so-called truth tables. In a truth table, we list all possible truth values of the predicate variables and then enumerate the truth values of some compound sentence. For the conjunction and disjunction connectors we have (respectively):
| \(A\) | \(B\) | \(A ∧ B\) |
|---|---|---|
| \(\text{T}\) | \(\text{T}\) | \(\text{T}\) |
| \(\text{T}\) | \(\phi\) | \(\phi\) |
| \(\phi\) | \(\text{T}\) | \(\phi\) |
| \(\phi\) | \(\phi\) | \(\phi\) |
and
| \(A\) | \(B\) | \(A ∨ B\) |
|---|---|---|
| \(\text{T}\) | \(\text{T}\) | \(\text{T}\) |
| \(\text{T}\) | \(\phi\) | \(\text{T}\) |
| \(\phi\) | \(\text{T}\) | \(\text{T}\) |
| \(\phi\) | \(\phi\) | \(\phi\) |
In addition to these connectors we need a modifier (called negation) that acts on individual sentences. The negation of a sentence \(A\) is denoted by \(¬A\), and its truth value is exactly the opposite of \(A\)’s truth value. The negation of a sentence is also known as the denial of a sentence. A truth table for the negation operator is somewhat trivial but we include it here for completeness.
| \(A\) | \(¬A\) |
|---|---|
| \(\text{T}\) | \(\phi\) |
| \(\phi\) | \(\text{T}\) |
These three simple tools (and, or & not) are sufficient to create extraordinarily complex sentences out of basic components. The way these pieces interrelate is a bit reminiscent of algebra, in fact, the study of these logical operators (or any operators that act like them) is called Boolean Algebra5. There are distinct differences between Boolean and ordinary algebra however. In regular algebra we have the binary connectors \(+\) (plus) and \(·\) (times), and the unary negation operator \(−\), these are certainly analogous to \(∧\), \(∨\) & \(¬\), but there are certain consequences of the fact that multiplication is effectively repeated addition that simply don’t hold for the Boolean operators. For example, there is a well-defined precedence between \(·\) and \(+\). In parsing the expression \(4 · 5 + 3\) we all know that the multiplication is to be done first. There is no such rule governing order of operations between \(∧\) and \(∨\), so an expression like \(A ∧ B ∨ C\) is simply ambiguous – it must have parentheses inserted in order to show the order, either \((A∧B)∨C\) or \(A∧(B∨C)\). Another distinction between ordinary and Boolean algebra is exponentiation. If there were exponents in Boolean algebra, we’d need two different kinds – one for repeated conjunction and another for repeated disjunction.
Why is it that there is no such thing as exponentiation in the algebra of Logic?
While there are many differences between Boolean algebra and the usual, garden-variety algebra, there are also many similarities. For instance, the associative, commutative and distributive laws of Algebra all have versions that work in the Boolean case.
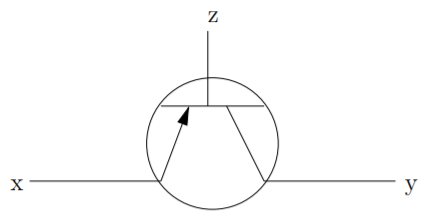
A very handy way of visualizing Boolean expressions is given by digital logic circuit diagrams. To discuss these diagrams we must make a brief digression into Electronics. One of the most basic components inside an electronic device is a transistor, this is a component that acts like a switch for electricity, but the switch itself is controlled by electricity. In Figure \(2.1.1\) we see the usual schematic representation of a transistor. If voltage is applied to the wire labeled \(\text{z}\), the transistor becomes conductive, and current may flow from \(\text{x}\) to \(\text{y}\).
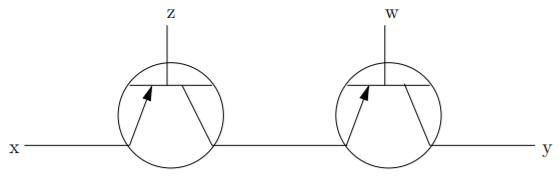
Suppose that two transistors are connected as in Figure \(2.1.2\) (this is called a series connection). In order for current to flow from \(\text{x}\) to \(\text{y}\) we must have voltage applied to both the wires labeled \(\text{z}\) and \(\text{w}\). In other words, this circuit effectively creates the and operation – assuming voltage is always applied to \(\text{x}\), if \(z\) and \(\text{w}\) are energized then the output at \(\text{y}\) will be energized.
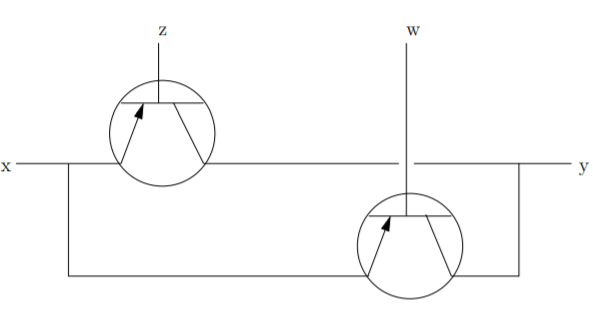
When two transistors are connected in parallel (this is illustrated in Figure \(2.1.3\)) current can flow from \(\text{x}\) to \(\text{y}\) when either (or both) of the wires at \(\text{z}\) and \(\text{w}\) have voltage applied. This brings up a point which is confusing for some: in common speech the use of the word “or” often has the sense known as exclusive or (a.k.a. xor), when we say “\(\text{X}\) or \(\text{Y}\)” we mean “Either X or Y, but not both.” In Electronics and Mathematics, or always has the non-exclusive (better known as inclusive) sense.
As a sort of graphical shorthand, electronics engineers use the symbols below to indicate and-gates, or-gates & not-gates (better known as negators).
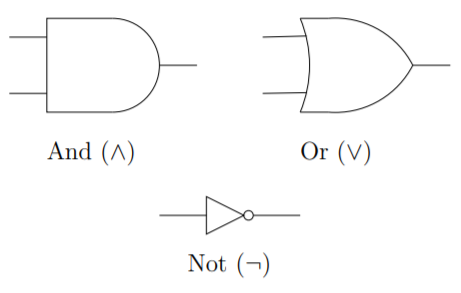
An and-gate has two transistors inside it that are wired in series – if both the inputs are energized the output will be too. An or-gate has two transistors in parallel inside it. Not-gates involve magic – when their input is not on, their output is and vice versa.
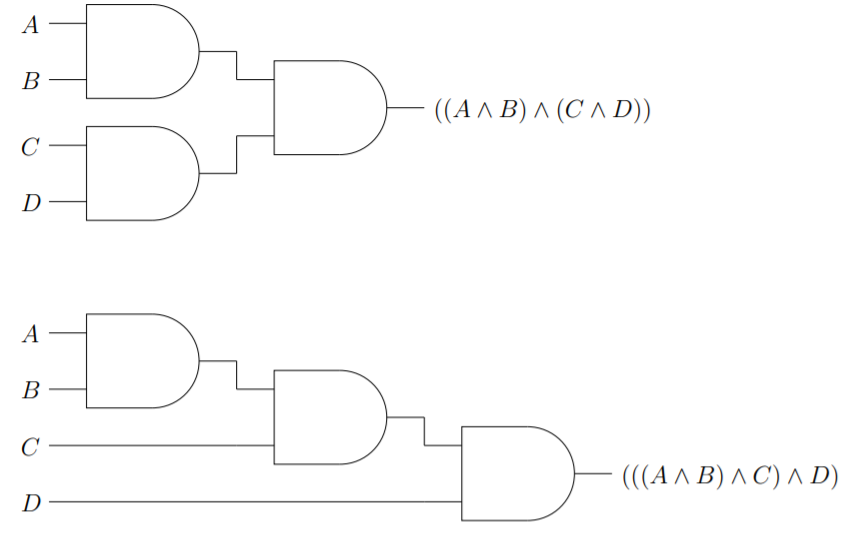
Using this graphical “language” one can make schematic representations of logical expressions. Some find that tracing such diagrams makes understanding the structure of a Boolean expression easier. For example, in Figure \(2.1.4\) we illustrate \(2\) of the possible ways that the conjunction of four predicate variables can be parenthesized. In fact, when a multitude of predicates are joined by the same connective, the way in which the expression is parenthesized is unimportant, thus one often sees a further shorthand — gates with more than \(2\) inputs.
A common task for an electronics designer is to come up with a digital logic circuit having a prescribed input/output table. Note that an input/output table for a logic circuit is entirely analogous with a truth table for a compound sentence in Logic — except that we use \(0\)’s and \(1\)’s rather than \(\text{T}\)’s and \(\phi\)’s.
Suppose that we wanted to design a circuit that would have the following input/output table.
| \(x\) | \(y\) | \(z\) | \(\text{out}\) |
|---|---|---|---|
| \(0\) | \(0\) | \(0\) | \(0\) |
| \(0\) | \(0\) | \(1\) | \(0\) |
| \(0\) | \(1\) | \(0\) | \(0\) |
| \(0\) | \(1\) | \(1\) | \(1\) |
| \(1\) | \(0\) | \(0\) | \(0\) |
| \(1\) | \(0\) | \(1\) | \(0\) |
| \(1\) | \(1\) | \(0\) | \(1\) |
| \(1\) | \(1\) | \(1\) | \(1\) |
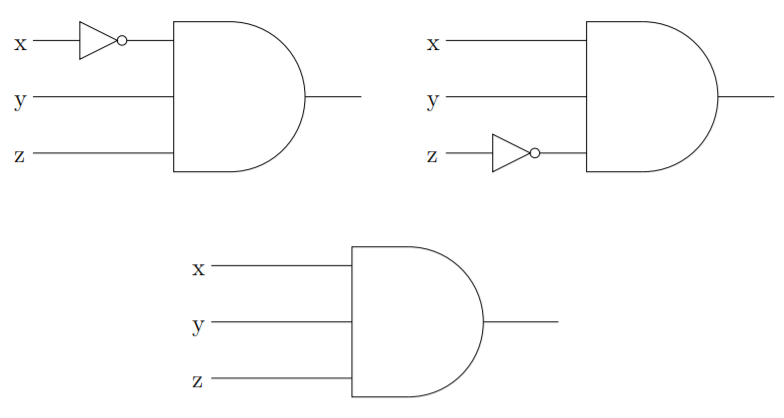
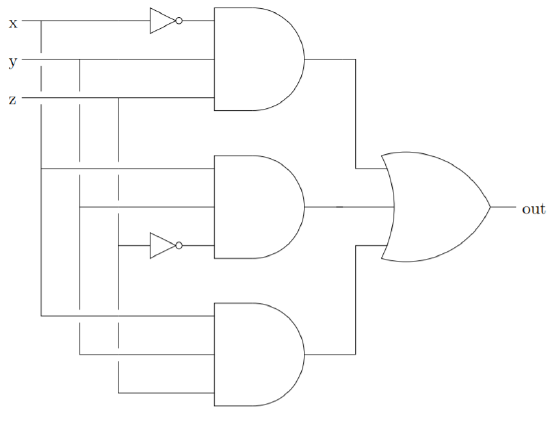
A systematic method for accomplishing such a design task involves a notion called disjunctive normal form. A Boolean expression is in disjunctive normal form if it consists of the disjunction of one or more statements, each of which consists entirely of conjunctions of predicate variables and/or their negations. In other words, the or of a bunch of ands. In terms of digital logic circuits, the ands we’re talking about are called recognizers. For example, the following \(3\)-input and-gates recognize the input states in the \(4^{\text{th}}\), \(7^{\text{th}}\) and \(8^{\text{th}}\) rows of the i/o table above. (These are the rows where the output is supposed to be \(1\).)
In Figure \(2.1.5\) we illustrate how to create a circuit whose i/o table is as above using these recognizers.
Exercises
Design a digital logic circuit (using and, or & not gates) that implements an exclusive or
Consider the sentence “This is a sentence which does not refer to itself.” which was given in the beginning of this chapter as an example. Is this sentence a statement? If so, what is its truth value?
Consider the sentence “This sentence is false.” Is this sentence a statement?
Complete truth tables for each of the sentences \((A∧B)∨C\) and \(A∧(B∨ C)\). Does it seem that these sentences have the same logical content?
There are two other logical connectives that are used somewhat less commonly than \(∨\) and \(∧\). These are the Scheffer stroke and the Peirce arrow – written \(|\) and \(↓\), respectively — they are also known as NAND and NOR.
The truth tables for these connectives are:
| \(A\) | \(B\) | \(A|B\) |
|---|---|---|
| \(\text{T}\) | \(\text{T}\) | \(\phi\) |
| \(\text{T}\) | \(\phi\) | \(\text{T}\) |
| \(\phi\) | \(\text{T}\) | \(\text{T}\) |
| \(\phi\) | \(\phi\) | \(\text{T}\) |
and
| \(A\) | \(B\) | \(A↓B\) |
|---|---|---|
| \(\text{T}\) | \(\text{T}\) | \(\phi\) |
| \(\text{T}\) | \(\phi\) | \(\phi\) |
| \(\phi\) | \(\text{T}\) | \(\phi\) |
| \(\phi\) | \(\phi\) | \(\text{T}\) |
Find an expression for \((A ∧ ¬B) ∨ C\) using only these new connectives (as well as negation and the variable symbols themselves)
The famous logician Raymond Smullyan devised a family of logical puzzles around a fictitious place he called “the Island of Knights and Knaves.” The inhabitants of the island are either knaves, who always make false statements, or knights, who always make truthful statements.
In the most famous knight/knave puzzle, you are in a room which has only two exits. One leads to certain death and the other to freedom. There are two individuals in the room, and you know that one of them is a knight and the other is a knave, but you don’t know which. Your challenge is to determine the door which leads to freedom by asking a single question.


