2.3: Logical Equivalences

Some logical statements are “the same.” For example, in the last section, we discussed the fact that a conditional and its contrapositive have the same logical content. Wouldn’t we be justified in writing something like the following?

$A \implies B = ¬B \implies ¬A$

Well, one pretty serious objection to doing that is that the equals sign $(=)$ has already got a job; it is used to indicate that two numerical quantities are the same. What we’re doing here is really sort of a different thing! Nevertheless, there is a concept of “sameness” between certain compound statements, and we need a symbolic way of expressing it. There are two notations in common use. The notation that seems to be preferred by logicians is the biconditional $(\iff)$. The notation we’ll use in the rest of this book is an equals sign with a bit of extra decoration on it $(\cong)$.

Thus we can either write

$(A \implies B) \iff (¬B \implies ¬A)$

or

$A \implies B \cong ¬B \implies ¬A.$

I like the latter, but use whichever form you like – no one will have any problem understanding either.

The formal definition of logical equivalence, which is what we’ve been describing, is this: two compound sentences are logically equivalent if in a truth table (that contains all possible combinations of the truth values of the predicate variables in its rows) the truth values of the two sentences are equal in every row.

Practice

Consider the two compound sentences $A ∨ B$ and $A ∨ (¬A ∧ B)$. There are a total of $2$ predicate variables between them, so a truth table with $4$ rows will suffice. Fill out the missing entries in the truth table and determine whether the statements are equivalent.

$A$	$B$	$A ∨ B$	$A ∨ (¬A ∧ B)$
$T$	$T$
$T$	$\phi$
$\phi$	$T$
$\phi$	$\phi$

One could, in principle, verify all logical equivalences by filling out truth tables. Indeed, in the exercises for this section, we will ask you to develop a certain facility at this task. While this activity can be somewhat fun, and many of my students want the filling-out of truth tables to be a significant portion of their midterm exam, you will probably eventually come to find it somewhat tedious. A slightly more mature approach to logical equivalences is this: use a set of basic equivalences – which themselves may be verified via truth tables – as the basic rules or laws of logical equivalence, and develop a strategy for converting one sentence into another using these rules. This process will feel very familiar, it is like “doing” algebra, but the rules one is allowed to use are subtly different.

First, we have the commutative laws, one each for conjunction and disjunction. It’s worth noting that there isn’t a commutative law for implication.

The commutative property of conjunction says that $A∧B \cong B ∧A$. This is quite an apparent statement from the perspective of linguistics. Surely it’s the same thing to say “the weather is cold and snowy” as it is to say “the weather is snowy and cold.” This commutative property is also clear from the perspective of digital logic circuits.

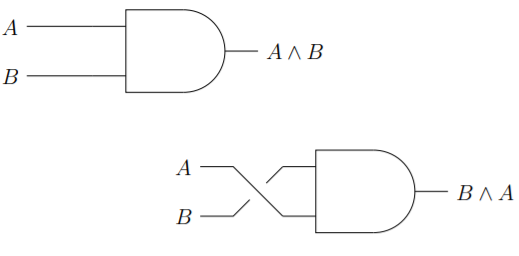
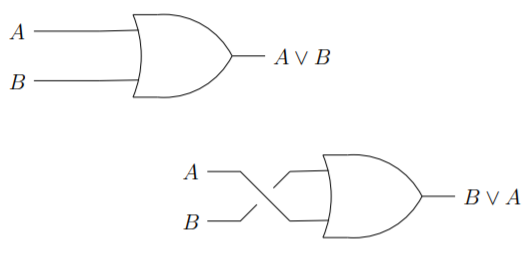
The commutative property of disjunctions is equally transparent from the perspective of a circuit diagram.

The associative laws also have something to do with what order operations are done. One could think of the difference in the following terms: Commutative properties involve spatial or physical order and the associative properties involve temporal order. The associative law of addition could be used to say we’ll get the same result if we add $2$ and $3$ first, then add $4$, or if we add $2$ to the sum of $3$ and $4$ (i.e. that $(2+3)+4$ is the same as $2+ (3+4)$.) Note that physically, the numbers are in the same order ($2$ then $3$ then $4$) in both expressions but that the parentheses indicate a precedence in when the plus signs are evaluated.

The associative law of conjunction states that $A∧(B ∧C) \cong (A∧B)∧C$. In visual terms, this means the following two circuit diagrams are equivalent.

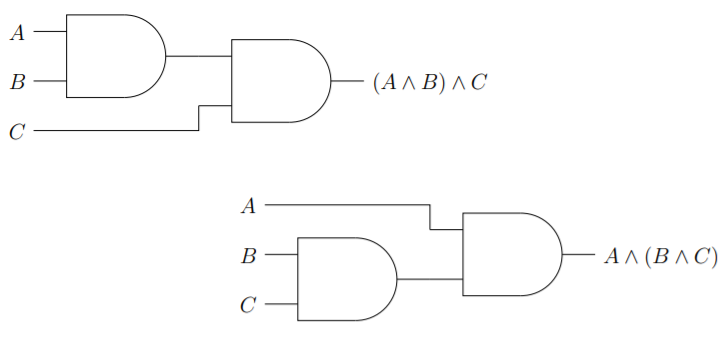
The associative law of disjunction states that $A∨(B ∨ C) \cong (A∨B)∨ C$. Visually, this looks like:

Note

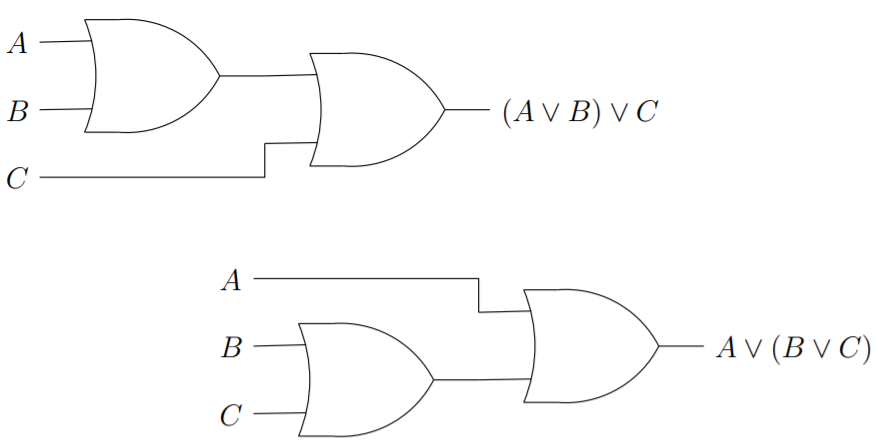
In a situation where both associativity and commutativity pertain the symbols involved can appear in any order and with any reasonable parenthesization. In how many different ways can the sum $2 + 3 + 4$ be expressed? Only consider expression that are fully parenthesized.

The next type of basic logical equivalences we’ll consider are the so-called distributive laws. Distributive laws involve the interaction of two operations, when we distribute multiplication over a sum, we effectively replace one instance of an operand and the associated operator, with two instances, as is illustrated below.

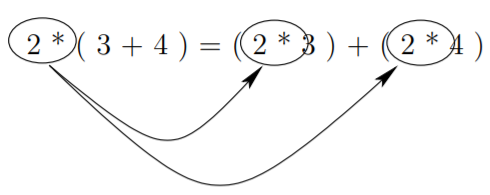
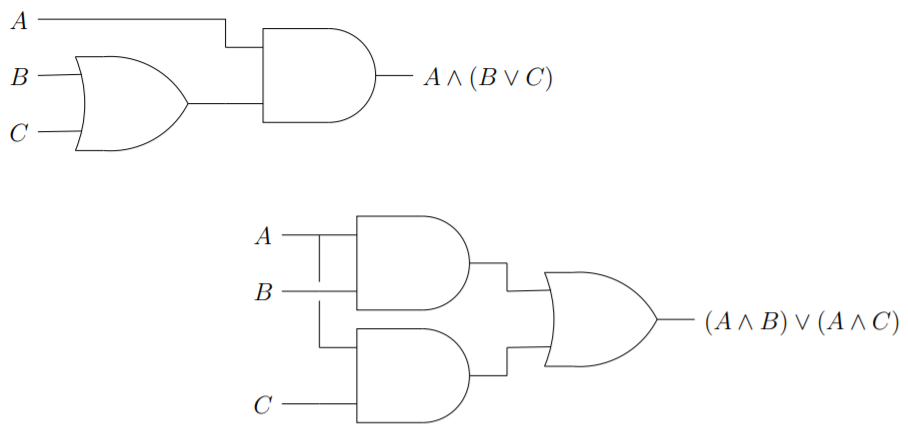
The logical operators ∧ and ∨ each distribute over the other. Thus we have the distributive law of conjunction over disjunction, which is expressed in the equivalence $A ∧ (B ∨ C) \cong (A ∧ B) ∨ (A ∧ C)$ and in the following digital logic circuit diagram.

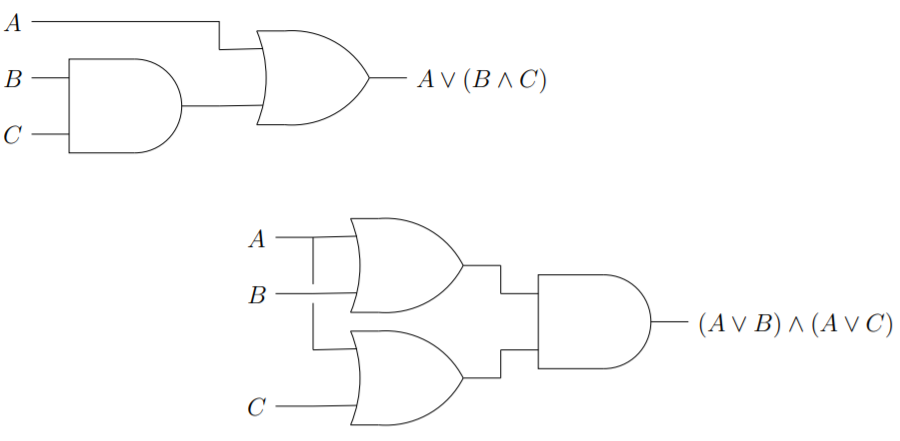
We also have the distributive law of disjunction over conjunction which is given by the equivalence $A ∨ (B ∧ C) \cong (A ∨ B) ∧ (A ∨ C)$ and in the circuit diagram:

Traditionally, the laws we’ve just stated would be called left-distributive laws and we would also need to state that there are right-distributive laws that apply. Since, in the current setting, we have already said that the commutative law is valid, this isn’t really necessary.

Practice

State the right-hand versions of the distributive laws.

The next set of laws we’ll consider come from trying to figure out what the distribution of a minus sign over a sum $(−(x + y) = −x + −y)$ should correspond to in Boolean algebra. At first blush, one might assume the analogous thing in Boolean algebra would be something like $¬(A∧B) \cong ¬A∧¬B$, but we can easily dismiss this by looking at a truth table.

$A$	$B$	$¬(A ∧ B)$	$¬A ∧ ¬B$
$T$	$T$	$\phi$	$\phi$
$T$	$\phi$	$T$	$\phi$
$\phi$	$T$	$T$	$\phi$
$\phi$	$\phi$	$T$	$T$

What actually works is a set of rules known as DeMorgan’s laws, which basically say that you distribute the negative sign but you also must change the operator. As logical equivalences, DeMorgan’s laws are

$¬(A ∧ B) \cong ¬A ∨ ¬B$

and

\(¬(A ∨ B) \cong ¬A ∧ ¬B.)

In ordinary arithmetic, there are two notions of “inverse.” The negative of a number is known as its additive inverse and the reciprocal of a number is its multiplicative inverse. These notions lead to a couple of equations,

$x + −x = 0$

and

$x · \dfrac{1}{x} = 1.$

Boolean algebra only has one “inverse” concept, the denial of a predicate (i.e. logical negation), but the equations above have analogues, as do the symbols $0$ and $1$ that appear in them. First, consider the Boolean expression $A ∨ ¬A$. This is the logical or of a statement and its exact opposite; when one is true the other is false and vice versa. But, the disjunction $A ∨ ¬A$, is always true! We use the symbol $t$ (which stands for tautology) to represent a compound sentence whose truth value is always true. A tautology ($t$) is to

Boolean algebra something like a zero ($0$) is to arithmetic. Similar thinking about the Boolean expression $A ∧ ¬A$ leads to the definition of the symbol $c$ (which stands for contradiction) to represent a sentence that is always false. The rules we have been discussing are known as complementarity laws:

$A ∨ ¬A \cong t$ and $A ∧ ¬A \cong c$

Now that we have the special logical sentences represented by $t$ and $c$ we can present the so-called identity laws, $A ∧ t \cong A$ and $A ∨ c \cong A$. If you “and” a statement with something that is always true, this new compound has the exact same truth values as the original. If you “or” a statement with something that is always false, the new compound statement is also unchanged from the original. Thus performing a conjunction with a tautology has no effect – sort of like multiplying by $1$. Performing a disjunction with a contradiction also has no effect – this is somewhat akin to adding $0$.

The number $0$ has a special property: $0 · x = 0$ is an equation that holds no matter what $x$ is. This is known as a domination property. Note that there isn’t a dominance rule that involves $1$. On the Boolean side, both the symbols $t$ and $c$ have related domination rules.

$A ∨ t \cong t$ and $A ∧ c \cong c$

In mathematics, the word idempotent is used to describe situations where the powers of a thing are equal to that thing. For example, because every power of $1$ is $1$, we say that $1$ is an idempotent. Both of the Boolean operations have idempotence relations that just always work (regardless of the operand). In ordinary algebra idempotents are very rare ($0$ and $1$ are the only ones that come to mind), but in Boolean algebra every statement is equivalent to its square – where the square of $A$ can be interpreted either as $A ∧ A$ or as $A ∨ A$.

$A ∨ A \cong A$ and $A ∧ A \cong A$

There are a couple of properties of the logical negation operator that should be stated, though probably they seem self-evident. If you form the denial of a denial, you come back to the same thing as the original; also the symbols $c$ and $t$ are negations of one another.

$¬(¬A) \cong A$ and $¬t \cong c$

Finally, we should mention a really strange property, called absorption, which states that the expressions $A∧(A∨B)$ and $A∨(A∧B)$ don’t actually have anything to do with $B$ at all! Both of the preceding statements are equivalent to $A$.

$A ∧ (A ∨ B) \cong A$ and $A ∨ (A ∧ B) \cong A$

In Table 2.3.1, we have collected all of these basic logical equivalences in one place.

Table 2.3.1: Basic Logical Equivalences.
	Conjunctive Version	Disjunctive Version	Algebraic Analog
Commutative Laws	$A∧B≅B∧A$	$A∨B≅B∨A$	$2+3=3+2$
Associative Laws	$A∧(B∧C)A∧(B∧C) ≅(A∧B)∧C$	$A∨(B∨C)A∨(B∨C) ≅(A∨B)∨C$	$2+(3+4)2+(3+4) =(2+3)+4$
Distributive Laws	$A∧(B∨C)≅A∧(B∨C)≅ \\(A∧B)∨(A∧C)$	$A∨(B∧C) ≅ \\ (A∨B)∧(A∨C)$	$2⋅(3+4)2⋅(3+4) =(2⋅3+2⋅4)$
DeMorgan's Laws	$¬(A∧B)¬(A∧B) ≅¬A∨¬B$	$¬(A∨B)¬(A∨B) ≅¬A∧¬B$	$\text{none}$
Double Negation	$¬(¬A)≅A$	$\text{same}$	$−(−2)=2$
Complementarity	$A∧¬A≅c$	$A∨¬A≅t$	$2+(−2)=0$
Identity Laws	$A∧t≅A$	$A∨c≅A$	$7+0=7$
Domination	$A∧c≅c$	$A∨t≅t$	$7⋅0=0$
Idempotence	$A∧A≅A$	$A∨A≅A$	$1⋅1=1$
Absorption	$A∧(A∨B)≅A$	$A∨(A∧B)≅A$	$\text{none}$

Exercises:

Exercise $\PageIndex{1}$

There are $3$ operations used in basic algebra (addition, multiplication and exponentiation) and thus there are potentially $6$ different distributive laws. State all $6$ “laws” and determine which $2$ are actually valid. (As an example, the distributive law of addition over multiplication would look like $x + (y · z) = (x + y) · (x + z)$, this isn’t one of the true ones.)

Exercise $\PageIndex{2}$

Use truth tables to verify or disprove the following logical equivalences.

1. $(A ∧ B) ∨ B \cong (A ∨ B) ∧ B$
2. $A ∧ (B ∨ ¬A) \cong A ∧ B$
3. $(A ∧ ¬B) ∨ (¬A ∧ ¬B) \cong (A ∨ ¬B) ∧ (¬A ∨ ¬B)$
4. The absorption laws.

Exercise $\PageIndex{3}$

Draw pairs of related digital logic circuits that illustrate DeMorgan’s laws.

Exercise $\PageIndex{4}$

Find the negation of each of the following and simplify as much as possible.

$(A ∨ B) \iff C$

$(A ∨ B) \implies (A ∧ B)$

Exercise $\PageIndex{5}$

Because a conditional sentence is equivalent to a certain disjunction, and because DeMorgan’s law tells us that the negation of a disjunction is a conjunction, it follows that the negation of a conditional is a conjunction. Find denials (the negation of a sentence is often called its “denial”) for each of the following conditionals.

1. “If you smoke, you’ll get lung cancer.”
2. “If a substance glitters, it is not necessarily gold.”
3. “If there is smoke, there must also be fire.”
4. “If a number is squared, the result is positive.”
5. “If a matrix is square, it is invertible.”

Exercise $\PageIndex{6}$

The so-called “ethic of reciprocity” is an idea that has come up in many of the world’s religions and philosophies. Below are statements of the ethic from several sources. Discuss their logical meanings and determine which (if any) are logically equivalent.

1. “One should not behave towards others in a way which is disagreeable to oneself.” Mencius Vii.A.4 (Hinduism)
2. “None of you [truly] believes until he wishes for his brother what he wishes for himself.” Number 13 of Imam “Al-Nawawi’s Forty Hadiths.” (Islam)
3. “And as ye would that men should do to you, do ye also to them likewise.” Luke 6:31, King James Version. (Christianity)
4. “What is hateful to you, do not to your fellow man. This is the law: all the rest is commentary.” Talmud, Shabbat 31a. (Judaism)
5. “An it harm no one, do what thou wilt” (Wicca)
6. “What you would avoid suffering yourself, seek not to impose on others.” (the Greek philosopher Epictetus – first century A.D.)
7. “Do not do unto others as you expect they should do unto you. Their tastes may not be the same.” (the Irish playwright George Bernard Shaw – $20^{\text{th}}$ century A.D.)

Exercise $\PageIndex{7}$

You encounter two natives of the land of knights and knaves. Fill in an explanation for each line of the proofs of their identities.

1. Natasha says, “Boris is a knave.” Boris says, “Natasha and I are knights."

Claim: Natasha is a knight, and Boris is a knave.

Proof: If Natasha is a knave, then Boris is a knight.

If Boris is a knight, then Natasha is a knight.

Therefore, if Natasha is a knave, then Natasha is a knight.

Hence Natasha is a knight.

Therefore, Boris is a knave.

Q.E.D.

2. Bonaparte says “I am a knight and Wellington is a knave.” Wellington says “I would tell you that B is a knight.”

Claim: Bonaparte is a knight and Wellington is a knave.

Proof: Either Wellington is a knave or Wellington is a knight.

If Wellington is a knight it follows that Bonaparte is a knight.

If Bonaparte is a knight then Wellington is a knave.

So, if Wellington is a knight then Wellington is a knave (which is impossible!)

Thus, Wellington is a knave.

Since Wellington is a knave, his statement “I would tell you that Bonaparte is a knight” is false.

So Wellington would in fact tell us that Bonaparte is a knave.

Since Wellington is a knave we conclude that Bonaparte is a knight.

Thus Bonaparte is a knight and Wellington is a knave (as claimed).

Q.E.D.