4.3: Set Operations
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section, we’ll continue to develop the correspondence between Logic and Set theory.
The logical connectors ∧ and ∨ correspond to the set-theoretic notions of union (∪) and intersection (∩). The symbols are designed to provide a mnemonic for the correspondence; the Set theory symbols are just rounded versions of those from Logic.
Explicitly, if P(x) and Q(x) are open sentences, then the union of the corresponding truth sets SP and SQ is defined by
SP∪SQ={x∈UP(x)∨Q(x)}.
Suppose two sets A and B are given. Re-express the previous definition of “union” using their membership criteria, MA(x)=“x∈A” and MB(x)=“x∈B.”
The union of more than two sets can be expressed using a big union symbol. For example, consider the family of real intervals defined by In=(n,n+1].1 There’s an interval for every integer n. Also, every real number is in one of these intervals. The previous sentence can be expressed as
R=⋃n∈ZIn.
The intersection of two sets is conceptualized as “what they have in common” but the precise definition is found by considering conjunctions,
A∩B={x∈Ux∈A∧x∈B}.
With reference to two open sentences P(x) and Q(x), define the intersection of their truth sets, SP∩SQ.
There is also a “big” version of the intersection symbol. Using the same family of intervals as before,
∅=⋂n∈ZIn.
Of course, the intersection of any distinct pair of these intervals is empty so the statement above isn’t particularly strong.
Negation in Logic corresponds to complementation in Set theory. The complement of a set A is usually denoted by ¯A (although some prefer a superscript c – as in Ac), this is the set of all things that aren’t in A. In thinking about complementation one quickly sees why the importance of working within a well-defined universal set is stressed. Consider the set of all math textbooks. Obviously, the complement of this set would contain texts in English, Engineering and Evolution – but that statement is implicitly assuming that the universe of discourse is “textbooks.” It’s equally valid to say that a very long sequence of zeros and ones, a luscious red strawberry, and the number √π are not math textbooks and so these things are all elements of the complement of the set of all math textbooks. What is really a concern for us is the issue of whether or not the complement of a set is well-defined, that is, can we tell for sure whether a given item is or is not in the complement of a set. This question is decidable exactly when the membership question for the original set is decidable. Many people think that the main reason for working within a fixed universal set is that we then have well-defined complements. The real reason that we accept this restriction is to ensure that both membership criteria, MA(x) and M¯A(x), are decidable open sentences. As an example of the sort of strangeness that can crop up, consider that during the time that I, as the author of this book, was writing the last paragraph, this text was nothing more than a very long sequence of zeros and ones in the memory of my computer. . .
Every rule that we learned in Chapter 2 (see Table 2.3.1) has a set-theoretic equivalent. These set-theoretic versions are expressed using equalities (i.e. the symbol = in between two sets) which is actually a little bit funny if you think about it. We normally use = to mean that two numbers or variables have the same numerical magnitude, as in 122=144, we are doing something altogether different when we use that symbol between two sets, as in {1,2,3}={√1,√4,√9}, but people seem to be used to this so there’s no sense in quibbling.
Develop a useful definition for set equality. In other words, come up with a (quantified) logical statement that means the same thing as “A=B” for two arbitrary sets A and B.
What symbol in Logic should go between the membership criteria MA(x) and MB(x) if A and B are equal sets?
In Table 4.3.1 the rules governing the interactions between the set-theoretic operations are collected.
We are now in a position somewhat similar to when we jumped from proving logical assertions with truth tables to doing two-column proofs. We have two different approaches for showing that two sets are equal. We can do a so-called “element chasing” proof (to show A=B, assume x∈A and prove x∈B and then vice versa). Or, we can construct a proof using the basic set equalities given in Table 4.3.1. Often the latter can take the form of a two-column proof.
| Table 4.3.1: Basic Set Theoretic Equalities | ||
|---|---|---|
| ∩ | ∪ | |
| Commutative Laws | A∩B=B∩A | A∪B=B∪A |
| Associative Laws | A∩(B∩C)=(A∩B)∩C | A∪(B∪C)=(A∪B)∪C |
| Distributive Laws | A∩(B∪C)=(A∩B)∪(A∩C) | A∪(B∩C)=(A∪B)∩(A∪C) |
| DeMorgan's Laws | ¯A∩B=¯A∪¯B | ¯A∪B=¯A∩¯B |
| Double Complement | ¯¯A=A | same |
| Complementarity | A∩¯A=∅ | A∪¯A=U |
| Identity Laws | A∩U=A | A∪∅=A |
| Domination | A∩∅=∅ | A∪U=U |
| Idempotence | A∩A=A | A∪A=A |
| Absorption | A∩(A∪B)=A | A∪(A∩B)=A |
Before we proceed much further in our study of set theory it would be a good idea to give you an example. We’re going to prove the same assertion in two different ways — once via element chasing and once using the basic set-theoretic equalities from Table 4.3.1.
The statement we’ll prove is A∪B=A∪(A∩B).
First, by chasing elements:
Proof: Suppose x is an element of A∪B. By the definition of union we know that
x∈A∨x∈B.
The conjunctive identity law and the fact that x∈A∨x∉A is a tautology gives us an equivalent logical statement: (x∈A∨x∉A)∧(x∈A∨x∈B).
Finally, this last statement is equivalent to
x∈A∨(x∉A∧x∈B)
which is the definition of x∈A∪(A∩B).
On the other hand, if we assume that x∈A∪(A∩B), it follows that
x∈A∨(x∉A∧x∈B).
Applying the distributive law, disjunctive complementarity and the identity law, in sequence we obtain
∈A∨(x∉A∧x∈B)≅(x∈A∨x∉A)∧(x∈A∨x∈B)≅t∧(x∈A∨x∈B)≅x∈A∨x∈B
The last statement in this chain of logical equivalences provides the definition of x∈A∪B.
Q.E.D.
A two-column proof of the same statement looks like this:
Proof:
A∪B
=U∩(A∪B)
=(A∪A)∩(A∪B)
=(A∪(A∩B)
Q.E.D.
There are some notions within Set theory that don’t have any clear parallels in Logic. One of these is essentially a generalization of the concept of “complements.” If you think of the set A as being the difference between the universal set U and the set A you are on the right track. The difference between two sets is written A∖B (sadly, sometimes this is denoted using the ordinary subtraction symbol A−B) and is defined by
A∖B=A∩¯B.
The difference, A∖B, consists of those elements of A that aren’t in B. In some developments of Set theory, the difference of sets is defined first and then complementation is defined by A=U∖A.
The difference of sets (like the difference of real numbers) is not a commutative operation. In other words A∖B≠B∖A (in general). It is possible to define an operation that acts somewhat like the difference, but that is commutative. The symmetric difference of two sets is denoted using a triangle (really a capital Greek delta).
A△B=(A∖B)∪(B∖A).
Show that A△B=(A∪B)∖(A∩B).
Come on! You read right past that exercise without even pausing!
What? You say you did try it and it was too hard?
Okay, just for you (and this time only) I’ve prepared an aid to help you through. . .
On the next page is a two-column proof of the result you need to prove, but the lines of the proof are all scrambled. Make a copy and cut out all the pieces and then glue them together into a valid proof.
So, no more excuses, just do it!
| =(A∩B)∪(B∩A) | Identity Law |
| =(A∪B)∩(A∩B) | Def. of Relative Difference |
| (A∪B)∖(A∩B) | Given |
| =((A∩A)∪(A∩B))∪((B∩A)∪(B∩B)) | Distributive Law |
| =(A∖B)∪(B∖A) | Def. of Relative Difference |
| =(A∩(A∩B))∪(B∩(A∩B)) | Distributive Law |
| =A△B | Def. of Relative Difference |
| =(A∩(A∪B)∪(B∩(A∪B)) | DeMorgan's Law |
| =(∅∪(A∩B))∪((B∩A)∪∅) | Complementarity |
Exercises:
Let A={1,2,{1,2},b} and let B={a,b,{1,2}}. Find the following:
- A∩B
- A∪B
- A∖B
- B∖A
- A△B
In a standard deck of playing cards, one can distinguish sets based on face-value and/or suit. Let A,2,...9,10,J,Q and K represent the sets of cards having the various face-values. Also, let ♥,♠,♣ and ♦ be the sets of cards having the possible suits. Find the following
- A∩♥
- A∪♥
- J∩(♠∪♥)
- K∩♥
- A∩K
- A∪K
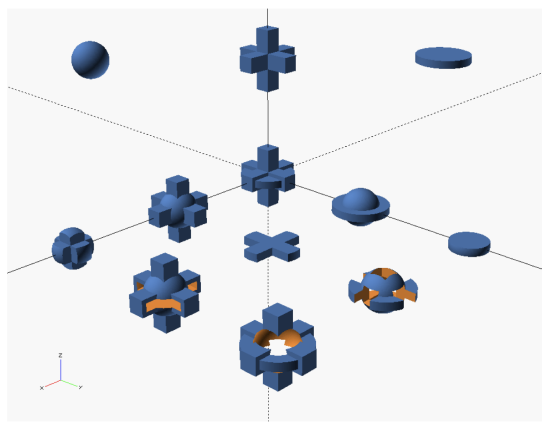
The following is a screenshot from the computational geometry program OpenSCAD (very handy for making models for 3-d printing. . . ) In computational geometry, we use the basic set operations together with a few other types of transformations to create interesting models using simple components. Across the top of the image below we see 3 sets of points in R3, a ball, a sort of 3-dimensional plus sign, and a disk. Let’s call the ball A, the plus sign B and the disk C. The nine shapes shown below them are made from A, B and C using union, intersection and set difference. Identify them!
Do element-chasing proofs (show that an element is in the left-hand side if and only if it is in the right-hand side) to prove each of the following set equalities.
- A∩B=A∪B
- A∪B=A∪(A∩B)
- A△B=(A∪B)∖(A∩B)
- (A∪B)∖C=(A∖C)∪(B∖C)
For each positive integer n, we’ll define an interval In by
In=[−n,1n).
Find the union and intersection of all the intervals in this infinite family.
⋃n∈Z+In=
⋂n∈Z+In=
There is a set X such that, for all sets A, we have X△A=A. What is X?
There is a set Y such that, for all sets A, we have Y△A=A. What is Y?
In proving a set-theoretic identity, we are basically showing that two sets are equal. One reasonable way to proceed is to show that each is contained in the other. Prove that A∩(B∪C)=(A∩B)∪(A∩C) by showing that A∩(B∪C)⊆(A∩B)∪(A∩C)and(A∩B)∪(A∩C)⊆A∩(B∪C).
Prove that A∪(B∩C)=(A∪B)∩(A∪C) by showing that A∪(B∩C)⊆(A∪B)∩(A∪C) and (A∪B)∩(A∪C)⊆A∪(B∩C).
Prove the set-theoretic versions of DeMorgan’s laws using the technique discussed in the previous problems.
The previous technique (showing that A=B by arguing that A⊆B∧B⊆A) will have an outline something like
Proof: First we will show that A⊆B.
Towards that end, suppose x∈A. . . .
Thus x∈B.
Now, we will show that B⊆A.
Suppose that x∈B. . . .
Thus x∈A.
Therefore A⊆B∧B⊆A so we conclude that A=B.
Q.E.D.
Formulate a proof that A△B=(A∪B)∖(A∩B) that follows this outline.



