3.3: Operations on Sets
- Page ID
- 23893
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)There are several important ways that a new set can be made from sets that you already have. Any method of doing this is called a set operation.
3.3A. Union and Intersection.
Two of the most basic operations are union and intersection. Let us first discuss them in informal terms. Suppose:
- Alice and Bob are going to have a party, and need to decide who should be invited,
- Alice made a list of all the people that she would like to invite, and
- Bob made a list of all the people that he would like to invite.
Here are two of the many possible decisions they could make.
- One solution would be to invite everyone that is on either of the lists. That is, they could begin their invitation list by writing down all of the names on Alice’s list, and then add all of the names from Bob’s list (or, more precisely, the names from Bob’s list that are not already included in Alice’s list). This is the union of the lists.
- A much more conservative solution would be to invite only the people that appear on both of the lists. That is, they could go through Alice’s list, and cross off everyone that does not appear on Bob’s list. (They would get the same result by going through Bob’s list, and crossing off everyone that does not appear on Alice’s list.) This is the intersection of the lists.
Suppose \(A\) and \(B\) are sets.
- The union of \(A\) and \(B\) is the set \[A \cup B=\{x \mid x \in A \text { or } x \in B\} .\]
- The intersection of \(A\) and \(B\) is the set \[A \cap B = \{A \cap B=\{x \mid x \in A \text { and } x \in B\} .\]
By drawing the sets \(A\) and \(B\) as overlapping circles, the union and intersection can be represented as follows:
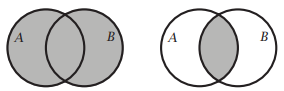
\(A \cup B\) is shaded \(A \cap B\) is shaded
Pictures like these are called Venn diagrams.
- In ordinary English, the word “intersection” refers to where two things meet. For example, the intersection of two streets is where the two streets come together. We can think of this area as being part of both streets, so this is consistent with the way the term is used in mathematics.
- In ordinary English, the word “union” refers to joining things together. For example, a marriage is the union of two people — it joins the two people into a single married couple. This is consistent with the way the term is used in mathematics — we could form the union of Alice’s list and Bob’s list by gluing Bob’s list to the end of Alice’s list.
- \(\{1,3,5,7,9\} \cup \{1,4,7,10\} = \{1,3,4,5,7,9,10\}\)
- \(\{1,3,5,7,9\} \cap \{1,4,7,10\} = \{1,7\}\)
Solution
Add text here.
Specify each set by listing its elements. (You do not need to show your work.)
- \(\{1,2,3,4\} \cup\{3,4,5,6,7\}=\)
- \(\{1,2,3,4\} \cap\{3,4,5,6,7\}=\)
- \(\{\mathrm{p}, \mathrm{r}, \mathrm{o}, \mathrm{n}, \mathrm{g}\} \cap\{\mathrm{h}, \mathrm{o}, \mathrm{r}, \mathrm{n}, \mathrm{s}\}=\)
- \(\{\mathrm{p}, \mathrm{r}, \mathrm{o}, \mathrm{n}, \mathrm{g}\} \cup\{\mathrm{h}, \mathrm{o}, \mathrm{r}, \mathrm{n}, \mathrm{s}\}=\)
- \((\{1,3,5\} \cup\{2,3,4\}) \cap\{2,4,6\}=\)
- \((\{1,3,5\} \cap\{2,3,4\}) \cup\{2,4,6\}=\)
- Assume \(A\) and \(B\) are sets. Prove that if \(c \in A \cap B\), then \(c \in A\).
- Assume \(X\), \(Y\), and \(Z\) are sets. Prove that if \(r \in (X \cap Y) \cup (X \cap Z)\), then \(r \in X\).
- It is not difficult to see that \(\cup\) and \(\cap\) are commutative. That is, for all sets \(A\) and \(B\), we have \[A \cup B=B \cup A \quad \text { and } \quad A \cap B=B \cap A\]
-
It is also not difficult to see that \(\cup\) and \(\cap\) are associative. That is, for all sets \(A\), \(B\), and \(C\), we have \[(A \cup B) \cup C=A \cup(B \cup C) \quad \text { and } \quad(A \cap B) \cap C=A \cap(B \cap C)\]
So there is no need for parenthesis when writing \(A \cup B \cup C\) or \(A \cap B \cap C\). (However, you do need parentheses when writing something like \(A \cup (B \cap C)\) or \((A \cup B) \cap C\), which uses both \(\cup\) and \(\cap\).)
A Venn diagram can include more than two sets. For example, here are Venn diagrams of \(A \cap B \cap C\) and \(A \cap (B \cup C)\).
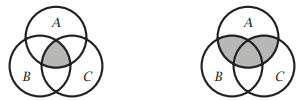
\(A \cap B \cap C\) is shaded \(A \cap (B \cup C)\) is shaded
Solution
Add text here.
Draw a Venn diagram of each set. (You do not need to show your work.)
- \(A \cup B \cup C\)
- \(A \cup(B \cap C)\)
- \((A \cup B) \cap C\)
- \((A \cap C) \cup(B \cap C)\)
- Answer
-
Add texts here. Do not delete this text first.
3.3B. Set Difference and Complement
The “set difference” is another fundamental operation.
If there is a list of people that Alice would like to invite to the party, and also a list of people that Bob refuses to allow to come to the party (the “veto list”), then it would be reasonable to invite the people that are on Alice’s list, but not on the veto list. That is, they could start with Alice’s list, and remove all of the names that are on Bob’s list. This is the set difference of Alice’s list and Bob’s list.
Suppose \(A\) and \(B\) are sets.
- The set difference of \(A\) and \(B\) is the set \[A \backslash B=\{x \in A \mid x \notin B\}=\{x \mid(x \in A) \&(x \notin B)\} .\]
-
The complement of \(B\) is the set \[\bar{B}=\mathcal{U} \backslash B=\{x \mid x \notin B\}\]
where \(\mathcal{U}\) is the universal set, as usual.
Some authors write \(A - B\), instead of \(A \backslash B\). Also, some authors write \(B^{c}\), instead of \(\bar{B}\)
Here are Venn diagrams.
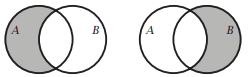
\(A \backslash B\) is shaded \(B \backslash A\) is shaded
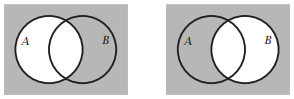
\(\bar{A}\) is shaded \(\bar{B}\) is shaded
Suppose \(\mathcal{U}=\mathrm{PEOPLE}\) is the set of all people.
- \(\overline{\text { CHILDREN }}=\text { ADULTS }\), because adults are the people who are not children.
- \(\text { FEMALES } \backslash \text { CHILDREN }\) is the set of all adult women.
Assume \(\mathcal{U}=\{1,2,3, \ldots, 10\}\). Specify each set by listing its elements. (You do not need ot show your work.)
- \(\{1,3,5,7,9\} \backslash\{4,5,6,7\}=\)
- \(\{4,5,6,7\} \backslash\{1,3,5,7,9\}=\)
- \(\overline{\{1,3,5,7,9\}}=\)
- \(\overline{\{4,5,6,7\}}=\)
Draw a Venn diagram of each set. (You do not need to show your work.)
- \(\overline{A \cup B}\)
- \(\overline{A \cap B}\)
- \((A \vee B) \backslash(A \vee C)\)
- \(A \backslash(B \backslash C)\)
- \((A \cup B) \backslash C\)
Suppose \(A\) and \(B\) are sets. Show that if \(c \in \overline{A \cup B}\), then \(c \in \bar{A} \cap \bar{B}\).
Solution
Assume \(c \in \overline{A \cup B}\). By definition of the complement, this means \(c \notin A \cup B\). In other words, it is not true that \(c \in A \cup B\). From the definition of \(A \cup B\), we conclude that \[\text { it is not true that either } c \in A \text { or } c \in B \text {. }\]
By the rules of negation, this means \(c \notin A\) and \(c \notin B\). Now:
- since \(c \notin A\), we have \(c \in \bar{A},\), and
- since \(c \notin B\), we have \(c \in \bar{B}\).
Therefore, we know \(c \in \bar{A}\) and \(c \in \bar{B}\), so \(c \in \bar{A} \cap \bar{B}\).
Suppose \(A\) and \(B\) are sets. Show that if \(c \in \bar{A} \cap \bar{B}\), then \(c \in \overline{A \cup B}\).
3.3C. Disjoint sets
Two sets \(A\) and \(B\) are said to be disjoint iff their intersection is empty (that is, \(A \cap B=\varnothing\)). In other words, they have no elements in common: \[A \text { and } B \text { are disjoint } \Leftrightarrow \begin{gathered}
\text { there does not exist an } x, \\
\text { such that }((x \in A) \&(x \in B)) .
\end{gathered}\]
We may also say that \(A\) is disjoint from B.
- The sets \(\{1,3,5\}\) and \(\{2,4,6\}\) are disjoint, because they have no elements in common.
- The sets \(\{1,3,5\}\) and \(\{2,3,4\}\) are not disjoint, because \(3\) is in their intersection.
- The following Venn diagram illustrates two disjoint sets \(A\) and \(B\) (they do not overlap):
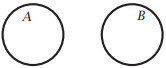
\(A\) and \(B\) are disjoint
Let us point out some well-known facts that will be formally proved in Chapter \(9\).
- If \(A\) and \(B\) are two disjoint sets, then \(\#(A \cup B)=\# A+\# B\).
- The situation is similar even if there are more than \(2\) sets: Suppose \(A_1,A_2,\ldots,A_n\) are pairwise-disjoint sets. (This means that \(A_i\) is disjoint from \(A_j\) whenever \(i \neq j\).) Then \[\#\left(A_{1} \cup A_{2} \cup \cdots \cup A_{n}\right)=\# A_{1}+\# A_{2}+\cdots+\# A_{n} .\]
- If \(A\) and \(B\) are two finite sets that are not disjoint, then \(\#(A \cup B)<\# A+\# B\).
3.3D. The Power Set.
It is not difficult to list all of the subsets of \(\{a,b,c\}\). One way to do this is to consider the possible number of elements in the subset:
- A subset with \(0\) elements has no elements at all. It must be the empty set \(\varnothing\).
- Consider a subset with \(1\) element. That one element must be one of the elements of \(\{a,b,c\}\). That is, the element of the set must be \(a\), \(b\), or \(c\). So the 1-element subsets are \(\{a\}\), \(\{b\}\), and \(\{c\}\).
- Consider the subsets with \(2\) elements.
- If \(a\) is one of the elements in the subset, then the other element must be either \(b\) or \(c\).
- If \(a\) is not in the subset, then the subset must contain both \(b\) and \(c\).
Hence, the \(2\)-element subsets are \(\{a,b\}\), \(\{a,c\}\), and \(\{b,c\}\).
- A subset with \(3\) elements must have all of the elements of \(\{a,b,c\}\), so the subset must be \(\{a,b,c\}\).
- Because \(\{a,b,c\}\) has only \(3\) elements, we know that no subset can have more than \(3\) elements.
Thus, the subsets of \(\{a,b,c\}\) are \[\varnothing,\{a\},\{b\},\{c\},\{a, b\},\{a, c\},\{b, c\},\{a, b, c\} .\]
Counting them, we see that there are exactly \(8\) subsets.
In general, one can show that any set with \(n\) elements has exactly \(2^{n}\) subsets. In the above example, we have \(n = 3\), and the number of subsets is \(2^{3} = 8\).
(You do not need to show your work.)
- List the subsets of \(\{a\}\).
- List the subsets of \(\{a,b\}\).
- List the subsets of \(\{a,b,c,d\}\).
- List the subsets of \(\varnothing\).
We can make a set by putting set braces at the ends of the above list of subsets of \(\{a,b,c\}\): \[\{\varnothing,\{a\},\{b\},\{c\},\{b, c\},\{a, c\},\{a, b\},\{a, b, c\}\} .\]
In general, the set of all subsets of a set is called its power set:
Suppose \(A\) is a set. The power set of \(A\) is the set of all subsets of \(A\). It is denoted \(\mathcal{P}(A)\). This means \[\mathcal{P}(A)=\{B \mid B \subset A\} .\]
From Remark \(3.3.22\)., we see that if \(\#A = n\), then \(\# \mathcal{P}(A)=2^{n}\). This formula involving “two-to-the-\(n\)th-power” can be considered a justification for calling \(\mathcal{P}(A)\) the power set.
- Describe each of the following sets by listing its elements.
(You do not need to show your work.)- \(\mathcal{P}(\varnothing)\)
- \(\mathcal{P}(\{\mathrm{a}\})\)
- \(\mathcal{P}(\{\mathrm{a}, \mathrm{b}\})\)
- \(\mathcal{P}(\{\mathrm{a}, \mathrm{b}, \mathrm{c}\})\)
- \(\mathcal{P}(\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}\})\)
- Which of the following are elements of \(\mathcal{P}(\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}\})\)?
(You do not need to show your work.)- \(a\)
- \(\{\mathrm{a}\}\)
- \(\{a, b\}\)
- \(\{\mathrm{a}, \mathrm{c}\}\)
- Suppose \(A\) is a set.
- Is \(\varnothing \in \mathcal{P}(A)\)? Why?
- Is \(A \in \mathcal{P}(A)\)? Why?
- Does there exist a set \(A\), such that \(\mathcal{P}(A)=\varnothing\)?
- Let \[V_{0}=\varnothing, \quad V_{1}=\mathcal{P}\left(V_{0}\right), \quad V_{2}=\mathcal{P}\left(V_{1}\right)=\mathcal{P}\left(\mathcal{P}\left(V_{0}\right)\right), \quad \text { and so forth. }\]
In general, \(V_{n}=\mathcal{P}\left(V_{n-1}\right)\) whenever \(n > 0\).- What are the cardinalities of \(V_{0}\), \(V_{1}\), \(V_{2}\), \(V_{3}\), \(V_{4}\), and \(V_{5}\)?
- Describe \(V_{0}\), \(V_{1}\), \(V_{2}\), and \(V_{3}\) by listing their elements.
- (harder) Describe \(V_{4}\) by listing its elements.
- Is it reasonable to ask someone to list the elements of \(V_{5}\)? Why?


