6.7: Inverse Functions

Backwards poets write inverse.

Author unknown

All students of mathematics have experience with solving an equation for \(x\). Inverse functions are a special case of this.

Example \(6.7.1\).

In Example \(6.6.6\), it was shown that \(f(x) = 5x − 7\) is a bijection. A look at the proof reveals that the formula \((y + 7)/5\) plays a key role. The reason this formula is so important is that (solving for \(x\)) we have \[y=5 x-7 \quad \Leftrightarrow \quad x=\frac{y+7}{5} .\]

In order to see this as an “inverse function,” we translate into the language of functions, by letting \(g: \mathbb{R} \rightarrow \mathbb{R}\) be defined by \(g(y) = (y + 7)/5\). Then the above assertion can be restated as: (6.7.2) \[y=f(x) \quad \Leftrightarrow \quad x=g(y) .\]

This tells us that \(g\) does exactly the opposite of what \(f\) does: if \(f\) takes \(x\) to \(y\), then \(g\) takes \(y\) to \(x\). We will say that \(g\) is the “inverse” of \(f\).

The following exercise provides a restatement of (6.7.2) that will be used in the official definition of inverse functions. However, we usually use \(A\) for the domain of a generic function (and \(B\) for the codomain), so it replaces the variables \(x\) and \(y\) with \(a\) and \(b\).

Exercise \(6.7.3\).

Suppose \(f: A \rightarrow B\) and \(g: B \rightarrow A\). Show that if \[\forall a \in A, \forall b \in B,(b=f(a) \Leftrightarrow a=g(b)) ,\]

then

1. \(g(f(a))=a \text { for all } a \in A\) and
2. \(\text { b) } f(g(b))=b \text { for all } b \in B \text {. }\)

Definition \(6.7.4\).

Suppose

• \(f: A \rightarrow B\), and
• \(g: B \rightarrow A\).

We say that \(g\) is the inverse of \(f\) iff:

1. \(g(f(a)) = a \text { for all } a \in A\), and
2. \(f(g(b))=b \text { for all } b \in B\)

Example \(6.7.5\).

Suppose \(z: S \rightarrow T\) and \(k: T \rightarrow S\). What does it mean to say that \(k\) is the inverse of \(z\)?

Solution

It means that two things are true:

1. \(k(z(s)) = s \text { for all } s \in S\), and
2. \(z(k(t))=t \text { for all } t \in T .\)

Exercise \(6.7.6\).

Suppose \(c: U \rightarrow V\) and \(d: V \rightarrow U\). What does it mean to say that \(d\) is the inverse of \(c\)?

Notation \(6.7.7\).

The inverse of \(f\) is denoted \(f^{−1}\).

Example \(6.7.8\).

Note that:

• the husband of the wife of any married man is the man himself, i.e., \[\text { husband }(\text { wife }(m))=m ,\]
  and
• the wife of the husband of any married woman is the woman herself, i.e., \[\text { wife }(\text { husband }(w))=w .\]

This means the \(\text {husband}\) function is the inverse of the \(\text {wife}\) function. That is, \(\text{wife}^{−1} = \text{ husband.}\)

Remark \(6.7.9\).

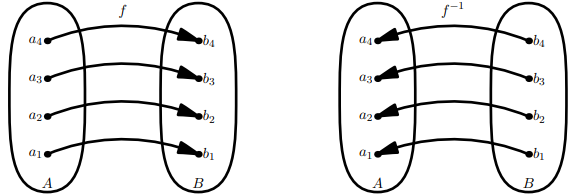
The inverse is easy to describe in terms of arrow diagrams. Namely, from the fact that \[b=f(a) \quad \Leftrightarrow \quad a=f^{-1}(b) ,\]

we see that \[f \text { has an arrow from } a \text { to } b \Leftrightarrow f^{-1} \text { has an arrow from } b \text { to } a \text {. } .\]

Therefore, the arrow diagram of \(f^{−1}\) is obtained by just reversing all the arrows in the arrow diagram of \(f\):

Example \(6.7.10\).

Define \(f: \mathbb{R} \rightarrow \mathbb{R}\) and \(g: \mathbb{R} \rightarrow \mathbb{R}\) by \(f(x) = 7x − 4\) and \(g(x) = (x + 4)/7\). Verify that \(g\) is the inverse of \(f\).

Solution

It suffices to show:

1. \(g(f(x))=x \text { for all } x \in \mathbb{R}\), and
2. \(f(g(y))=y \text { for all } y \in \mathbb{R} .\)

1. Given \(x \in \mathbb{R}\), we have \[g(f(x))=\frac{f(x)+4}{7}=\frac{(7 x-4)+4}{7}=\frac{7 x}{7}=x .\]
2. Given \(y \in \mathbb{R}\), we have \[f(g(y))=7 g(y)-4=7\left(\frac{y+4}{7}\right)-4=(y+4)-4=y .\]

Exercise \(6.7.11\).

In each case, verify that \(g\) is the inverse of \(f\).

1. \(f: \mathbb{R} \rightarrow \mathbb{R} \text { is defined bv } f(x)=9 x-6 \text { and } g: \mathbb{R} \rightarrow \mathbb{R} \text { is defined by } g(x)=(x+6) / 9 .\)
2. \(f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+} \text {is defined by } f(x)=x^{2} \text { and } g: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+} \text {is defined by } g(x)=\sqrt{x} .\)
3. \(f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+} \text {is defined by } f(x)=1 / x \text { and } g: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+} \text {is defined by } g(x)=1 / x .\)
4. \(f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+} \text {is defined by } f(x)=\sqrt{x+1}-1 \text { and } g: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+} \text {is defined by } g(x)=x^{2}+2 x \text {. }\)

Most functions do not have an inverse. In fact, only bijections have an inverse:

Theorem \(6.7.12\).

Suppose \(f: A \rightarrow B\). If \(f\) has an inverse \(f^{−1}: B \rightarrow A\), then \(f\) is a bijection.

Proof

Assume there is a function \(f^{−1}: B \rightarrow A\) that is an inverse of \(f\). Then

1. \(f^{-1}(f(a))=a \text { for all } a \in A\), and
2. \(f\left(f^{-1}(b)\right)=b \text { for all } b \in B\).

We wish to show that \(f\) is a bijection. This is left as an exercise for the reader. [Hint: This is very similar to many of the previous proofs that functions are bijections, but with the equation \(a = f^{−1}(b)\) in place of an explicit formula for \(a\). For example, if \(f(a_{1}) = f(a_{2})\), then \(f^{−1} (f(a_{1})) = f^{−1}(f(a_{2}))\). What is each side of this equation equal to?]

Exercise \(6.7.13\).

1. Prove that the inverse of a bijection is a bijection.
2. Prove the converse of Exercise \(6.7.3\).
3. Show that the inverse of a function is unique: if \(g_{1}\) and \(g_{2}\) are inverses of \(f\), then \(g_{1} = g_{2}\). (This is why we speak of the inverse of \(f\), rather than an inverse of \(f\).)

Remark \(6.7.14\).

If \(f\) is a function that has an inverse, then it is easy to find \(f^{−1}\) as a set of ordered pairs. Namely, \[f^{-1}=\{(b, a) \mid(a, b) \in f\} .\]

This is simply a restatement of the fact that \[b=f(a) \Leftrightarrow a=f^{-1}(b)\]

(or the fact that the arrow diagram of \(f^{−1}\) is obtained by reversing the arrows in the arrow diagram of \(f\)).

Exercise \(6.7.15\).

Prove the converse of Theorem \(6.7.12.\) [Hint: Find \(f^{−1}\) as a set of ordered pairs.]

Exercise \(6.7.16\).

Suppose \(f: A \rightarrow B\) is a bijection. Show that the inverse of \(f^{−1}\) is \(f\). That is, \((f^{−1})^{−1} = f\).