9.4: Fundamental Theorem of Algebra
- Page ID
- 99111
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Algebra over the complex numbers is in many ways easier than over the real numbers. The reason is that a polynomial of degree \(N\) in \(\mathbb{C}[z]\) has exactly \(N\) zeroes, counting multiplicity. This is called the Fundamental Theorem of Algebra. To prove it, we must establish some preliminary results.
Some Analysis.
DEFINITION. We say that a sequence \(\left\langle z_{n}=x_{n}+i y_{n}\right\rangle\) of complex numbers converges to the number \(z=x+i y\) iff \(\left\langle x_{n}\right\rangle\) converges to \(x\) and \(\left\langle y_{n}\right\rangle\) converges to \(y\). We say the sequence is Cauchy iff both \(\left\langle x_{n}\right\rangle\) and \(\left\langle y_{n}\right\rangle\) are Cauchy.
REMARK. This is the same as saying that \(\left\langle z_{n}\right\rangle\) converges to \(z\) iff \(\left|z-z_{n}\right|\) tends to zero, and that \(\left\langle z_{n}\right\rangle\) is Cauchy iff \[(\forall \varepsilon>0)(\exists N)(\forall m, n>N)\left|z_{m}-z_{n}\right|<\varepsilon .\] DEFINITION. Let \(G \subseteq \mathbb{C}\). We say a function \(f: G \rightarrow \mathbb{C}\) is continuous on \(G\) if, whenever \(\left\langle z_{n}\right\rangle\) is a sequence in \(G\) that converges to some value \(z_{\infty}\) in \(G\), then \(\left\langle f\left(z_{n}\right)\right\rangle\) converges to \(f\left(z_{\infty}\right)\).
PROPOSITION 9.34. Polynomials are continuous functions on \(\mathbb{C}\).
Proof. Repeat the proof of Proposition \(5.23\) with complex numbers instead of real numbers.
DEFINITION. A closed rectangle is a set of the form \(\{z \in \mathbb{C} \mid a \leq\) \(\Re(z) \leq b, c \leq \Im(z) \leq d\}\) for some real numbers \(a \leq b\) and \(c \leq d\). We would like a version of the Extreme Value Theorem, but it is not clear how the minimum and maximum values of a complex valued function should be defined. However, our definition of continuity makes sense even if the range of \(f\) is contained in \(\mathbb{R}\), and every complex valued continuous function \(g\) has three naturally associated real-valued continuous functions, viz. \(\Re(g), \Im(g)\) and \(|g|\).
THEOREM 9.35. Let \(R\) be a closed rectangle in \(\mathbb{C}\), and \(f: R \rightarrow \mathbb{R} a\) continuous function. Then \(f\) attains its maximum and its minimum.
Proof. Let \(R=\{z \in \mathbb{C} \mid a \leq \Re(z) \leq b, c \leq \Im(z) \leq d\}\). Let \(\left\langle z_{n}=x_{n}+i y_{n}\right\rangle\) be a sequence of points such that \(f\left(z_{n}\right)\) tends to either the least upper bound of the range of \(f\), if this exists, or let \(f\left(z_{n}\right)>n\) for all \(n\), if the range is not bounded above. By the BolzanoWeierstrass Theorem 8.6, there is some subsequence for which the real parts converge to some number \(x_{\infty}\) in \([a, b]\). By Bolzano-Weierstrass again, some subsequence of this subsequence has the property that the imaginary parts also converge, to some point \(y_{\infty}\) in \([c, d]\). So, replacing the original sequence by this subsequence of the subsequence, we can assume that \(z_{n}\) converges to the point \(z_{\infty}=x_{\infty}+i y_{\infty} \in R\). By continuity, \(f\left(z_{\infty}\right)=\lim _{n \rightarrow \infty} f\left(z_{n}\right)\). If the original sequence were unbounded then \(f\left(z_{n}\right)>n\) in the subsequence. This is impossible since the sequence \(\left\langle f\left(z_{n}\right)\right\rangle\) converges to \(f\left(z_{\infty}\right)\). Therefore the subsequence is bounded and \(f\left(z_{\infty}\right)\) must be the least upper bound of the range of \(f\). Therefore \(f\left(z_{\infty}\right)\) is the maximum of \(f\) over \(R\).
A similar argument shows that the minimum is also attained.
REMARK. The previous theorem can be improved to show that a continuous real-valued function on a closed bounded set in \(\mathbb{C}\) attains its extrema. A set \(F\) is closed if whenever a sequence of points \(\left\langle z_{n}\right\rangle\) converges to some complex number \(z_{\infty}\), then \(z_{\infty}\) is in \(F\). A set is bounded if it is contained in some rectangle.
We need one more geometric fact. LEMMA 9.36. Triangle inequality Let \(z_{1}, z_{2}\) be complex numbers. Then \[\left|z_{1}+z_{2}\right| \leq\left|z_{1}\right|+\left|z_{2}\right|\]
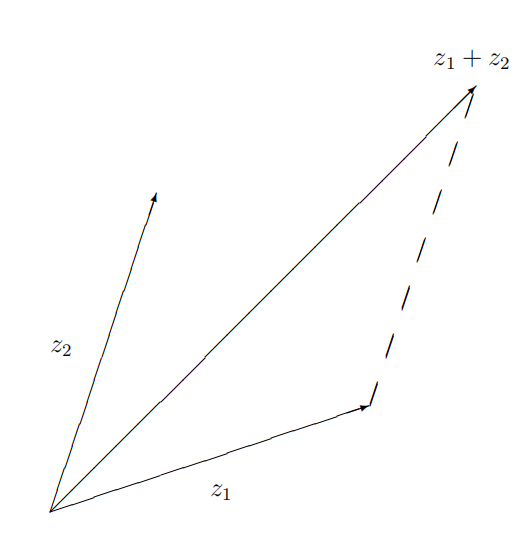
Proof. Write \(z_{1}=r_{1} \operatorname{Cis}\left(\theta_{1}\right)\) and \(z_{2}=r_{2} \operatorname{Cis}\left(\theta_{2}\right)\). Then \[\begin{aligned} \left|r_{1} \operatorname{Cis}\left(\theta_{1}\right)+r_{2} \operatorname{Cis}\left(\theta_{2}\right)\right| \\ &=\left[\left(r_{1} \cos \theta_{1}+r_{2} \cos \theta_{2}\right)^{2}+\left(r_{1} \sin \theta_{1}+r_{2} \operatorname{si}\right.\right.\\ &=\left[r_{1}^{2}+r_{2}^{2}+2 r_{1} r_{2}\left(\cos \theta_{1} \cos \theta_{2}+\sin \theta_{1} \sin \theta_{2}\right)\right] \\ &=\left[r_{1}^{2}+r_{2}^{2}+2 r_{1} r_{2} \cos \left(\theta_{1}-\theta_{2}\right)\right]^{1 / 2} \\ & \leq\left[r_{1}^{2}+r_{2}^{2}+2 r_{1} r_{2}\right]^{1 / 2} \\ &=r_{1}+r_{2} . \end{aligned}\] COROLLARY 9.38. Let \(z_{1}, \ldots, z_{n} \in \mathbb{C}\). Then \[\left|z_{1}+\cdots+z_{n}\right| \leq\left|z_{1}\right|+\cdots+\left|z_{n}\right| .\]
The Proof of the Fundamental Theorem of Algebra.
First we observe that finding roots and finding factors are closely related.
LEMMA 9.39. Let \(p\) be a polynomial of degree \(N \geq 1\) in \(\mathbb{C}[z]\). A complex number, \(c\), is a root of \(p\) iff \[p(z)=(z-c) q(z),\] where \(q\) is a polynomial of degree \(N-1\).
Proof. Repeat the proof of Lemma \(4.13\) with real numbers replaced by complex numbers.
Now we prove D’Alembert’s lemma, which states that the modulus of a polynomial cannot have a local minimum except at a root.
LEMMA 9.40. D’Alembert’s Lemma Let \(p \in \mathbb{C}[z]\) and \(\alpha \in \mathbb{C}\). If \(p(\alpha) \neq 0\), then \[(\forall \varepsilon>0)(\exists \zeta)[|\zeta-\alpha|<\varepsilon] \wedge[|p(\zeta)|<|p(\alpha)|]\] Proof. Fix \(\alpha\), not a root of \(p\). Write \(p\) as \[p(z)=\sum_{k=0}^{N} a_{k}(z-\alpha)^{k},\] where neither \(a_{0}\) nor \(a_{N}\) are 0 . Let \[m=\min \left\{j \in \mathbb{N}^{+} \mid a_{j} \neq 0\right\} .\] So \[p(z)=a_{0}+a_{m}(z-\alpha)^{m}+\cdots+a_{N}(z-\alpha)^{N} .\] Let \(a_{0}=r_{0} \operatorname{Cis}\left(\theta_{0}\right)\) and \(a_{m}=r_{m} \operatorname{Cis}\left(\theta_{m}\right)\). We will choose \(\zeta\) of the form \[\zeta=\alpha+\rho \operatorname{Cis}(\phi)\] in such a way as to get some cancellation in the first two terms of (9.42). So, let \[\phi=\frac{\theta_{0}+\pi-\theta_{m}}{m} .\] Then \[a_{0}+a_{m}(\zeta-\alpha)^{m}=r_{0} \operatorname{Cis}\left(\theta_{0}\right)-r_{m} \rho^{m} \operatorname{Cis}\left(\theta_{0}\right) .\] It remains to show that, for \(\rho\) small enough, we can ignore all the higher order terms. Note that if \(\rho<1\), we have \[\begin{aligned} \left|a_{m+1}(\zeta-\alpha)^{m+1}+\cdots+a_{N}(\zeta-\alpha)^{N}\right| \\ & \leq\left|a_{m+1}(\zeta-\alpha)^{m+1}\right|+\cdots+\left|a_{N}(\zeta-\alpha)^{N}\right| \\ &=\left|a_{m+1}\right| \rho^{m+1}+\cdots+\left|a_{N}\right| \rho^{N} \\ & \leq \rho^{m+1}\left[\left|a_{m+1}\right|+\cdots+\left|a_{N}\right|\right] \\ &=: C \rho^{m+1} . \end{aligned}\] Choose \(\rho\) so that \(r_{m} \rho^{m}<r_{0}\). Then \[p(\zeta)=\left(r_{0}-r_{m} \rho^{m}\right) \operatorname{Cis}\left(\theta_{0}\right)+a_{m+1}(\zeta-\alpha)^{m+1}+\cdots+a_{N}(\zeta-\alpha)^{N},\] \(\mathrm{SO}\) \[|p(\zeta)| \leq r_{0}-r_{m} \rho^{m}+C \rho^{m+1} .\] If \(\rho<r_{m} / C\), the right-hand side of (9.43) is smaller than \(r_{0}\).
So we conclude that by taking \[\rho=\frac{1}{2} \min \left(1, \frac{r_{m}}{C},\left[\frac{r_{0}}{r_{m}}\right]^{1 / m}, \varepsilon\right)\] then \[\zeta=\rho \operatorname{Cis}\left(\frac{\theta_{0}+\pi-\theta_{m}}{m}\right)\] satisfies the conclusion of the lemma.
THEOREM 9.44. Fundamental Theorem of Algebra Let \(p \in \mathbb{C}[z]\) be a polynomial of degree \(N \geq 1\). Then \(p\) can be factored as \[p(z)=c\left(z-\alpha_{1}\right) \ldots\left(z-\alpha_{N}\right)\] for complex numbers \(c, \alpha_{1}, \ldots, \alpha_{N}\). Moreover the factoring is unique up to order. Proof. (i) Show that \(p\) has at least one root.
Let \(p(z)=\sum_{k=0}^{N} a_{k} z^{k}\), with \(a_{N} \neq 0\). Let \(S\) be the closed square \(\{z \in \mathbb{C} \mid-L \leq \Re(z) \leq L,-L \leq \Im(z) \leq L\}\), where \(L\) is some (large) number to be chosen later.
If \(|z|=R\) then \[\left|\sum_{k=0}^{N-1} a_{k} z^{k}\right| \leq \sum_{k=0}^{N-1}\left|a_{k}\right| R^{k} .\] Choose \(L_{0}\) so that if \(R \geq L_{0}\), then \[\sum_{k=0}^{N-1}\left|a_{k}\right| R^{k} \leq \frac{1}{2}\left|a_{N}\right| R^{N} .\] Then if \(L \geq L_{0}\) and \(z\) is outside \(S\), we have \[\begin{aligned} \left|a_{N} z^{N}\right| &=\left|p(z)-\sum_{k=0}^{N-1} a_{k} z^{k}\right| \\ & \leq|p(z)|+\left|\sum_{k=0}^{N-1} a_{k} z^{k}\right| \\ & \leq|p(z)|+\frac{1}{2}\left|a_{N}\right| L^{N}, \end{aligned}\] where the first inequality is the triangle inequality, and the second because \(|z|>L\). Choose \(L_{1}\) such that \[\frac{1}{2}\left|a_{N}\right| L_{1}^{N}>\left|a_{0}\right| .\] Let \(L=\max \left(L_{0}, L_{1}\right)\), and let \(S\) be the corresponding closed square. The function \(|p|\) is continuous on \(S\), so it attains its minimum at some point, \(\alpha_{1}\) say, by Theorem 9.35. On the boundary of \(S\), we know \[|p(z)| \geq \frac{1}{2}\left|a_{N}\right| L^{N}>\left|a_{0}\right|=|p(0)| .\] Therefore \(\alpha_{1}\) must be in the interior of \(S\). By D’Alembert’s lemma, we must have \(p\left(\alpha_{1}\right)=0\), or else there would be a nearby point \(\zeta\), also in \(S\), where \(|p(\zeta)|\) was smaller than \(\left|p\left(\alpha_{1}\right)\right|\). So \(\alpha_{1}\) is a root of \(p\).
(ii) Now we apply Lemma \(9.39\) to conclude that we can factor \(p\) as \[p(z)=\left(z-\alpha_{1}\right) q(z)\] where \(q\) is a polynomial of degree \(N-1\). By a straightforward induction argument, we can factor \(p\) into \(N\) linear factors.
(iii) Uniqueness is obvious. The number \(c\) is the coefficient \(a_{N}\). The numbers \(a_{k}\) are precisely the points at which the function \(p\) vanishes, as it follows from Proposition \(9.19\) that the product of finitely many complex numbers can be 0 if and only if one of the numbers is itself 0 .


