1.8: Multiply Whole Numbers (Part 2)
- Page ID
- 5772
Translate Word Phrases to Math Notation
Earlier in this section, we translated math notation into words. Now we’ll reverse the process and translate word phrases into math notation. Some of the words that indicate multiplication are given in Table \(\PageIndex{3}\).
| Operation | Word Phrase | Example | Expression |
|---|---|---|---|
| Multiplication | times | 3 times 8 | 3 × 8, 3 • 8, (3)(8), |
| product | the product of 3 and 8 | (3)8, or 3(8) | |
| twice | twice 4 | 2 • 4 |
Translate and simplify: the product of \(12\) and \(27\).
Solution
The word product tells us to multiply. The words of \(12\) and \(27\) tell us the two factors.
| the product of 12 and 27 | |
| Translate. | 12 • 27 |
| Multiply. | 324 |
Translate and simplify the product of \(13\) and \(28\).
- Answer
-
\(13 · 28\); \(364\)
Translate and simplify the product of \(47\) and \(14\).
- Answer
-
\(47 · 14\); \(658\)
Translate and simplify: twice two hundred eleven.
Solution
The word twice tells us to multiply by \(2\).
| twice two hundred eleven | |
| Translate. | 2(211) |
| Multiply. | 422 |
Translate and simplify: twice one hundred sixty-seven.
- Answer
-
\(2(167)\); \(334\)
Translate and simplify: twice two hundred fifty-eight.
- Answer
-
\(2(258)\); \(516\)
Multiply Whole Numbers in Applications
We will use the same strategy we used previously to solve applications of multiplication. First, we need to determine what we are looking for. Then we write a phrase that gives the information to find it. We then translate the phrase into math notation and simplify to get the answer. Finally, we write a sentence to answer the question.
Humberto bought \(4\) sheets of stamps. Each sheet had \(20\) stamps. How many stamps did Humberto buy?
Solution
We are asked to find the total number of stamps.
| Write a phrase for the total. | the product of 4 and 20 |
| Translate to math notation. | 4 • 20 |
| Multiply. |  |
| Write a sentence to answer the question. | Humberto bought 80 stamps. |
Valia donated water for the snack bar at her son’s baseball game. She brought \(6\) cases of water bottles. Each case had \(24\) water bottles. How many water bottles did Valia donate?
- Answer
-
Valia donated \(144\) water bottles.
Vanessa brought \(8\) packs of hot dogs to a family reunion. Each pack has \(10\) hot dogs. How many hot dogs did Vanessa bring?
- Answer
-
Vanessa bought \(80\) hot dogs.
When Rena cooks rice, she uses twice as much water as rice. How much water does she need to cook \(4\) cups of rice?
Solution
We are asked to find how much water Rena needs.
| Write as a phrase. | twice as much as 4 cups |
| Translate to math notation. | 2 • 4 |
| Multiply to simplify. | 8 |
| Write a sentence to answer the question. | Rena needs 8 cups of water for cups of rice. |
Erin is planning her flower garden. She wants to plant twice as many dahlias as sunflowers. If she plants \(14\) sunflowers, how many dahlias does she need?
- Answer
-
Erin needs \(28\) dahlias.
A college choir has twice as many women as men. There are \(18\) men in the choir. How many women are in the choir?
- Answer
-
There are \(36\) women in the choir.
Van is planning to build a patio. He will have \(8\) rows of tiles, with \(14\) tiles in each row. How many tiles does he need for the patio?
Solution
We are asked to find the total number of tiles.
| Write as a phrase. | the product of 8 and 14 |
| Translate to math notation. | 8 • 14 |
| Multiply to simplify. | 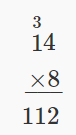 |
| Write a sentence to answer the question. | Van needs 112 tiles for his patio. |
Jane is tiling her living room floor. She will need \(16\) rows of tile, with \(20\) tiles in each row. How many tiles does she need for the living room floor?
- Answer
-
Jane needs \(320\) tiles.
Yousef is putting shingles on his garage roof. He will need \(24\) rows of shingles, with \(45\) shingles in each row. How many shingles does he need for the garage roof?
- Answer
-
Yousef needs \(1,080\) tiles.
If we want to know the size of a wall that needs to be painted or a floor that needs to be carpeted, we will need to find its area. The area is a measure of the amount of surface that is covered by the shape. Area is measured in square units. We often use square inches, square feet, square centimeters, or square miles to measure area. A square centimeter is a square that is one centimeter (cm.) on a side. A square inch is a square that is one inch on each side, and so on.
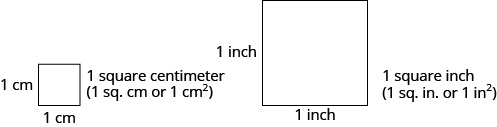
Figure \(\PageIndex{2}\)
For a rectangular figure, the area is the product of the length and the width. Figure \(\PageIndex{3}\) shows a rectangular rug with a length of \(2\) feet and a width of \(3\) feet. Each square is \(1\) foot wide by \(1\) foot long, or \(1\) square foot. The rug is made of \(6\) squares. The area of the rug is \(6\) square feet.
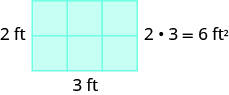
Figure \(\PageIndex{3}\): The area of a rectangle is the product of its length and its width, or 6 square feet.
Jen’s kitchen ceiling is a rectangle that measures \(9\) feet long by \(12\) feet wide. What is the area of Jen’s kitchen ceiling?
Solution
We are asked to find the area of the kitchen ceiling.
| Write as a phrase. | the product of 9 and 12 |
| Translate to math notation. | 9 • 12 |
| Multiply to simplify. | 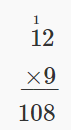 |
| Write a sentence to answer the question. | The area of Jen's kitchen ceiling is 108 square feet. |
Zoila bought a rectangular rug. The rug is \(8\) feet long by \(5\) feet wide. What is the area of the rug?
- Answer
-
The area of the rug is \(40\) square feet.
Rene’s driveway is a rectangle \(45\) feet long by \(20\) feet wide. What is the area of the driveway?
- Answer
-
The area of the driveway is \(900\) square feet
Access Additional Online Resources
Key Concepts
| Operation | Notation | Expression | Read as | Result |
|---|---|---|---|---|
- Multiplication Property of Zero
- The product of any number and \(0\) is \(0\).
- The product of any number and \(0\) is \(0\).
- Identity Property of Multiplication
- The product of any number and \(1\) is the number.
- The product of any number and \(1\) is the number.
- Commutative Property of Multiplication
- Changing the order of the factors does not change their product.
- Changing the order of the factors does not change their product.
- Multiply two whole numbers to find the product.
- Write the numbers so each place value lines up vertically.
- Multiply the digits in each place value.
- Work from right to left, starting with the ones place in the bottom number.
- Multiply the bottom number by the ones digit in the top number, then by the tens digit, and so on.
- If a product in a place value is more than \(9\), carry to the next place value.
- Write the partial products, lining up the digits in the place values with the numbers above. Repeat for the tens place in the bottom number, the hundreds place, and so on.
- Insert a zero as a placeholder with each additional partial product.
- Add the partial products.
Glossary
- product
-
The product is the result of multiplying two or more numbers.
Practice Makes Perfect
Use Multiplication Notation
In the following exercises, translate from math notation to words.
- 4 × 7
- 8 × 6
- 5 • 12
- 3 • 9
- (10)(25)
- (20)(15)
- 42(33)
- 39(64)
Model Multiplication of Whole Numbers
In the following exercises, model the multiplication.
- 3 × 6
- 4 × 5
- 5 × 9
- 3 × 9
Multiply Whole Numbers
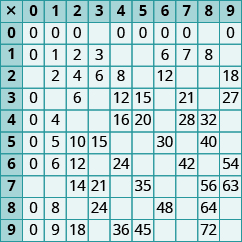
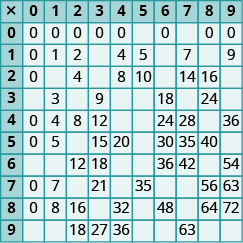
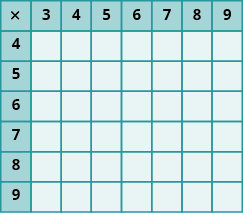
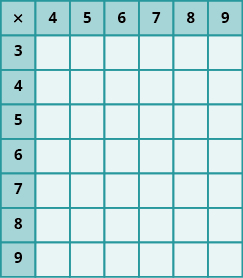
In the following exercises, fill in the missing values in each chart.
In the following exercises, multiply.
- 0 • 15
- 0 • 41
- (99)0
- (77)0
- 1 • 43
- 1 • 34
- (28)1
- (65)1
- 1(240,055)
- 1(189,206)
- (a) 7 • 6 (b) 6 • 7
- (a) 8 × 9 (b) 9 × 8
- (79)(5)
- (58)(4)
- 275 • 6
- 638 • 5
- 3,421 × 7
- 9,143 × 3
- 52(38)
- 37(45)
- 96 • 73
- 89 • 56
- 27 × 85
- 53 × 98
- 23 • 10
- 19 • 10
- (100)(36)
- (100)(25)
- 1,000(88)
- 1,000(46)
- 50 × 1,000,000
- 30 × 1,000,000
- 247 × 139
- 156 × 328
- 586(721)
- 472(855)
- 915 • 879
- 968 • 926
- (104)(256)
- (103)(497)
- 348(705)
- 485(602)
- 2,719 × 543
- 3,581 × 724
Translate Word Phrases to Math Notation
In the following exercises, translate and simplify.
- the product of 18 and 33
- the product of 15 and 22
- fifty-one times sixty-seven
- forty-eight times seventy-one
- twice 249
- twice 589
- ten times three hundred seventy-five
- ten times two hundred fifty-five
Mixed Practice
In the following exercises, simplify.
- 38 × 37
- 86 × 29
- 415 − 267
- 341 − 285
- 6,251 + 4,749
- 3,816 + 8,184
- (56)(204)
- (77)(801)
- 947 • 0
- 947 + 0
- 15,382 + 1
- 15,382 • 1
In the following exercises, translate and simplify.
- the difference of 50 and 18
- the difference of 90 and 66
- twice 35
- twice 140
- 20 more than 980
- 65 more than 325
- the product of 12 and 875
- the product of 15 and 905
- subtract 74 from 89
- subtract 45 from 99
- the sum of 3,075 and 950
- the sum of 6,308 and 724
- 366 less than 814
- 388 less than 925
Multiply Whole Numbers in Applications
In the following exercises, solve.
- Party supplies Tim brought 9 six-packs of soda to a club party. How many cans of soda did Tim bring?
- Sewing Kanisha is making a quilt. She bought 6 cards of buttons. Each card had four buttons on it. How many buttons did Kanisha buy?
- Field trip Seven school busses let off their students in front of a museum in Washington, DC. Each school bus had 44 students. How many students were there?
- Gardening Kathryn bought 8 flats of impatiens for her flower bed. Each flat has 24 flowers. How many flowers did Kathryn buy?
- Charity Rey donated 15 twelve-packs of t-shirts to a homeless shelter. How many t-shirts did he donate?
- School There are 28 classrooms at Anna C. Scott elementary school. Each classroom has 26 student desks. What is the total number of student desks?
- Recipe Stephanie is making punch for a party. The recipe calls for twice as much fruit juice as club soda. If she uses 10 cups of club soda, how much fruit juice should she use?
- Gardening Hiroko is putting in a vegetable garden. He wants to have twice as many lettuce plants as tomato plants. If he buys 12 tomato plants, how many lettuce plants should he get?
- Government The United States Senate has twice as many senators as there are states in the United States. There are 50 states. How many senators are there in the United States Senate?
- Recipe Andrea is making potato salad for a buffet luncheon. The recipe says the number of servings of potato salad will be twice the number of pounds of potatoes. If she buys 30 pounds of potatoes, how many servings of potato salad will there be?
- Painting Jane is painting one wall of her living room. The wall is rectangular, 13 feet wide by 9 feet high. What is the area of the wall?
- Home décor Shawnte bought a rug for the hall of her apartment. The rug is 3 feet wide by 18 feet long. What is the area of the rug?
- Room size The meeting room in a senior center is rectangular, with length 42 feet and width 34 feet. What is the area of the meeting room?
- Gardening June has a vegetable garden in her yard. The garden is rectangular, with length 23 feet and width 28 feet. What is the area of the garden?
- NCAA basketball According to NCAA regulations, the dimensions of a rectangular basketball court must be 94 feet by 50 feet. What is the area of the basketball court?
- NCAA football According to NCAA regulations, the dimensions of a rectangular football field must be 360 feet by 160 feet. What is the area of the football field?
Everyday Math
- Stock market Javier owns 300 shares of stock in one company. On Tuesday, the stock price rose $12 per share. How much money did Javier’s portfolio gain?
- Salary Carlton got a $200 raise in each paycheck. He gets paid 24 times a year. How much higher is his new annual salary?
Writing Exercises
- How confident do you feel about your knowledge of the multiplication facts? If you are not fully confident, what will you do to improve your skills?
- How have you used models to help you learn the multiplication facts?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.