10.S: Polynomials (Summary)
- Page ID
- 7277
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Key Terms
| binomial | A polynomial with exactly two terms |
| degree of a constant | The degree of a constant is 0. |
| degree of a polynomial | The degree of a polynomial is the highest degree of all its terms. |
| degree of a term | The degree of a term of a polynomial is the exponent of its variable. |
| greatest common factor | The greatest common factor (GCF) of two or more expressions is the largest expression that is a factor of all the expressions. |
| monomial | A term of the form axm, where a is a constant and m is a whole number, is called a monomial. |
| negative exponent | If n is a positive integer and a ≠ 0, then \(a^{-n} = \dfrac{1}{a^{n}}\). |
| polynomial | A polynomial is a monomial, or two or more monomials, combined by addition or subtraction. |
| scientific notation | A number expressed in scientific notation when it is of the form a × 10n, where a ≥ 1 and a < 10, and n is an integer. |
| trinomial | A trinomial is a polynomial with exactly three terms. |
| zero exponent | If a is a non-zero number, then a0 = 1. Any nonzero number raised to the zero power is 1. |
Key Concepts
10.2 - Use Multiplication Properties of Exponents
- Exponential Notation
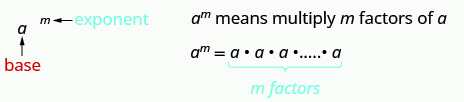
This is read a to the mth power.
- Product Property of Exponents
- If a is a real number and m, n are counting numbers, then am • an = am + n
- To multiply with like bases, add the exponents.
- Power Property for Exponents
- If a is a real number and m, n are counting numbers, then (am)n = am • n
- Product to a Power Property for Exponents
- If a and b are real numbers and m is a whole number, then (ab)m = ambm
10.3 - Multiply Polynomials
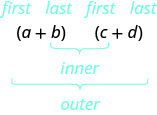
• Use the FOIL method for multiplying two binomials.
| Step 1. Multiply the First terms. |
|
| Step 2. Multiply the Outer terms. | |
| Step 3. Multiply the Inner terms. | |
| Step 4. Multiply the Last terms. | |
| Step 5. Combine like terms, when possible. |
- Multiplying Two Binomials: To multiply binomials, use the:
- Distributive Property
- FOIL Method
- Vertical Method
- Multiplying a Trinomial by a Binomial: To multiply a trinomial by a binomial, use the:
- Distributive Property
- Vertical Method
10.4 - Divide Monomials
- Equivalent Fractions Property
- If a, b, c are whole numbers where b ≠ 0, c ≠ 0, then$$\dfrac{a}{b} = \dfrac{a \cdot c}{b \cdot c} \quad and \quad \dfrac{a \cdot c}{b \cdot c} = \dfrac{a}{b}$$
- Zero Exponent
- If a is a non-zero number, then a0 = 1.
- Any nonzero number raised to the zero power is 1.
- Quotient Property for Exponents
- If a is a real number, a ≠ 0, and m, n are whole numbers, then$$\dfrac{a^{m}}{a^{n}} = a^{m-n},\; m>n \quad and \quad \dfrac{a^{m}}{a^{n}} = \dfrac{1}{a^{n-m}},\; n>m$$
- Quotient to a Power Property for Exponents
- If a and b are real numbers, b ≠ 0, and m is a counting number, then$$\left(\dfrac{a}{b}\right)^{m} = \dfrac{a^{m}}{b^{m}}$$
- To raise a fraction to a power, raise the numerator and denominator to that power.
10.5 - Integer Exponents and Scientific Notation
- Summary of Exponent Properties
- If a, b are real numbers and m, n are integers, then
| Product Property | am • an = am + n |
| Power Property | (am)n = am • n |
| Product to a Power Property | (ab)m = ambm |
| Quotient Property | \(\dfrac{a^{m}}{a^{n}}\) = am − n, a ≠ 0, m > n |
| \(\dfrac{a^{m}}{a^{n}} = \dfrac{1}{a^{n-m}}\), a ≠ 0, n > m | |
| Zero Exponent Property | a0 = 1, a ≠ 0 |
| Quotient to a Power Property | \(\left(\dfrac{a}{b}\right)^{m} = \dfrac{a^{m}}{b^{m}}\), b ≠ 0 |
| Definition of a Negative Exponent | \(a^{-n} = \dfrac{1}{a^{n}}\) |
- Convert from Decimal Notation to Scientific Notation: To convert a decimal to scientific notation:
- Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
- Count the number of decimal places, n, that the decimal point was moved. Write the number as a product with a power of 10.
- If the original number is greater than 1, the power of 10 will be 10n.
- If the original number is between 0 and 1, the power of 10 will be 10n.
- Check.
- Convert Scientific Notation to Decimal Form: To convert scientific notation to decimal form:
- Determine the exponent, n, on the factor 10.
- Move the decimal n places, adding zeros if needed.
- If the exponent is positive, move the decimal point n places to the right.
- If the exponent is negative, move the decimal point |n| places to the left.
- Check.
10.6 - Introduction to Factoring Polynomials
- Find the greatest common factor.
- Factor each coefficient into primes. Write all variables with exponents in expanded form.
- List all factors—matching common factors in a column. In each column, circle the common factors.
- Bring down the common factors that all expressions share.
- Multiply the factors.
- Distributive Property
- If a , b , c are real numbers, then a(b + c) = ab + ac and ab + ac = a(b + c).
- Factor the greatest common factor from a polynomial.
- Find the GCF of all the terms of the polynomial.
- Rewrite each term as a product using the GCF.
- Use the Distributive Property ‘in reverse’ to factor the expression.
- Check by multiplying the factors.
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."