10.S: Polynomials (Summary)

Last updated
Save as PDF

Page ID: 7277

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Key Terms

binomial	A polynomial with exactly two terms
degree of a constant	The degree of a constant is 0.
degree of a polynomial	The degree of a polynomial is the highest degree of all its terms.
degree of a term	The degree of a term of a polynomial is the exponent of its variable.
greatest common factor	The greatest common factor (GCF) of two or more expressions is the largest expression that is a factor of all the expressions.
monomial	A term of the form ax^m, where a is a constant and m is a whole number, is called a monomial.
negative exponent	If n is a positive integer and a ≠ 0, then $a^{-n} = \dfrac{1}{a^{n}}$.
polynomial	A polynomial is a monomial, or two or more monomials, combined by addition or subtraction.
scientific notation	A number expressed in scientific notation when it is of the form a × 10ⁿ, where a ≥ 1 and a < 10, and n is an integer.
trinomial	A trinomial is a polynomial with exactly three terms.
zero exponent	If a is a non-zero number, then a⁰ = 1. Any nonzero number raised to the zero power is 1.

Key Concepts

10.2 - Use Multiplication Properties of Exponents

Exponential Notation

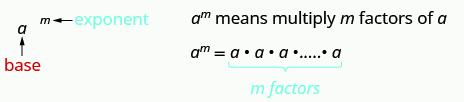
$On the left side, a raised to the m is shown. The m is labeled in blue as an exponent. The a is labeled in red as the base. On the right, it says a to the m means multiply m factors of a. Below this, it says a to the m equals a times a times a times a, with m factors written below in blue.$

This is read a to the m^thpower.

Product Property of Exponents
- If a is a real number and m, n are counting numbers, then a^m • aⁿ = a^{m + n}
- To multiply with like bases, add the exponents.
Power Property for Exponents
- If a is a real number and m, n are counting numbers, then (a^m)ⁿ = a^{m • n}
Product to a Power Property for Exponents
- If a and b are real numbers and m is a whole number, then (ab)^m = a^mb^m

10.3 - Multiply Polynomials

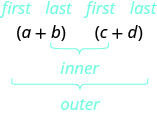
• Use the FOIL method for multiplying two binomials.

Step 1. Multiply the First terms.	$Parentheses a plus b times parentheses c plus d is shown. Above a is first, above b is last, above c is first, above d is last. There is a brace connecting a and d that says outer. There is a brace connecting b and c that says inner.$
Step 2. Multiply the Outer terms.
Step 3. Multiply the Inner terms.
Step 4. Multiply the Last terms.
Step 5. Combine like terms, when possible.

Multiplying Two Binomials: To multiply binomials, use the:
- Distributive Property
- FOIL Method
- Vertical Method
Multiplying a Trinomial by a Binomial: To multiply a trinomial by a binomial, use the:
- Distributive Property
- Vertical Method

10.4 - Divide Monomials

Equivalent Fractions Property
- If a, b, c are whole numbers where b ≠ 0, c ≠ 0, then$$\dfrac{a}{b} = \dfrac{a \cdot c}{b \cdot c} \quad and \quad \dfrac{a \cdot c}{b \cdot c} = \dfrac{a}{b}$$
Zero Exponent
- If a is a non-zero number, then a⁰ = 1.
- Any nonzero number raised to the zero power is 1.
Quotient Property for Exponents
- If a is a real number, a ≠ 0, and m, n are whole numbers, then$$\dfrac{a^{m}}{a^{n}} = a^{m-n},\; m>n \quad and \quad \dfrac{a^{m}}{a^{n}} = \dfrac{1}{a^{n-m}},\; n>m$$
Quotient to a Power Property for Exponents
- If a and b are real numbers, b ≠ 0, and m is a counting number, then$$\left(\dfrac{a}{b}\right)^{m} = \dfrac{a^{m}}{b^{m}}$$
- To raise a fraction to a power, raise the numerator and denominator to that power.

10.5 - Integer Exponents and Scientific Notation

Summary of Exponent Properties
- If a, b are real numbers and m, n are integers, then

Product Property	a^m • aⁿ = a^{m + n}
Power Property	(a^m)ⁿ = a^{m • n}
Product to a Power Property	(ab)^m = a^mb^m
Quotient Property	$\dfrac{a^{m}}{a^{n}}$ = a^{m − n}, a ≠ 0, m > n
	$\dfrac{a^{m}}{a^{n}} = \dfrac{1}{a^{n-m}}$, a ≠ 0, n > m
Zero Exponent Property	a⁰ = 1, a ≠ 0
Quotient to a Power Property	$\left(\dfrac{a}{b}\right)^{m} = \dfrac{a^{m}}{b^{m}}$, b ≠ 0
Definition of a Negative Exponent	$a^{-n} = \dfrac{1}{a^{n}}$

Convert from Decimal Notation to Scientific Notation: To convert a decimal to scientific notation:
1. Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
2. Count the number of decimal places, n, that the decimal point was moved. Write the number as a product with a power of 10.
  - If the original number is greater than 1, the power of 10 will be 10ⁿ.
  - If the original number is between 0 and 1, the power of 10 will be 10ⁿ.
3. Check.
Convert Scientific Notation to Decimal Form: To convert scientific notation to decimal form:
1. Determine the exponent, n, on the factor 10.
2. Move the decimal n places, adding zeros if needed.
  - If the exponent is positive, move the decimal point n places to the right.
  - If the exponent is negative, move the decimal point |n| places to the left.
3. Check.

10.6 - Introduction to Factoring Polynomials

Find the greatest common factor.
1. Factor each coefficient into primes. Write all variables with exponents in expanded form.
2. List all factors—matching common factors in a column. In each column, circle the common factors.
3. Bring down the common factors that all expressions share.
4. Multiply the factors.
Distributive Property
- If a , b , c are real numbers, then a(b + c) = ab + ac and ab + ac = a(b + c).
Factor the greatest common factor from a polynomial.
1. Find the GCF of all the terms of the polynomial.
2. Rewrite each term as a product using the GCF.
3. Use the Distributive Property ‘in reverse’ to factor the expression.
4. Check by multiplying the factors.

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."

Search

Text Color

Text Size

Margin Size

Font Type