10.1: Add and Subtract Polynomials

Learning Objectives

• Identify polynomials, monomials, binomials, and trinomials
• Determine the degree of polynomials
• Add and subtract monomials
• Add and subtract polynomials
• Evaluate a polynomial for a given value

be prepared!

Before you get started, take this readiness quiz.

1. Simplify: 8x + 3x. If you missed this problem, review Example 2.3.10.
2. Subtract: (5n + 8) − (2n − 1). If you missed this problem, review Example 7.4.13.
3. Evaluate: 4y² when y = 5 If you missed this problem, review Example 2.3.6.

Identify Polynomials, Monomials, Binomials, and Trinomials

In Evaluate, Simplify, and Translate Expressions, you learned that a term is a constant or the product of a constant and one or more variables. When it is of the form ax^m, where a is a constant and m is a whole number, it is called a monomial. A monomial, or a sum and/or difference of monomials, is called a polynomial.

Definition: Polynomials

polynomial — A monomial, or two or more monomials, combined by addition or subtraction

monomial — A polynomial with exactly one term

binomial — A polynomial with exactly two terms

trinomial — A polynomial with exactly three terms

Notice the roots:

• poly- means many
• mono- means one
• bi- means two
• tri- means three

Here are some examples of polynomials:

Polynomial	b + 1	4y^2 − 7y + 2	5x^5 − 4x^4 + x^3 + 8x^2 − 9x + 1
Monomial	5	4b^2	-9x^3
Binomial	3a - 7	y^2 - 9	17x^3 + 14x^2
Trinomial	x^2 - 5x + 6	4y^2 - 7y + 2	5a^4 - 3a^3 + a

Notice that every monomial, binomial, and trinomial is also a polynomial. They are special members of the family of polynomials and so they have special names. We use the words ‘monomial’, ‘binomial’, and ‘trinomial’ when referring to these special polynomials and just call all the rest ‘polynomials’.

Example $\PageIndex{1}$:

Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial: (a) 8x² − 7x − 9 (b) −5a⁴ (c) x⁴ − 7x³ − 6x² + 5x + 2 (d) 11 − 4y³ (e) n

Solution

Polynomial	Number of terms	Type
(a) 8x^2 − 7x − 9	3	Trinomial
(b) −5a^4	1	Monomial
(c) x^4 − 7x^3 − 6x^2 + 5x + 2	5	Polynomial
(d) 11 − 4y^3	2	Binomial
(e) n	1	Monomial

Exercise $\PageIndex{1}$:

Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial. (a) z (b) 2x³ − 4x² − x − 8 (c) 6x² − 4x + 1 (d) 9 − 4y² (e) 3x⁷

Answer a

monomial

Answer b

polynomial

Answer c

trinomial

Answer d

binomial

Answer e

monomial

Exercise $\PageIndex{2}$:

Determine whether each polynomial is a monomial, binomial, trinomial, or other polynomial. (a) y³ − 8 (b) 9x³ − 5x² − x (c) x⁴ − 3x² − 4x − 7 (d) −y⁴ (e) w

Answer a

binomial

Answer b

trinomial

Answer c

polynomial

Answer d

monomial

Answer e

monomial

Determine the Degree of Polynomials

In this section, we will work with polynomials that have only one variable in each term. The degree of a polynomial and the degree of its terms are determined by the exponents of the variable.

A monomial that has no variable, just a constant, is a special case. The degree of a constant is 0 —it has no variable.

Definition: Degree of a Polynomial

The degree of a term is the exponent of its variable.

The degree of a constant is 0.

The degree of a polynomial is the highest degree of all its terms.

Let's see how this works by looking at several polynomials. We'll take it step by step, starting with monomials, and then progressing to polynomials with more terms.

Remember: Any base written without an exponent has an implied exponent of 1.

Example $\PageIndex{2}$:

Find the degree of the following polynomials: (a) 4x (b) 3x³ − 5x + 7 (c) −11 (d) −6x² + 9x − 3 (e) 8x + 2

Solution

(a) 4x

The exponent of x is one. x = x^1

The degree is 1.

(b) 3x³ − 5x + 7

The highest degree of all the terms is 3.

The degree is 3.

(c) −11

The degree of a constant is 0.

The degree is 0.

(d) −6x² + 9x − 3

The highest degree of all the terms is 2.

The degree is 2.

(e) 8x + 2

The highest degree of all the terms is 1.

The degree is 1.

Exercise $\PageIndex{3}$:

Find the degree of the following polynomials: (a) −6y (b) 4x − 1 (c) 3x⁴ + 4x² − 8 (d) 2y² + 3y + 9 (e) −18

Answer a

1

Answer b

1

Answer c

4

Answer d

2

Answer e

0

Exercise $\PageIndex{4}$:

Find the degree of the following polynomials: (a) 47 (b) 2x² − 8x + 2 (c) x⁴ − 16 (d) y⁵ − 5y³ + y (e) 9a³

Answer a

0

Answer b

2

Answer c

4

Answer d

5

Answer e

3

Working with polynomials is easier when you list the terms in descending order of degrees. When a polynomial is written this way, it is said to be in standard form. Look back at the polynomials in Example 10.2. Notice that they are all written in standard form. Get in the habit of writing the term with the highest degree first.

Add and Subtract Monomials

In The Language of Algebra, you simplified expressions by combining like terms. Adding and subtracting monomials is the same as combining like terms. Like terms must have the same variable with the same exponent. Recall that when combining like terms only the coefficients are combined, never the exponents.

Example $\PageIndex{3}$:

Add: 17x² + 6x².

Solution

Combine like terms.

23x^2

Exercise $\PageIndex{5}$:

Add: 12x² + 5x².

Answer

17x²

Exercise $\PageIndex{6}$:

Add: −11y² + 8y².

Answer

-3y²

Example $\PageIndex{4}$:

Subtract: 11n − (−8n).

Solution

Combine like terms.

19n

Exercise $\PageIndex{7}$:

Subtract: 9n − (−5n).

Answer

14n

Exercise $\PageIndex{8}$:

Subtract: −7a³ − (−5a³).

Answer

-2a³

Example $\PageIndex{5}$:

Simplify: a² + 4b² − 7a².

Solution

Combine like terms.

−6a^2 + 4b^2

Remember, −6a² and 4b² are not like terms. The variables are not the same.

Exercise $\PageIndex{9}$:

Add: 3x² + 3y² − 5x².

Answer

-2x² + 3y²

Exercise $\PageIndex{10}$:

Add: 2a² + b² − 4a².

Answer

-2a² + b²

Add and Subtract Polynomials

Adding and subtracting polynomials can be thought of as just adding and subtracting like terms. Look for like terms—those with the same variables with the same exponent. The Commutative Property allows us to rearrange the terms to put like terms together. It may also be helpful to underline, circle, or box like terms.

Example $\PageIndex{6}$:

Find the sum: (4x² − 5x + 1) + (3x² − 8x − 9)

Solution

Identify like terms.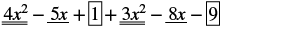
Rearrange to get the like terms together.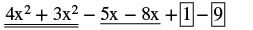
Combine like terms.

Exercise $\PageIndex{11}$:

Find the sum: (3x² − 2x + 8) + (x² − 6x + 2).

Answer

4x² - 8x + 10

Exercise $\PageIndex{12}$:

Find the sum: (7y² + 4y − 6) + (4y² + 5y + 1)

Answer

11y² + 9y - 5

Parentheses are grouping symbols. When we add polynomials as we did in Example 10.6, we can rewrite the expression without parentheses and then combine like terms. But when we subtract polynomials, we must be very careful with the signs.

Example $\PageIndex{7}$:

Find the difference: (7u² − 5u + 3) − (4u² − 2).

Solution

Distribute and identify like terms.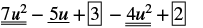
Rearrange the terms.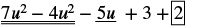
Combine like terms.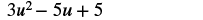

Exercise $\PageIndex{13}$:

Find the difference: (6y² + 3y − 1) − (3y² − 4).

Answer

3y² + 3y + 3

Exercise $\PageIndex{14}$:

Find the difference: (8u² − 7u − 2) − (5u² − 6u − 4).

Answer

3u² - u + 2

Example $\PageIndex{8}$:

Subtract: (m² − 3m + 8) from (9m² − 7m + 4).

Solution

Distribute and identify like terms.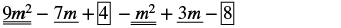
Rearrange the terms.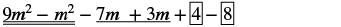
Combine like terms.

Exercise $\PageIndex{15}$:

Subtract: (4n² − 7n − 3) from (8n² + 5n − 3).

Answer

4n² + 12n

Exercise $\PageIndex{16}$:

Subtract: (a² − 4a − 9) from (6a² + 4a − 1).

Answer

5a² + 8a + 8

Evaluate a Polynomial for a Given Value

In The Language of Algebra we evaluated expressions. Since polynomials are expressions, we'll follow the same procedures to evaluate polynomials—substitute the given value for the variable into the polynomial, and then simplify.

Example $\PageIndex{9}$:

Evaluate 3x 2 − 9x + 7 when (a) x = 3 (b) x = −1

Solution

(a) x = 3

Substitute 3 for x.	3(3)^2 − 9(3) + 7
Simplify the expression with the exponent.	3 • 9 − 9(3) + 7
Multiply.	27 − 27 + 7
Simplify.	7

(b) x = −1

Substitute -1 for x.	3(-1)^2 − 9(-1) + 7
Simplify the expression with the exponent.	3 • 1 − 9(-1) + 7
Multiply.	3 + 9 + 7
Simplify.	19

Exercise $\PageIndex{17}$:

Evaluate: 2x² + 4x − 3 when (a) x = 2 (b) x = −3

Answer a

13

Answer b

3

Exercise $\PageIndex{18}$:

Evaluate: 7y² − y − 2 when (a) y = −4 (b) y = 0

Answer a

114

Answer b

-2

Example $\PageIndex{10}$:

The polynomial −16t 2 + 300 gives the height of an object t seconds after it is dropped from a 300 foot tall bridge. Find the height after t = 3 seconds.

Solution

Substitute 3 for t.	-16(3)^2 + 300
Simplify the expression with the exponent.	-16 • 9 + 300
Multiply.	-144 + 300
Simplify.	156

Exercise $\PageIndex{19}$:

The polynomial −8t² + 24t + 4 gives the height, in feet, of a ball t seconds after it is tossed into the air, from an initial height of 4 feet. Find the height after t = 3 seconds.

Answer

4 feet

Exercise $\PageIndex{20}$:

The polynomial −8t² + 24t + 4 gives the height, in feet, of a ball x seconds after it is tossed into the air, from an initial height of 4 feet. Find the height after t = 2 seconds.

Answer

20 feet

ACCESS ADDITIONAL ONLINE RESOURCES

Adding Polynomials

Subtracting Polynomials

Practice Makes Perfect

Identify Polynomials, Monomials, Binomials and Trinomials

In the following exercises, determine if each of the polynomials is a monomial, binomial, trinomial, or other polynomial.

1. 5x + 2
2. z² − 5z − 6
3. a² + 9a + 18
4. −12p⁴
5. y³ − 8y² + 2y − 16
6. 10 − 9x
7. 23y²
8. m⁴ + 4m³ + 6m² + 4m + 1

Determine the Degree of Polynomials

In the following exercises, determine the degree of each polynomial.

9. 8a⁵ − 2a³ + 1
10. 5c³ + 11c² − c − 8
11. 3x − 12
12. 4y + 17
13. −13
14. −22

Add and Subtract Monomials

In the following exercises, add or subtract the monomials.

15. 6x² + 9x²
16. 4y³ + 6y³
17. −12u + 4u
18. −3m + 9m
19. 5a + 7b
20. 8y + 6z
21. Add: 4a, − 3b, − 8a
22. Add: 4x, 3y, − 3x
23. 18x − 2x
24. 13a − 3a
25. Subtract 5x⁶ from − 12x⁶
26. Subtract 2p⁴ from − 7p⁴

Add and Subtract Polynomials

In the following exercises, add or subtract the polynomials.

27. (4y² + 10y + 3) + (8y² − 6y + 5)
28. (7x² − 9x + 2) + (6x² − 4x + 3)
29. (x² + 6x + 8) + (−4x² + 11x − 9)
30. (y² + 9y + 4) + (−2y² − 5y − 1)
31. (3a² + 7) + (a² − 7a − 18)
32. (p² − 5p − 11) + (3p² + 9)
33. (6m² − 9m − 3) − (2m² + m − 5)
34. (3n² − 4n + 1) − (4n² − n − 2)
35. (z² + 8z + 9) − (z² − 3z + 1)
36. (z² − 7z + 5) − (z² − 8z + 6)
37. (12s² − 15s) − (s − 9)
38. (10r² − 20r) − (r − 8)
39. Find the sum of (2p³ − 8) and (p² + 9p + 18)
40. Find the sum of (q² + 4q + 13) and (7q³ − 3)
41. Subtract (7x² − 4x + 2) from (8x² − x + 6)
42. Subtract (5x² − x + 12) from (9x² − 6x − 20)
43. Find the difference of (w² + w − 42) and (w² − 10w + 24)
44. Find the difference of (z² − 3z − 18) and (z² + 5z − 20)

Evaluate a Polynomial for a Given Value

In the following exercises, evaluate each polynomial for the given value.

45. Evaluate 8y² − 3y + 2
    1. y = 5
    2. y = −2
    3. y = 0
46. Evaluate 5y² − y − 7 when:
    1. y = −4
    2. y = 1
    3. y = 0
47. Evaluate 4 − 36x when:
    1. x = 3
    2. x = 0
    3. x = −1
48. Evaluate 16 − 36x² when:
    1. x = −1
    2. x = 0
    3. x = 2
49. A window washer drops a squeegee from a platform 275 feet high. The polynomial −16t² + 275 gives the height of the squeegee t seconds after it was dropped. Find the height after t = 4 seconds.
50. A manufacturer of microwave ovens has found that the revenue received from selling microwaves at a cost of p dollars each is given by the polynomial −5p² + 350p. Find the revenue received when p = 50 dollars.

Everyday Math

51. Fuel Efficiency The fuel efficiency (in miles per gallon) of a bus going at a speed of x miles per hour is given by the polynomial $− \dfrac{1}{160} x^{2} + \dfrac{1}{2} x$. Find the fuel efficiency when x = 40 mph.
52. Stopping Distance The number of feet it takes for a car traveling at x miles per hour to stop on dry, level concrete is given by the polynomial 0.06x² + 1.1x. Find the stopping distance when x = 60 mph.

Writing Exercises

53. Using your own words, explain the difference between a monomial, a binomial, and a trinomial.
54. Eloise thinks the sum 5x² + 3x⁴ is 8x⁶. What is wrong with her reasoning?

Self Check

(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

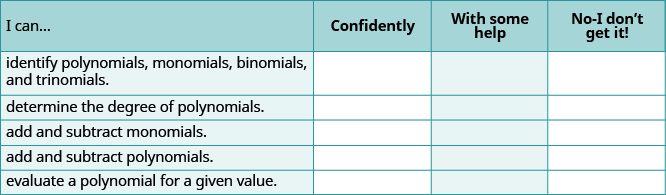
(b) If most of your checks were:

…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.

…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on.

Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?

…no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

Contributors and Attributions

• Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."