10.10: Introduction to Factoring Polynomials
- Page ID
- 5017
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Find the greatest common factor of two or more expressions
- Factor the greatest common factor from a polynomial
Before you get started, take this readiness quiz.
- Factor 56 into primes. If you missed this problem, review Example 2.9.1.
- Multiply: −3(6a + 11). If you missed this problem, review Example 7.4.9.
- Multiply: 4x2(x2 + 3x − 1). If you missed this problem, review Example 10.4.5.
Find the Greatest Common Factor of Two or More Expressions
Earlier we multiplied factors together to get a product. Now, we will be reversing this process; we will start with a product and then break it down into its factors. Splitting a product into factors is called factoring.
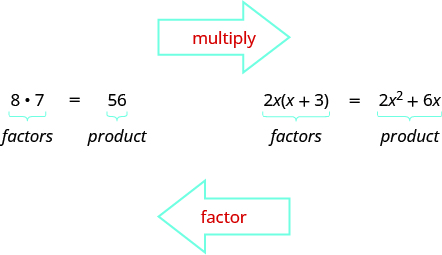
In The Language of Algebra we factored numbers to find the least common multiple (LCM) of two or more numbers. Now we will factor expressions and find the greatest common factor of two or more expressions. The method we use is similar to what we used to find the LCM.
The greatest common factor (GCF) of two or more expressions is the largest expression that is a factor of all the expressions.
First we will find the greatest common factor of two numbers
Find the greatest common factor of 24 and 36.
Solution
| Step 1: Factor each coefficient into primes. Write all variables with exponents in expanded form. | Factor 24 and 36. | 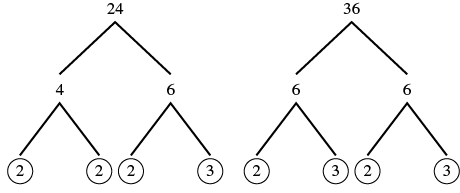 |
| Step 2: List all factors—matching common factors in a column. |  |
|
| In each column, circle the common factors. | Circle the 2, 2, and 3 that are shared by both numbers. |  |
| Step 3: Bring down the common factors that all expressions share. | Bring down the 2, 2, 3 and then multiply. | |
| Step 4: Multiply the factors. | The GCF of 24 and 36 is 12. |
Notice that since the GCF is a factor of both numbers, 24 and 36 can be written as multiples of 12.
\[\begin{split} 24 &= 12 \cdot 2 \\ 36 &= 12 \cdot 3 \end{split}\]
Find the greatest common factor: 54, 36.
- Answer
-
18
Find the greatest common factor: 48, 80.
- Answer
-
16
In the previous example, we found the greatest common factor of constants. The greatest common factor of an algebraic expression can contain variables raised to powers along with coefficients. We summarize the steps we use to find the greatest common factor.
Step 1. Factor each coefficient into primes. Write all variables with exponents in expanded form.
Step 2. List all factors—matching common factors in a column. In each column, circle the common factors.
Step 3. Bring down the common factors that all expressions share.
Step 4. Multiply the factors.
Find the greatest common factor of 5x and 15.
Solution
|
Factor each number into primes. Circle the common factors in each column. Bring down the common factors. |
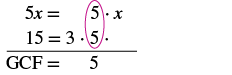 |
The GCF of 5x and 15 is 5.
Find the greatest common factor: 7y, 14.
- Answer
-
7
Find the greatest common factor: 22, 11m.
- Answer
-
11
In the examples so far, the greatest common factor was a constant. In the next two examples we will get variables in the greatest common factor.
Find the greatest common factor of 12x2 and 18x3.
Solution
|
Factor each coefficient into primes and write the variables with exponents in expanded form. Circle the common factors in each column. Bring down the common factors. Multiply the factors. |
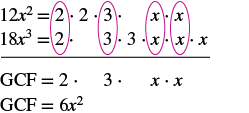 |
The GCF of 12x2 and 18x3 is 6x2.
Find the greatest common factor: 16x2, 24x3.
- Answer
-
\(8x^2\)
Find the greatest common factor: 27y3, 18y4.
- Answer
-
\(9y^3\)
Find the greatest common factor of 14x3, 8x2, 10x.
Solution
|
Factor each coefficient into primes and write the variables with exponents in expanded form. Circle the common factors in each column. Bring down the common factors. Multiply the factors. |
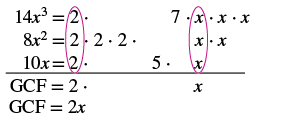 |
The GCF of 14x3 and 8x2, and 10x is 2x.
Find the greatest common factor: 21x3, 9x2, 15x.
- Answer
-
3x
Find the greatest common factor: 25m4, 35m3, 20m2.
- Answer
-
\(5m^2\)
Factor the Greatest Common Factor from a Polynomial
Just like in arithmetic, where it is sometimes useful to represent a number in factored form (for example, 12 as 2 • 6 or 3 • 4), in algebra it can be useful to represent a polynomial in factored form. One way to do this is by finding the greatest common factor of all the terms. Remember that you can multiply a polynomial by a monomial as follows:
\[\begin{split} 2(x &+ 7) \quad factors \\ 2 \cdot x &+ 2 \cdot 7 \\ 2x &+ 14 \quad product \end{split}\]
Here, we will start with a product, like 2x + 14, and end with its factors, 2(x + 7). To do this we apply the Distributive Property “in reverse”.
If a, b, c are real numbers, then a(b + c) = ab + ac and ab + ac = a(b + c).
The form on the left is used to multiply. The form on the right is used to factor.
So how do we use the Distributive Property to factor a polynomial? We find the GCF of all the terms and write the polynomial as a product!
Factor: 2x + 14.
Solution
| Step 1: Find the GCF of all the terms of the polynomial. | Find the GCF of 2x and 14. | 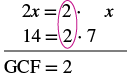 |
| Step 2: Rewrite each term as a product using the GCF. | Rewrite 2x and 14 as products of their GCF, 2.$$\begin{split} 2x &= 2 \cdot x \\ 14 &= 2 \cdot 7 \end{split}$$ | $$\begin{split} 2x &+ 14 \\ \textcolor{red}{2} \cdot x &+ \textcolor{red}{2} \cdot 7 \end{split}$$ |
| Step 3: Use the Distributive Property 'in reverse' to factor the expression. | 2(x + 7) | |
| Step 4: Check by multiplying the factors. | Check. | $$\begin{split} 2(x &+ 7) \\ 2 \cdot x &+ 2 \cdot 7 \\ 2x &+ 14\; \checkmark \end{split}$$ |
Factor: 4x + 12.
- Answer
-
4(x + 3)
Factor: 6a + 24.
- Answer
-
6(a + 4)
Notice that in Example 10.84, we used the word factor as both a noun and a verb:
| Noun | 7 is a factor of 14 |
| Verb | Factor 2 from 2x + 14 |
Step 1. Find the GCF of all the terms of the polynomial.
Step 2. Rewrite each term as a product using the GCF.
Step 3. Use the Distributive Property ‘in reverse’ to factor the expression.
Step 4. Check by multiplying the factors.
Factor: 3a + 3.
Solution
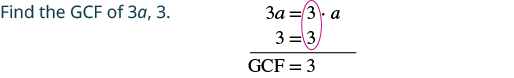 |
|
| Rewrite each term as a product using the GCF. | $$\textcolor{red}{3} \cdot a + \textcolor{red}{3} \cdot 1$$ |
| Use the Distributive Property 'in reverse' to factor the GCF. | $$3(a+1)$$ |
| Check by multiplying the factors to get the original polynomial. | $$\begin{split} 3(a &+ 1) \\ 3 \cdot a &= 3 \cdot 1 \\ 3a &+ 3\; \checkmark \end{split}$$ |
Factor: 9a + 9.
- Answer
-
9(a + 1)
Factor: 11x + 11.
- Answer
-
11(x + 1)
The expressions in the next example have several factors in common. Remember to write the GCF as the product of all the common factors.
Factor: 12x − 60.
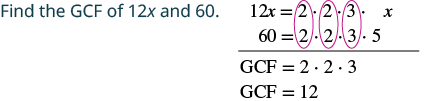 |
|
| Rewrite each term as a product using the GCF. | $$\textcolor{red}{12} \cdot x - \textcolor{red}{12} \cdot 5$$ |
| Factor the GCF. | $$12(x-5)$$ |
| Check by multiplying the factors. | $$\begin{split} 12(x &- 5) \\ 12 \cdot x &- 12 \cdot 5 \\ 12x &- 60\; \checkmark \end{split}$$ |
Factor: 11x − 44.
- Answer
-
11(x - 4)
Factor: 13y − 52.
- Answer
-
13(y - 4)
Now we’ll factor the greatest common factor from a trinomial. We start by finding the GCF of all three terms.
Factor: 3y2 + 6y + 9.
Solution
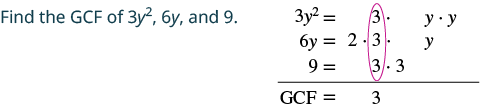 |
|
| Rewrite each term as a product using the GCF. | $$\textcolor{red}{3} \cdot y^{2} + \textcolor{red}{3} \cdot 2y + \textcolor{red}{3} \cdot 3$$ |
| Factor the GCF. | $$3(y^{2} + 2y + 3)$$ |
| Check by multiplying. | $$\begin{split} 3(y^{2} &+ 2y + 3) \\ 3 \cdot y^{2} &+ 3 \cdot 2y + 3 \cdot 3 \\ 3y^{2} &+ 6y + 9\; \checkmark \end{split}$$ |
Factor: 4y2 + 8y + 12.
- Answer
-
\(4\left(y^{2}+2 y+3\right) \)
Factor: 6x2 + 42x − 12.
- Answer
-
\( 6\left(x^{2}+7 x-2\right) \)
In the next example, we factor a variable from a binomial.
Factor: 6x2 + 5x.
Solution
| Find the GCF of 6x2 and 5x and the math that goes with it. | 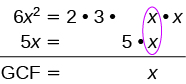 |
| Rewrite each term as a product. | $$\textcolor{red}{x} \cdot 6x + \textcolor{red}{x} \cdot 5$$ |
| Factor the GCF. | $$x(6x + 5)$$ |
| Check by multiplying. | $$\begin{split} x(6x &+ 5) \\ x \cdot 6x &+ x \cdot 5 \\ 6x^{2} &+ 5x\; \checkmark \end{split}$$ |
Factor: 9x2 + 7x.
- Answer
-
\( x(9x+7) \)
Factor: 5a2 − 12a.
- Answer
-
a(5a - 12)
When there are several common factors, as we’ll see in the next two examples, good organization and neat work helps!
Factor: 4x3 − 20x2.
Solution
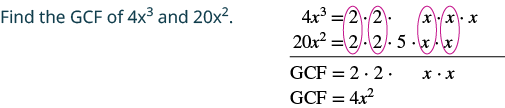 |
|
| Rewrite each term. | $$\textcolor{red}{4x^{2}} \cdot x - \textcolor{red}{4x^{2}} \cdot 5$$ |
| Factor the GCF. | $$4x^{2} (x-5)$$ |
| Check. | $$\begin{split} 4x^{2} (x &- 5) \\ 4x^{2} \cdot x &- 4x^{2} \cdot 5 \\ 4x^{3} &- 20x^{2}\; \checkmark \end{split}$$ |
Factor: 2x3 + 12x2.
- Answer
-
\( 2 x^{2}(x+6) \)
Factor: 6y3 − 15y2.
- Answer
-
\( 3 y^{2}(2 y-5) \)
Factor: 21y2 + 35y.
Solution
| Find the GCF of 21y2 and 35y. | 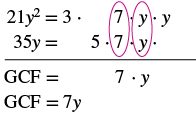 |
| Rewrite each term. | $$\textcolor{red}{7y} \cdot 3y + \textcolor{red}{7y} \cdot 5$$ |
| Factor the GCF. | $$7y(3y + 5)$$ |
Factor: 18y2 + 63y.
- Answer
-
9y(2y + 7)
Factor: 32k2 + 56k.
- Answer
-
8k(4k + 7)
Factor: 14x3 + 8x2 − 10x.
Solution
Previously, we found the GCF of 14x3, 8x2, and 10x to be 2x.
| Rewrite each term using the GCF, 2x. | $$\textcolor{red}{2x} \cdot 7x^{2} + \textcolor{red}{2x} \cdot 4x - \textcolor{red}{2x} \cdot 5$$ |
| Factor the GCF. | $$2x(7x^{2} + 4x - 5)$$ |
| Check. | $$\begin{split} 2x(7x^{2} &+ 4x - 5) \\ 2x \cdot 7x^{2} &+ 2x \cdot 4x - 2x \cdot 5 \\ 14x^{3} &+ 8x^{2} - 10x\; \checkmark \end{split}$$ |
Factor: 18y3 − 6y2 − 24y.
- Answer
-
\(6 y\left(3 y^{2}-y-4\right)\)
Factor: 16x3 + 8x2 − 12x.
- Answer
-
\(4 x\left(4 x^{2}+2 x-3\right)\)
When the leading coefficient, the coefficient of the first term, is negative, we factor the negative out as part of the GCF.
Factor: −9y − 27.
Solution
| When the leading coefficient is negative, the GCF will be negative. Ignoring the signs of the terms, we first find the GCF of 9y and 27 is 9. | 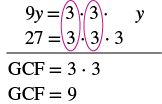 |
| Since the expression −9y − 27 has a negative leading coefficient, we use −9 as the GCF. | |
| Rewrite each term using the GCF. | $$\textcolor{red}{-9} \cdot y + (\textcolor{red}{-9}) \cdot 3$$ |
| Factor the GCF. | $$-9(y+3)$$ |
| Check. | $$\begin{split} -9(y &+ 3) \\ -9 \cdot y &+ (-9) \cdot 3 \\ -9y &- 27\; \checkmark \end{split}$$ |
Factor: −5y − 35.
- Answer
-
-5(y + 7)
Factor: −16z − 56.
- Answer
-
-8(2z + 7)
Pay close attention to the signs of the terms in the next example.
Factor: −4a2 + 16a.
Solution
| The leading coefficient is negative, so the GCF will be negative. | 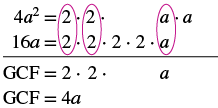 |
| Since the leading coefficient is negative, the GCF is negative, −4a. | |
| Rewrite each term. | $$\textcolor{red}{-4a} \cdot a - (\textcolor{red}{-4a}) \cdot 4$$ |
| Factor the GCF. | $$-4a(a-4)$$ |
| Check on your own by multiplying. |
Factor: −7a2 + 21a.
- Answer
-
-7a(a - 3)
Factor: −6x2 + x.
- Answer
-
-x(6x - 1)
Factor GCF
Factor a Binomial
Identify GCF
Practice Makes Perfect
Find the Greatest Common Factor of Two or More Expressions
In the following exercises, find the greatest common factor.
- 40, 56
- 45, 75
- 72, 162
- 150, 275
- 3x, 12
- 4y, 28
- 10a, 50
- 5b, 30
- 16y, 24y2
- 9x, 15x2
- 18m3, 36m2
- 12p4, 48p3
- 10x, 25x2, 15x3
- 18a, 6a2, 22a3
- 24u, 6u2, 30u3
- 40y, 10y2, 90y3
- 15a4, 9a5, 21a6
- 35x3, 10x4, 5x5
- 27y2, 45y3, 9y4
- 14b2, 35b3, 63b4
Factor the Greatest Common Factor from a Polynomial
In the following exercises, factor the greatest common factor from each polynomial.
- 2x + 8
- 5y + 15
- 3a − 24
- 4b − 20
- 9y − 9
- 7x − 7
- 5m2 + 20m + 35
- 3n2 + 21n + 12
- 8p2 + 32p + 48
- 6q2 + 30q + 42
- 8q2 + 15q
- 9c2 + 22c
- 13k2 + 5k
- 17x2 + 7x
- 5c2 + 9c
- 4q2 + 7q
- 5p2 + 25p
- 3r2 + 27r
- 24q2 − 12q
- 30u2 − 10u
- yz + 4z
- ab + 8b
- 60x − 6x3
- 55y − 11y4
- 48r4 − 12r3
- 45c3 − 15c2
- 4a3 − 4ab2
- 6c3 − 6cd2
- 30u3 + 80u2
- 48x3 + 72x2
- 120y6 + 48y4
- 144a6 + 90a3
- 4q2 + 24q + 28
- 10y2 + 50y + 40
- 15z2 − 30z − 90
- 12u2 − 36u − 108
- 3a4 − 24a3 + 18a2
- 5p4 − 20p3 − 15p2
- 11x6 + 44x5 − 121x4
- 8c5 + 40c4 − 56c3
- −3n − 24
- −7p − 84
- −15a2 − 40a
- −18b2 − 66b
- −10y3 + 60y2
- −8a3 + 32a2
- −4u5 + 56u3
- −9b5 + 63b3
Everyday Math
- Revenue A manufacturer of microwave ovens has found that the revenue received from selling microwaves a cost of p dollars each is given by the polynomial −5p2 + 150p. Factor the greatest common factor from this polynomial.
- Height of a baseball The height of a baseball hit with velocity 80 feet/second at 4 feet above ground level is −16t2 + 80t + 4, with t = the number of seconds since it was hit. Factor the greatest common factor from this polynomial.
Writing Exercises
- The greatest common factor of 36 and 60 is 12. Explain what this means.
- What is the GCF of y4, y5, and y10? Write a general rule that tells how to find the GCF of ya, yb, and yc.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
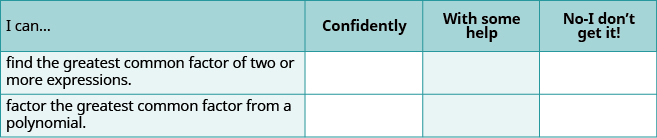
(b) Overall, after looking at the checklist, do you think you are well-prepared for the next Chapter? Why or why not?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


