4.1: Factions of Whole Numbers

Last updated
Save as PDF

Page ID: 48850

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Learning Objectives

understand the concept of fractions of whole numbers
be able to recognize the parts of a fraction

More Numbers on the Number Line

In Chapters [link], [link], and [link], we studied the whole numbers and methods of combining them. We noted that we could visually display the whole numbers by drawing a number line and placing closed circles at whole number locations.

$A number line with dots on the whole numbers.$

By observing this number line, we can see that the whole numbers do not account for every point on the line. What numbers, if any, can be associated with these points? In this section we will see that many of the points on the number line, including the points already associated with whole numbers, can be associated with numbers called fractions.

Fractions of Whole Numbers

The Nature of the Positive Fractions
We can extend our collection of numbers, which now contains only the whole numbers, by including fractions of whole numbers. We can determine the nature of these fractions using the number line.

If we place a pencil at some whole number and proceed to travel to the right to the next whole number, we see that our journey can be broken into different types of equal parts as shown in the following examples.

1 part.
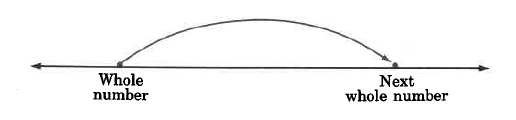
$A number line. Two marks: one on the left, labeled, whole number, and one on the right, labeled next whole number. An arrow is drawn from the whole number to the next whole number.$
2 equal parts.
$A number line. Two marks: one on the left, labeled, whole number, and one on the right, labeled next whole number. In between the two marks is the midway point. An arrow is drawn from the whole number to the midway point, and then from the midway point to the next whole number.$
3 equal parts.
$A number line. Two marks: one on the left, labeled, whole number, and one on the right, labeled next whole number. There are three arrows, connecting the two whole numbers and two evenly-spaced hash marks in between the whole numbers.$
4 equal parts.
$A number line. Two marks: one on the left, labeled, whole number, and one on the right, labeled next whole number. There are four arrows, connecting the two whole numbers and three evenly-spaced hash marks in between the whole numbers.$

The Latin Word Fractio

Notice that the number of parts, 2, 3, and 4, that we are breaking the original quantity into is always a nonzero whole number. The idea of breaking up a whole quantity gives us the word fraction. The word fraction comes from the Latin word "fractio" which means a breaking, or fracture.

Suppose we break up the interval from some whole number to the next whole number into five equal parts.

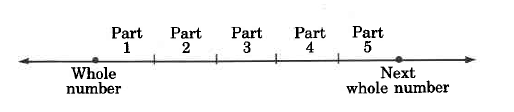
$A number line. Two marks: one on the left, labeled whole number, and one on the right, labeled next whole number. There are four hash marks in between the two whole numbers, creating five spaces of equal width, labeled Part 1 through Part 5.$

After starting to move from one whole number to the next, we decide to stop after covering only two parts. We have covered 2 parts of 5 equal parts. This situation is described by writing $\dfrac{2}{5}$.

$A number line. Two marks: one on the left, labeled whole number, and one on the right, labeled next whole number. There are four evenly-spaced hash marks in between the two marks. There is an arrow from the whole number to the first hash mark, and an arrow from the first hash mark to the second hash mark.$

Definition: Positive Fraction

A number such as $\dfrac{2}{5}$ is called a positive fraction, or more simply, a fraction.

The Parts of a Fraction

A fraction has three parts.

The fraction bar -.

Fraction Bar
The fraction bar serves as a grouping symbol. It separates a quantity into individual groups. These groups have names, as noted in 2 and 3 below.
The nonzero number below the fraction bar.

Denominator
This number is called the denominator of the fraction, and it indicates the number of parts the whole quantity has been divided into. Notice that the denominator must be a nonzero whole number since the least number of parts any quantity can have is one.
The number above the fraction bar.

Numerator
This number is called the numerator of the fraction, and it indicates how many of the specified parts are being considered. Notice that the numerator can be any whole number (including zero) since any number of the specified parts can be considered.
$\dfrac{\text{whole number}}{\text{nonzero whole number}} \leftrightarrow \dfrac{\text{numerator}}{\text{denominator}}$

Sample Set A

The diagrams in the following problems are illustrations of fractions.

Diagrams: $A whole circle.$ $A whole circle divided into 3 equal parts.$ $A whole circle divided into 3 equal parts. One of the parts is shaded.$
1a: A whole circle 1b: The whole circle divided into 3 equal parts 1c: 1 of the 3 equal parts

Figure 1.

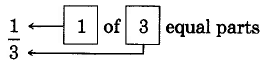
$The fraction one-third. This would be read, 1 of 3 equal parts.$

The fraction $\dfrac{1}{3}$ is read as "one third".

Sample Set A

Diagrams: $A rectangle.$ $A rectangle divided into five equal parts by vertical bars.$ $A rectangle divided into five equal parts by vertical bars. The three leftmost bars are shaded.$
2a: A whole rectangle 2b: The whole rectangle divided into 5 equal parts 2c: 3 of the 5 equal parts

Figure 2.

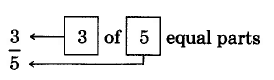
$The fraction three-fifths. This would be read, 3 of 5 equal parts.$

The fraction $\dfrac{3}{5}$ "is read as "three fifths."

Sample Set A

$A number line with two marks, 0 and 1.$
3a: The number line between 0 and 1

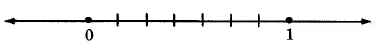
$A number line with two marks, 0, and 1, and six hash marks in between.$
3b: The number line between 0 and 1 divided into 7 equal parts

$A number line with two marks, 0, and 1, and six hash marks in between. There is an arrow drawn from the zero to the first hash mark, and then from that hash mark to the next, until the sixth hash mark, where the arrows stop.$
3c: 6 of the 7 equal parts

Figure 3.

$The fraction six-sevenths. This would be read, 6 of the 7 equal parts.$

The fraction $\dfrac{6}{7}$ is read as "six sevenths."

Sample Set A

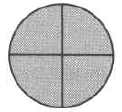
$A whole circle.$ $A whole circle divided into four equal parts.$ $A whole circle divided into four equal parts. All four parts are shaded.$
4a: A whole circle 4b: The whole circle divided into 4 equal parts 4c: 4 of the 4 equal parts

Figure 4.

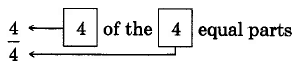
$The fraction four-fourths. This would be read, 4 of the 4 equal parts.$

When the numerator and denominator are equal, the fraction represents the entire quantity, and its value is 1.

$\dfrac{\text{nonzero whole number}}{\text{same nonzero whole number}} = 1$

Practice Set A

Specify the numerator and denominator of the following fractions.

$\dfrac{4}{7}$

Answer: 4, 7

Practice Set A

$\dfrac{5}{8}$

Answer: 5, 8

Practice Set A

$\dfrac{10}{15}$

Answer: 10, 15

Practice Set A

$\dfrac{1}{9}$

Answer: 1, 9

Practice Set A

$\dfrac{0}{2}$

Answer: 0, 2

Reading and Writing Fractions

In order to properly translate fractions from word form to number form, or from number form to word form, it is necessary to understand the use of the hyphen.

Use of the Hyphen
One of the main uses of the hyphen is to tell the reader that two words not ordinarily joined are to be taken in combination as a unit. Hyphens are always used for numbers between and including 21 and 99 (except those ending in zero).

Sample Set B

Write each fraction using whole numbers.

Fifty three-hundredths. The hyphen joins the words three and hundredths and tells us to consider them as a single unit. Therefore, fifty three-hundredths translates as $\dfrac{50}{300}$

Sample Set B

Fifty-three hundredths. The hyphen joins the numbers fifty and three and tells us to consider them as a single unit. Therefore, fifty-three hundredths translates as $\dfrac{53}{100}$

Sample Set B

Four hundred seven-thousandths. The hyphen joins the words seven and thousandths and tells us to consider them as a single unit. Therefore, four hundred seven-thousandths translates as $\dfrac{400}{7,000}$

Sample Set B

Four hundred seven thousandths. The absence of hyphens indicates that the words seven and thousandths are to be considered individually. four hundred seven thousandths translates as $\dfrac{407}{1000}$

Write each fraction using words.

Sample Set B

$\dfrac{21}{85}$ translates as twenty-one eighty-fifths.

Sample Set B

$\dfrac{200}{3,000}$ translates as two hundred three-thousandths. A hyphen is needed between the words three and thousandths to tell the reader that these words are to be considered as a single unit.

Sample Set B

$\dfrac{203}{1,000}$ translates as two hundred three thousandths.

Practice Set B

Write the following fractions using whole numbers.

one tenth

Answer: $\dfrac{1}{10}$

Practice Set B

eleven fourteenths

Answer: $\dfrac{11}{14}$

Practice Set B

sixteen thirty-fifths

Answer: $\dfrac{16}{35}$

Practice Set B

eight hundred seven-thousandths

Answer: $\dfrac{800}{7,000}$

Write the following using words.

Practice Set B

$\dfrac{3}{8}$

Answer: three eighths

Practice Set B

$\dfrac{1}{10}$

Answer: one tenth

Practice Set B

$\dfrac{3}{250}$

Answer: three two hundred fiftieths

Practice Set B

$\dfrac{114}{3,190}$

Answer: one hundred fourteen three thousand one hundred ninetieths

Name the fraction that describes each shaded portion.

Practice Set B

$A whole circle divided into eight equal parts, with three parts shaded.$

Answer: $\dfrac{3}{8}$

Practice Set B

$A whole circle divided into sixteen equal parts, with one part shaded.$

Answer: $\dfrac{1}{16}$

In the following 2 problems, state the numerator and denominator, and write each fraction in words.

Practice Set B

The number $\dfrac{5}{9}$ is used in converting from Fahrenheit to Celsius.

Answer: 5, 9, five ninths

Practice Set B

A dime is $\dfrac{1}{10}$ of a dollar.

Answer: 1, 10, one tenth

Exercises

For the following 10 problems, specify the numerator and denominator in each fraction.

Exercise $\PageIndex{1}$

$\dfrac{3}{4}$

Answer: numerator, 3; denominator, 4

Exercise $\PageIndex{2}$

$\dfrac{9}{10}$

Exercise $\PageIndex{3}$

$\dfrac{1}{5}$

Answer: numerator, 1; denominator, 5

Exercise $\PageIndex{4}$

$\dfrac{5}{6}$

Exercise $\PageIndex{5}$

$\dfrac{7}{7}$

Answer: numerator, 7; denominator, 7

Exercise $\PageIndex{6}$

$\dfrac{4}{6}$

Exercise $\PageIndex{7}$

$\dfrac{0}{12}$

Answer: numerator, 0; denominator, 12

Exercise $\PageIndex{8}$

$\dfrac{25}{25}$

Exercise $\PageIndex{9}$

$\dfrac{18}{1}$

Answer: numerator, 18; denominator, 1

Exercise $\PageIndex{10}$

$\dfrac{0}{16}$

For the following 10 problems, write the fractions using whole numbers.

Exercise $\PageIndex{11}$

four fifths

Answer: $\dfrac{4}{5}$

Exercise $\PageIndex{12}$

two ninths

Exercise $\PageIndex{13}$

fifteen twentieths

Answer: $\dfrac{15}{20}$

Exercise $\PageIndex{14}$

forty-seven eighty-thirds

Exercise $\PageIndex{15}$

ninety-one one hundred sevenths

Answer: $\dfrac{91}{107}$

Exercise $\PageIndex{16}$

twenty-two four hundred elevenths

Exercise $\PageIndex{17}$

six hundred five eight hundred thirty-fourths

Answer: $\dfrac{605}{834}$

Exercise $\PageIndex{18}$

three thousand three forty-four ten-thousandths

Exercise $\PageIndex{19}$

ninety-two one-millionths

Answer: $\dfrac{92}{1,000,000}$

Exercise $\PageIndex{20}$

one three-billionths

For the following 10 problems, write the fractions using words.

Exercise $\PageIndex{21}$

$\dfrac{5}{9}$

Answer: five ninths

Exercise $\PageIndex{22}$

$\dfrac{6}{10}$

Exercise $\PageIndex{23}$

$\dfrac{8}{15}$

Answer: eight fifteenths

Exercise $\PageIndex{24}$

$\dfrac{10}{13}$

Exercise $\PageIndex{25}$

$\dfrac{75}{100}$

Answer: seventy-five one hundredths

Exercise $\PageIndex{26}$

$\dfrac{86}{135}$

Exercise $\PageIndex{27}$

$\dfrac{916}{1,014}$

Answer: nine hundred sixteen one thousand fourteenths

Exercise $\PageIndex{28}$

$\dfrac{501}{10,001}$

Exercise $\PageIndex{29}$

$\dfrac{18}{31,608}$

Answer: eighteen thirty-one thousand six hundred eighths

Exercise $\PageIndex{30}$

$\dfrac{1}{500,000}$

For the following 4 problems, name the fraction corresponding to the shaded portion.

Exercise $\PageIndex{31}$

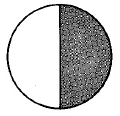
$A whole circle divided into two equal parts, with one part shaded.$

Answer: $\dfrac{1}{2}$

Exercise $\PageIndex{32}$

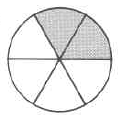
$A whole circle divided into six equal parts, with two parts shaded.$

Exercise $\PageIndex{33}$

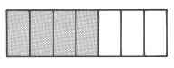
$A rectangle divided into seven equal parts, with four parts shaded.$

Answer: $\dfrac{4}{7}$

Exercise $\PageIndex{34}$

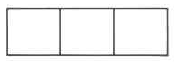
$A rectangle divided into three equal parts, with zero parts shaded.$

For the following 4 problems, shade the portion corresponding to the given fraction on the given figure.

Exercise $\PageIndex{35}$

$\dfrac{3}{5}$

$A rectangle divided into five equal parts.$

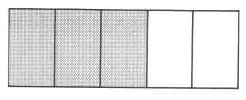
Answer: $A rectangle divided into five equal parts, with three parts shaded.$

Exercise $\PageIndex{36}$

$\dfrac{1}{8}$

$A circle divided into eight equal parts.$

Exercise $\PageIndex{37}$

$\dfrac{6}{6}$

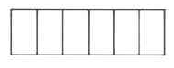
$A rectangle divided into six equal parts.$

Answer: $A rectangle divided into six equal parts, with all six parts shaded.$

Exercise $\PageIndex{38}$

$\dfrac{0}{3}$

$A circle divided into three equal parts.$

State the numerator and denominator and write in words each of the fractions appearing in the statements for the following 10 problems.

Exercise $\PageIndex{39}$

A contractor is selling houses on $\dfrac{1}{4}$ acre lots.

Answer: Numerator, 1; denominator, 4; one fourth

Exercise $\PageIndex{40}$

The fraction $\dfrac{22}{7}$ is sometimes used as an approximation to the number $\pi$. (The symbol is read “pi.")

Exercise $\PageIndex{41}$

The fraction $\dfrac{4}{3}$ is used in finding the volume of a sphere.

Answer: Numerator, 4; denominator, 3; four thirds

Exercise $\PageIndex{42}$

One inch is $\dfrac{1}{12}$ of a foot.

Exercise $\PageIndex{43}$

About $\dfrac{2}{7}$ of the students in a college statistics class received a “B” in the course.

Answer: Numerator, 2; denominator, 7; two sevenths

Exercise $\PageIndex{44}$

The probability of randomly selecting a club when drawing one card from a standard deck of 52 cards is $\dfrac{13}{52}$.

Exercise $\PageIndex{45}$

In a box that contains eight computer chips, five are known to be good and three are known to be defective. If three chips are selected at random, the probability that all three are defective is $\dfrac{1}{56}$.

Answer: Numerator, 1; denominator, 56; one fifty-sixth

Exercise $\PageIndex{46}$

In a room of 25 people, the probability that at least two people have the same birthdate (date and month, not year) is $\dfrac{569}{1000}$.

Exercise $\PageIndex{47}$

The mean (average) of the numbers 21, 25, 43, and 36 is $\dfrac{125}{4}$.

Answer: Numerator, 125; denominator, 4; one hundred twenty-five fourths

Exercise $\PageIndex{48}$

If a rock falls from a height of 20 meters on Jupiter, the rock will be $\dfrac{32}{25}$ meters high after $\dfrac{6}{5}$ seconds.

Exercises For Review

Exercise $\PageIndex{49}$

Use the numbers 3 and 11 to illustrate the commutative property of addition.

Answer: $3 + 11 = 11 + 3 = 14$

Exercise $\PageIndex{50}$

Find the quotient. $676 \div 26$

Exercise $\PageIndex{51}$

Write $7 \cdot 7 \cdot 7 \cdot 7 \cdot 7$ using exponents.

Answer: $7^5$

Exercise $\PageIndex{52}$

Find the value of $\dfrac{8 \cdot (6 + 20)}{8} + \dfrac{3 \cdot (6 + 16)}{22}$.

Exercise $\PageIndex{53}$

Find the least common multiple of 12, 16, and 18.

Answer: 144

Search

Text Color

Text Size

Margin Size

Font Type

Exercises For Review