4.2: Proper Fractions, Improper Fractions, and Mixed Numbers

Last updated
Save as PDF

Page ID: 48851

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Learning Objectives

be able to distinguish between proper fractions, improper fractions, and mixed numbers
be able to convert an improper fraction to a mixed number
be able to convert a mixed number to an improper fraction

Now that we know what positive fractions are, we consider three types of positive fractions: proper fractions, improper fractions, and mixed numbers.

Positive Proper Fractions

Definition: Positive Proper Fraction

Fractions in which the whole number in the numerator is strictly less than the whole number in the denominator are called positive proper fractions. On the number line, proper fractions are located in the interval from 0 to 1. Positive proper fractions are always less than one.

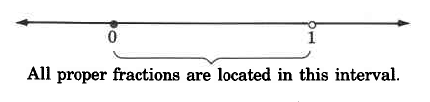
$A number line. 0 is marked with a black dot, and 1 is marked with a hollow dot. The distance between the two is labeled, all proper fractions are located in this interval.$

The closed circle at 0 indicates that 0 is included, while the open circle at 1 indicates that 1 is not included.

Some examples of positive proper fractions are

$\dfrac{1}{2}$, $\dfrac{3}{5}$, $\dfrac{20}{27}$, and $\dfrac{106}{255}$

Note that $1 < 2$, $3 < 5$, $20 < 27$, and $106 < 225$.

Positive Improper Fractions

Definition: Positive Improper Fractions

Fractions in which the whole number in the numerator is greater than or equal to the whole number in the denominator are called positive improper fractions. On the number line, improper fractions lie to the right of (and including) 1. Positive improper fractions are always greater than or equal to 1.

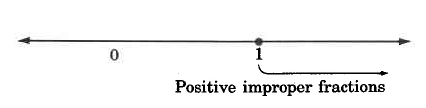
$A number line. 0 is labeled, and 1 is marked with a hollow dot. An arrow is drawn to the right, labeled Positive improper fractions.$

Some examples of positive improper fractions are

$\dfrac{3}{2}$, $\dfrac{8}{5}$, $\dfrac{4}{4}$, and $\dfrac{105}{16}$

Note that $3 \ge 2, 8 \ge 5, 4 \ge 4$, and $105 \ge 16$.

Positive Mixed Numbers

Definition: Positive Mixed Numbers

A number of the form $\text{nonzero whole number} + \text{proper fraction}$ is called a positive mixed number. For example, 2$\dfrac{3}{5}$ is a mixed number. On the number line, mixed numbers are located in the interval to the right of (and including) 1. Mixed numbers are always greater than or equal to 1.

$A number line. 0 is labeled, and 1 is marked with a hollow dot. An arrow is drawn to the right, labeled Positive mixed numbers.$

Relating Positive Improper Fractions and Positive Mixed Numbers

A relationship between improper fractions and mixed numbers is suggested by two facts. The first is that improper fractions and mixed numbers are located in the same interval on the number line. The second fact, that mixed numbers are the sum of a natural number and a fraction, can be seen by making the following observations.

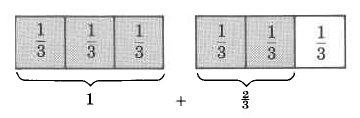
Divide a whole quantity into 3 equal parts.

$A rectangle divided into three equal parts with vertical bars. Each part contains the fraction, one-third.$

Now, consider the following examples by observing the respective shaded areas.

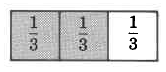
$A rectangle divided into three equal parts with vertical bars. Each part contains the fraction, one-third. The two leftmost parts are shaded.$

In the shaded region, there are 2 one thirds, or $\dfrac{2}{3}$.

$2 (\dfrac{1}{3}) = \dfrac{2}{3}$

$A rectangle divided into three equal parts with vertical bars. Each part contains the fraction, one-third. All three parts are shaded.$

There are 3 one thirds, or $\dfrac{3}{3}$, or 1.

$3(\dfrac{1}{3}) = \dfrac{3}{3}$ or 1

Thus,

$\dfrac{3}{3} = 1$

Improper fraction = whole number.

$A rectangle divided into three equal parts with vertical bars. Each part contains the fraction, one-third. All three parts are shaded.$ $A rectangle divided into three equal parts with vertical bars. Each part contains the fraction, one-third. One part is shaded.$

There are 4 one thirds, or $\dfrac{4}{3}$, or 1 and $\dfrac{1}{3}$.

$4(\dfrac{1}{3}) = \dfrac{4}{3}$ or 1 and $\dfrac{1}{3}$

The terms 1 and $\dfrac{1}{3}$ can be represented as $1 + \dfrac{1}{3}$ or $1 \dfrac{1}{3}$

Thus,

$\dfrac{4}{3} = 1 \dfrac{1}{3}.$

mproper fraction = mixed number.

There are 5 one thirds, or $\dfrac{5}{3}$, or 1 and $\dfrac{2}{3}$.

$5(\dfrac{1}{3}) = \dfrac{5}{3}$ or 1 and $\dfrac{2}{3}$

The terms 1 and $\dfrac{2}{3}$ can be represented as $1 + \dfrac{2}{3}$ or $1\dfrac{2}{3}$.

Thus,

$\dfrac{5}{3} = 1 \dfrac{2}{3}$.

Improper fraction = mixed number.

There are 6 one thirds, or $\dfrac{6}{3}$, or 2.

$6(\dfrac{1}{3}) = \dfrac{6}{3} = 2$

Thus,

$\dfrac{6}{3} = 2$

Improper fraction = whole number.

The following important fact is illustrated in the preceding examples.

Mixed Number = Natural Number + Proper Fraction
Mixed numbers are the sum of a natural number and a proper fraction. Mixed number = (natural number) + (proper fraction)

For example $1 \dfrac{1}{3}$ can be expressed as $1 + \dfrac{1}{3}$ The fraction $5 \dfrac{7}{8}$ can be expressed as $5 + \dfrac{7}{8}$.

It is important to note that a number such as $5 + \dfrac{7}{8}$ does not indicate multiplication. To indicate multiplication, we would need to use a multiplication symbol (such as $\cdot$)

Example $\PageIndex{1}$

$5 \dfrac{7}{8}$ means $5 + \dfrac{7}{8}$ and not $5 \cdot \dfrac{7}{8}$, which means 5 times $\dfrac{7}{8}$ or 5 multiplied by $\dfrac{7}{8}$.

Thus, mixed numbers may be represented by improper fractions, and improper fractions may be represented by mixed numbers.

Converting Improper Fractions to Mixed Numbers

To understand how we might convert an improper fraction to a mixed number, let's consider the fraction, $\dfrac{4}{3}$.

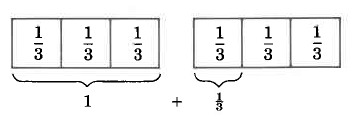
$\begin{array} {rcl} {\dfrac{4}{3}} & = & {\underbrace{\dfrac{1}{3} + \dfrac{1}{3} + \dfrac{1}{3}}_{1} + \dfrac{1}{3}} \\ {} & = & {1 + \dfrac{1}{3}} \\ {} & = & {1\dfrac{1}{3}} \end{array}$

We can illustrate a procedure for converting an improper fraction to a mixed number using this example. However, the conversion is more easily accomplished by dividing the numerator by the denominator and using the result to write the mixed number.

Converting an Improper Fraction to a Mixed Number
To convert an improper fraction to a mixed number, divide the numerator by the denominator.

The whole number part of the mixed number is the quotient.
The fractional part of the mixed number is the remainder written over the divisor (the denominator of the improper fraction).

Sample Set A

Convert each improper fraction to its corresponding mixed number.

$\dfrac{5}{3}$ Divide 5 by 3.

Solution

$Long division. 5 divided by 3 is one, with a remainder of 2. 1 is the whole number part, 2 is the numerator of the fractional part, and 3 is the denominator of the fractional part.$

The improper fraction $\dfrac{5}{3} = 1 \dfrac{2}{3}$.

$A number line with marks for 0, 1, and 2. In between 1 and 2 is a dot for five thirds, or one and two thirds.$

Sample Set A

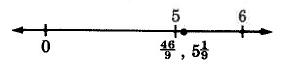
$\dfrac{46}{9}$ Divide 46 by 9.

Solution

$Long division. 46 divided by 9 is 5, with a remainder of 1. 5 is the whole number part, 1 is the numerator of the fractional part, and 9 is the denominator of the fractional part.$

The improper fraction $\dfrac{46}{9} = 5 \dfrac{1}{9}$.

$A number line with marks for 0, 5, and 6. In between 5 and 6 is a dot showing the location of forty-six ninths, or five and one ninth.$

Sample Set A

$\dfrac{83}{11}$ Divide 83 by 11.

Solution

$Long division. 83 divided by 11 is 7, with a remainder of 6. 7 is the whole number part, 6 is the numerator of the fractional part, and 11 is the denominator of the fractional part.$

The improper fraction $\dfrac{83}{11} = 7 \dfrac{6}{11}$.

$A number line with marks for 0, 7, and 8. In between 7 and 8 is a dot showing the location of eighty-three elevenths, or seven and six elevenths.$

Sample Set A

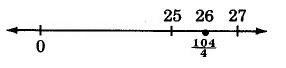
$\dfrac{104}{4}$ Divide 104 by 4.

Solution

$Long division. 104 divided by 4 is 26, with a remainder of 0. 26 is the whole number part, 0 is the numerator of the fractional part, and 4 is the denominator of the fractional part.$

\(\dfrac{104}{4} = 26 \dfrac{0}{4} = 26

The improper fraction $\dfrac{104}{4} = 26$.

$A number line with marks for 0, 25, 26, and 27. 26 is marked with a dot, showing the location of one hundred four fourths.$

Practice Set A

Convert each improper fraction to its corresponding mixed number.

$\dfrac{9}{2}$

Answer: $4\dfrac{1}{2}$

Practice Set A

$\dfrac{11}{3}$

Answer: $3\dfrac{2}{3}$

Practice Set A

$\dfrac{14}{11}$

Answer: $1\dfrac{3}{11}$

Practice Set A

$\dfrac{31}{13}$

Answer: $2\dfrac{5}{13}$

Practice Set A

$\dfrac{79}{4}$

Answer: $19\dfrac{3}{4}$

Practice Set A

$\dfrac{496}{8}$

Answer: 62

Converting Mixed Numbers to Improper Fractions

To understand how to convert a mixed number to an improper fraction, we'll recall

mixed number = (natural number) + (proper fraction)

and consider the following diagram.

$Two rectangles, each divided into three equal parts with vertical bars. Each part contains the fraction, one-third. Under the rectangle on the left is a bracket grouping all three parts together to make one. Under the rectangle on the right is a bracket under two of the three parts, making two thirds. The two bracketed segments are added together.$ $one and two thirds is equivalent to one plus two thirds. One can be expanded to three thirds, making the original number equivalent to the sum of five one-thirds, or five thirds.$

Recall that multiplication describes repeated addition.

Notice that $\dfrac{5}{3}$ can be obtained from $1 \dfrac{2}{3}$ using multiplication in the following way.

Multiply: $3 \cdot 1 = 3$

$one and two thirds, with an arrow drawn from the denominator to the one.$

Add: $3 + 2 = 5$. Place the 5 over the 3: $\dfrac{5}{3}$

The procedure for converting a mixed number to an improper fraction is illustrated in this example.

Converting a Mixed Number to an Improper Fraction
To convert a mixed number to an improper fraction,

Multiply the denominator of the fractional part of the mixed number by the whole number part.
To this product, add the numerator of the fractional part.
Place this result over the denominator of the fractional part.

Sample Set B

Convert each mixed number to an improper fraction.

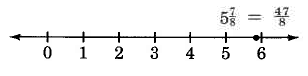
$5 \dfrac{7}{8}$

Solution

Multiply: $8 \cdot 5 = 40$
Add: $40 + 7 = 47$
Place 47 over 8: $\dfrac{47}{8}$

Thus, $5 \dfrac{7}{8} = \dfrac{47}{8}$.

$A number line showing the location of five and seven eigths, or 47 eights.$

Sample Set B

$16 \dfrac{2}{3}$

Solution

Multiply: $3 \cdot 16 = 48$.
Add: $48 + 2 = 50$
Place 50 over 3: $\dfrac{50}{3}$

Thus, $16 \dfrac{2}{3} = \dfrac{50}{3}$

Practice Set A

Convert each mixed number to its corresponding improper fraction.

$8 \dfrac{1}{4}$

Answer: $\dfrac{33}{4}$

Practice Set A

$5 \dfrac{3}{5}$

Answer: $\dfrac{28}{5}$

Practice Set A

$1 \dfrac{4}{15}$

Answer: $\dfrac{19}{15}$

Practice Set A

$12 \dfrac{2}{7}$

Answer: $\dfrac{86}{7}$

Exercises

For the following 15 problems, identify each expression as a proper fraction, an improper fraction, or a mixed number.

Exercise $\PageIndex{1}$

$\dfrac{3}{2}$

Answer: improper fraction

Exercise $\PageIndex{2}$

$\dfrac{4}{9}$

Exercise $\PageIndex{3}$

$\dfrac{5}{7}$

Answer: proper fraction

Exercise $\PageIndex{4}$

$\dfrac{1}{8}$

Exercise $\PageIndex{5}$

$6 \dfrac{1}{4}$

Answer: mixed number

Exercise $\PageIndex{6}$

$\dfrac{11}{8}$

Exercise $\PageIndex{7}$

$\dfrac{1,001}{12}$

Answer: improper fraction

Exercise $\PageIndex{8}$

$191 \dfrac{4}{5}$

Exercise $\PageIndex{9}$

$1 \dfrac{9}{13}$

Answer: mixed number

Exercise $\PageIndex{10}$

$31 \dfrac{6}{7}$

Exercise $\PageIndex{11}$

$3 \dfrac{1}{40}$

Answer: mixed number

Exercise $\PageIndex{12}$

$\dfrac{55}{12}$

Exercise $\PageIndex{13}$

$\dfrac{0}{9}$

Answer: proper fraction

Exercise $\PageIndex{14}$

$\dfrac{8}{9}$

Exercise $\PageIndex{15}$

$101 \dfrac{1}{11}$

Answer: mixed number

For the following 15 problems, convert each of the improper fractions to its corresponding mixed number.

Exercise $\PageIndex{16}$

$\dfrac{11}{6}$

Exercise $\PageIndex{17}$

$\dfrac{14}{3}$

Answer: $4 \dfrac{2}{3}$

Exercise $\PageIndex{18}$

$\dfrac{25}{4}$

Exercise $\PageIndex{19}$

$\dfrac{35}{4}$

Answer: $8 \dfrac{3}{4}$

Exercise $\PageIndex{20}$

$\dfrac{71}{8}$

Exercise $\PageIndex{21}$

$\dfrac{63}{7}$

Answer: 9

Exercise $\PageIndex{22}$

$\dfrac{121}{11}$

Exercise $\PageIndex{23}$

$\dfrac{165}{12}$

Answer: $13 \dfrac{9}{12}$ or $13 \dfrac{3}{4}$

Exercise $\PageIndex{24}$

$\dfrac{346}{15}$

Exercise $\PageIndex{25}$

$\dfrac{5,000}{9}$

Answer: $555 \dfrac{5}{9}$

Exercise $\PageIndex{26}$

$\dfrac{23}{5}$

Exercise $\PageIndex{27}$

$\dfrac{73}{2}$

Answer: $36 \dfrac{1}{2}$

Exercise $\PageIndex{28}$

$\dfrac{19}{2}$

Exercise $\PageIndex{29}$

$\dfrac{316}{41}$

Answer: $7 \dfrac{29}{41}$

Exercise $\PageIndex{30}$

$\dfrac{800}{3}$

For the following 15 problems, convert each of the mixed numbers to its corresponding improper fraction.

Exercise $\PageIndex{31}$

$4 \dfrac{1}{8}$

Answer: $\dfrac{33}{8}$

Exercise $\PageIndex{32}$

$1 \dfrac{5}{12}$

Exercise $\PageIndex{33}$

$6 \dfrac{7}{9}$

Answer: $\dfrac{61}{9}$

Exercise $\PageIndex{34}$

$15 \dfrac{1}{4}$

Exercise $\PageIndex{35}$

$10 \dfrac{5}{11}$

Answer: $\dfrac{115}{11}$

Exercise $\PageIndex{36}$

$15 \dfrac{3}{10}$

Exercise $\PageIndex{37}$

$8 \dfrac{2}{3}$

Answer: $\dfrac{26}{3}$

Exercise $\PageIndex{38}$

$4 \dfrac{3}{4}$

Exercise $\PageIndex{39}$

$21 \dfrac{2}{5}$

Answer: $\dfrac{107}{5}$

Exercise $\PageIndex{40}$

$17 \dfrac{9}{10}$

Exercise $\PageIndex{41}$

$9 \dfrac{20}{21}$

Answer: $\dfrac{209}{21}$

Exercise $\PageIndex{42}$

$5 \dfrac{1}{16}$

Exercise $\PageIndex{43}$

$90 \dfrac{1}{100}$

Answer: $\dfrac{9001}{100}$

Exercise $\PageIndex{44}$

$300 \dfrac{43}{1,000}$

Exercise $\PageIndex{45}$

$19 \dfrac{7}{8}$

Answer: $\dfrac{159}{8}$

Exercise $\PageIndex{46}$

Why does $0 \dfrac{4}{7}$ not qualify as a mixed number?

Hint:

See the definition of a mixed number.

Exercise $\PageIndex{47}$

Why does 5 qualify as a mixed number?

Hint:

See the definition of a mixed number.

Answer: ... because it may be wirtten as $5 \dfrac{0}{n}$, where $n$ is any positive whole number.

Calculator Problems
For the following 8 problems, use a calculator to convert each mixed number to its corresponding improper fraction.

Exercise $\PageIndex{48}$

$35 \dfrac{11}{12}$

Exercise $\PageIndex{49}$

$27 \dfrac{5}{61}$

Answer: $\dfrac{1,652}{61}$

Exercise $\PageIndex{50}$

$83 \dfrac{40}{41}$

Exercise $\PageIndex{51}$

$105 \dfrac{21}{23}$

Answer: $\dfrac{2,436}{23}$

Exercise $\PageIndex{52}$

$72 \dfrac{605}{606}$

Exercise $\PageIndex{53}$

$816 \dfrac{19}{25}$

Answer: $\dfrac{20,419}{25}$

Exercise $\PageIndex{54}$

$708 \dfrac{42}{51}$

Exercise $\PageIndex{55}$

$6,012 \dfrac{4,216}{8,117}$

Answer: $\dfrac{48,803,620}{8,117}$

Exercises For Review

Exercise $\PageIndex{56}$

Round 2,614,000 to the nearest thousand.

Exercise $\PageIndex{57}$

Find the product. $1,004 \cdot 1,005$

Answer: 1,009,020

Exercise $\PageIndex{58}$

Determine if 41,826 is divisible by 2 and 3.

Exercise $\PageIndex{59}$

Find the least common multiple of 28 and 36.

Answer: 252

Exercise $\PageIndex{60}$

Specify the numerator and denominator of the fraction $\dfrac{12}{19}$.