4.3: Equivalent Fractions, Reducing Fractions to Lowest Terms, and Raising Fractions to Higher Terms
( \newcommand{\kernel}{\mathrm{null}\,}\)
- be able to recognize equivalent fractions
- be able to reduce a fraction to lowest terms
- be able to raise a fraction to higher terms
Equivalent Fractions
Let's examine the following two diagrams.
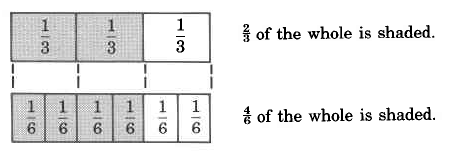
Notice that both
Fractions that have the same value are called equivalent fractions. Equivalent fractions may look different, but they are still the same point on the number line.
There is an interesting property that equivalent fractions satisfy.
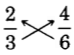
A Test for Equivalent Fractions Using the Cross Product
These pairs of products are called cross products.
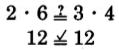
If the cross products are equal, the fractions are equivalent. If the cross products are not equal, the fractions are not equivalent.
Thus,
Determine if the following pairs of fractions are equivalent.
Solution
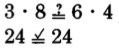
The cross products are equals.
The fractions
Solution
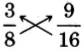
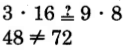
The cross products are equals.
The fractions
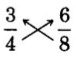
Practice Set A
Determine if the pairs of fractions are equivalent.
- Answer
-
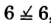
, yes
Practice Set A
- Answer
-
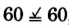
, yes
Practice Set A
- Answer
-
Practice Set A
- Answer
-
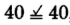
, yes
Practice Set A
- Answer
-
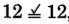
, yes
Reducing Fractions to Lowest Terms
It is often very useful to convert one fraction to an equivalent fraction that has reduced values in the numerator and denominator. We can suggest a method for doing so by considering the equivalent fractions
(Can you prove this?) So,
The fraction
A natural question is "Why did we choose to divide by 3?" Notice that
We can see that the factor 3 is common to both the numerator and denominator.
From these observations we can suggest the following method for converting one fraction to an equivalent fraction that has reduced values in the numerator and denominator. The method is called reducing a fraction.
A fraction can be reduced by dividing both the numerator and denominator by the same nonzero whole number.
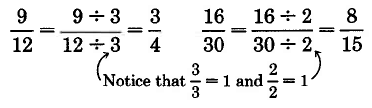
Consider the collection of equivalent fractions
Reduced to Lowest Terms
Notice that each of the first four fractions can be reduced to the last fraction,
Observe a very important property of a fraction that has been reduced to lowest terms. The only whole number that divides both the numerator and denominator without a remainder is the number 1. When 1 is the only whole number that divides two whole numbers, the two whole numbers are said to be relatively prime.
Relatively Prime
A fraction is reduced to lowest terms if its numerator and denominator are relatively prime.
Methods of Reducing Fractions to Lowest Terms
Method 1: Dividing Out Common Primes
- Write the numerator and denominator as a product of primes.
- Divide the numerator and denominator by each of the common prime factors. We often indicate this division by drawing a slanted line through each divided out factor. This process is also called cancelling common factors.
- The product of the remaining factors in the numerator and the product of remaining factors of the denominator are relatively prime, and this fraction is reduced to lowest terms.
Sample Set B
The fraction
Practice Set B
Reduce each fraction to lowest terms.
- Answer
-
Practice Set B
- Answer
-
Practice Set B
- Answer
-
Practice Set B
- Answer
-
Practice Set B
- Answer
-
Practice Set B
- Answer
-
Method 2: Dividing Out Common Factors
- Mentally divide the numerator and the denominator by a factor that is common to each. Write the quotient above the original number.
- Continue this process until the numerator and denominator are relatively prime.
Reduce each fraction to lowest terms.
Practice Set C
Reduce each fraction to lowest terms.
- Answer
-
Practice Set C
- Answer
-
Practice Set C
- Answer
-
Practice Set C
- Answer
-
Practice Set C
- Answer
-
Practice Set C
- Answer
-
Raising Fractions to Higher Terms
Equally as important as reducing fractions is raising fractions to higher terms. Raising a fraction to higher terms is the process of constructing an equivalent fraction that has higher values in the numerator and denominator than the original fraction.
The fractions
Notice that
From these observations we can suggest the following method for converting one fraction to an equivalent fraction that has higher values in the numerator and denominator. This method is called raising a fraction to higher terms.
Raising a Fraction to Higher Terms
A fraction can be raised to an equivalent fraction that has higher terms in the numerator and denominator by multiplying both the numerator and denominator by the same nonzero whole number.
The fraction
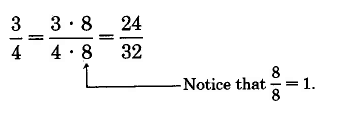
Most often, we will want to convert a given fraction to an equivalent fraction with a higher specified denominator. For example, we may wish to convert
This is possible to do because we know the process. We must multiply both the numerator and denominator of
We have some information. The denominator 8 was raised to 32 by multiplying it by some nonzero whole number. Division will give us the proper factor. Divide the original denominator into the new denominator.
Now, multiply the numerator 5 by 4.
Thus,
So,
Determine the missing numerator or denominator.
Practice Set D
Determine the missing numerator or denominator.
- Answer
-
32
Practice Set D
- Answer
-
12
Practice Set D
- Answer
-
4
Practice Set D
- Answer
-
150
Practice Set D
- Answer
-
88
Exercises
For the following problems, determine if the pairs of fractions are equivalent.
Exercise
- Answer
-
equivalent
Exercise
Exercise
- Answer
-
equivalent
Exercise
Exercise
- Answer
-
not equivalent
Exercise
Exercise
- Answer
-
not equivalent
Exercise
Exercise
- Answer
-
not equivalent
Exercise
Exercise
- Answer
-
equivalent
Exercise
Exercise
- Answer
-
not equivalent
Exercise
Exercise
- Answer
-
not equivalent
For the following problems, determine the missing numerator or denominator.
Exercise
Exercise
- Answer
-
6
Exercise
Exercise
- Answer
-
12
Exercise
Exercise
- Answer
-
20
Exercise
Exercise
- Answer
-
75
Exercise
Exercise
- Answer
-
48
Exercise
Exercise
- Answer
-
80
Exercise
Exercise
- Answer
-
18
Exercise
Exercise
- Answer
-
154
Exercise
Exercise
- Answer
-
1,472
Exercise
Exercise
- Answer
-
1,850
For the following problems, reduce, if possible, each of the fractions to lowest terms.
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
3
Exercise
Exercise
- Answer
-
2
Exercise
Exercise
- Answer
-
already reduced
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
Exercise
- Answer
-
Exercise
A ream of paper contains 500 sheets. What fraction of a ream of paper is 200 sheets? Be sure to reduce.
Exercise
There are 24 hours in a day. What fraction of a day is 14 hours?
- Answer
-
Exercise
A full box contains 80 calculators. How many calculators are in
Exercise
There are 48 plants per flat. How many plants are there in
- Answer
-
16
Exercise
A person making $18,000 per year must pay $3,960 in income tax. What fraction of this person's yearly salary goes to the IRS?
For the following problems, find the mistake.
Exercise
- Answer
-
Should be
Exercise
Exercise
- Answer
-
Cancel factors only, not addends;
Exercise
Exercise
- Answer
-
1
Exercises for Review
Exercise
Round 816 to the nearest thousand.
Exercise
Perform the division:
- Answer
-
0
Exercise
Find all the factors of 24.
Exercise
Find the greatest common factor of 12 and 18.
- Answer
-
6
Exercise
Convert


