4.4: Multiplication of Fractions

Last updated
Save as PDF

Page ID: 48853

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

understand the concept of multiplication of fractions
be able to multiply one fraction by another
be able to multiply mixed numbers
be able to find powers and roots of various fractions

Fractions of Fractions

We know that a fraction represents a part of a whole quantity. For example, two fifths of one unit can be represented by

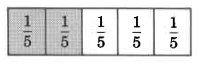
$A rectangle equally divided into five parts. Each part is labeled one-fifth. Two of the parts are shaded.$

$\dfrac{2}{5}$ of the whole is shaded.

A natural question is, what is a fractional part of a fractional quantity, or, what is a fraction of a fraction? For example, what $\dfrac{2}{3}$ of $\dfrac{1}{2}$?

We can suggest an answer to this question by using a picture to examine $\dfrac{2}{3}$ of $\dfrac{1}{2}$.

First, let's represent $\dfrac{1}{2}$.

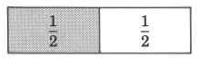
$A rectangle equally divided into two parts. Both parts are labeled one-half. One of the parts is shaded.$

$\dfrac{1}{2}$ of the whole is shaded.

Then divide each of the$\dfrac{1}{2}$ parts into 3 equal parts.

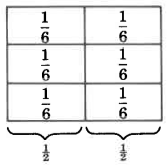
$A rectangle divided into six equal parts in a gridlike fashion, with three rows and two columns. Each part is labeled one-sixth. Below the rectangles are brackets showing that each column of sixths is equal to one-half.$

Each part is $\dfrac{1}{6}$ of the whole.

Now we'll take $\dfrac{2}{3}$ of the $\dfrac{1}{2}$ unit.

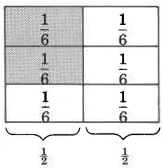
$\dfrac{2}{3}$ of $\dfrac{1}{2}$ is $\dfrac{2}{6}$, which reduces to $\dfrac{1}{3}$.

Multiplication of Fractions

Now we ask, what arithmetic operation $(+, - , \times , \div)$ will produce $\dfrac{2}{6}$ from $\dfrac{2}{3}$ of $\dfrac{1}{2}$?

Notice that, if in the fractions $\dfrac{2}{3}$ and $\dfrac{1}{2}$, we multiply the numerators together and the denominators together, we get precisely $\dfrac{2}{6}$.

$\dfrac{2 \cdot 1}{3 \cdot 2} = \dfrac{2}{6}$

This reduces to $\dfrac{1}{3}$ as before.

Using this observation, we can suggest the following:

The word "of" translates to the arithmetic operation "times."
To multiply two or more fractions, multiply the numerators together and then multiply the denominators together. Reduce if necessary.

$\dfrac{\text{numerator 1}}{\text{denominator 1}} \cdot \dfrac{\text{numerator 2}}{\text{denominator 2}} = \dfrac{\text{numerator 1}}{\text{denominator 1}} \cdot \dfrac{\text{numerator 2}}{\text{denominator 2}}$

Sample Set A

Perform the following multiplications.

$\dfrac{3}{4} \cdot \dfrac{1}{6} = \dfrac{3 \cdot 1}{4 \cdot 6} = \dfrac{3}{24}$ Now, reduce,

$= \dfrac{\begin{array} {c} {^1} \\ {\cancel{3}} \end{array}}{\begin{array} {c} {\cancel{24}} \\ {^{8}} \end{array}} = \dfrac{1}{8}$

Thus

$\dfrac{3}{4} \cdot \dfrac{1}{6} = \dfrac{1}{8}$

This means that $\dfrac{3}{4}$ of $\dfrac{1}{6}$ is $\dfrac{1}{8}$, that is, $\dfrac{3}{4}$ of $\dfrac{1}{6}$ of a unit is $\dfrac{1}{8}$ of the original unit.

Sample Set A

$\dfrac{3}{8} \cdot 4$. Write 4 as a fraction by writing $\dfrac{4}{1}$

$\dfrac{3}{8} \cdot \dfrac{4}{1} = \dfrac{3 \cdot 4}{8 \cdot 1} = \dfrac{12}{8} = \dfrac{\begin{array} {c} {^3} \\ {\cancel{12}} \end{array}}{\begin{array} {c} {\cancel{8}} \\ {^2} \end{array}} = \dfrac{3}{2}$

$\dfrac{3}{8} \cdot 4 = \dfrac{3}{2}$

This means that $\dfrac{3}{8}$ of 4 whole units is $\dfrac{3}{2}$ of one whole unit.

Sample Set A

$\dfrac{2}{5} \cdot \dfrac{5}{8} \cdot \dfrac{1}{4} = \dfrac{2 \cdot 5 \cdot 1}{5 \cdot 8 \cdot 4} = \dfrac{\begin{array} {c} {^1} \\ {\cancel{10}} \end{array}}{\begin{array} {c} {\cancel{160}} \\ {^{16}} \end{array}} = \dfrac{1}{16}$

This means that $\dfrac{2}{5}$ of $\dfrac{5}{8}$ of $\dfrac{1}{4}$ of a whole unit is $\dfrac{1}{16}$ of the original unit.

Practice Set A

Perform the following multiplications.

$\dfrac{2}{5} \cdot \dfrac{1}{6}$

Answer: $\dfrac{1}{15}$

Practice Set A

$\dfrac{1}{4} \cdot \dfrac{8}{9}$

Answer: $\dfrac{2}{9}$

Practice Set A

$\dfrac{4}{9} \cdot \dfrac{15}{16}$

Answer: $\dfrac{5}{12}$

Practice Set A

$(\dfrac{2}{3}) (\dfrac{2}{3})$

Answer: $\dfrac{4}{9}$

Practice Set A

$(\dfrac{7}{4}) (\dfrac{8}{5})$

Answer: $\dfrac{14}{5}$

Practice Set A

$\dfrac{5}{6} \cdot \dfrac{7}{8}$

Answer: $\dfrac{35}{48}$

Practice Set A

$\dfrac{2}{3} \cdot 5$

Answer: $\dfrac{10}{3}$

Practice Set A

$(\dfrac{3}{10}) (10)$

Answer: $\dfrac{15}{2}$

Practice Set A

$\dfrac{3}{4} \cdot \dfrac{8}{9} \cdot \dfrac{5}{12}$

Answer: $\dfrac{5}{18}$

Multiplying Fractions by Dividing Out Common Factors

We have seen that to multiply two fractions together, we multiply numerators together, then denominators together, then reduce to lowest terms, if necessary. The reduction can be tedious if the numbers in the fractions are large. For example,

$\dfrac{9}{16} \cdot \dfrac{10}{21} = \dfrac{9 \cdot 10}{16 \cdot 21} = \dfrac{90}{336} = \dfrac{45}{168} = \dfrac{15}{28}$

We avoid the process of reducing if we divide out common factors before we multiply.

$\dfrac{9}{16} \cdot \dfrac{10}{21} = \dfrac{\begin{array} {c} {^3} \\ {\cancel{9}} \end{array}}{\begin{array} {c} {\cancel{16}} \\ {^8} \end{array}} \cdot \dfrac{\begin{array} {c} {^5} \\ {\cancel{10}} \end{array}}{\begin{array} {c} {\cancel{21}} \\ {^7} \end{array}} = \dfrac{3 \cdot 5}{8 \cdot 7} = \dfrac{15}{56}$

Divide 3 into 9 and 21, and divide 2 into 10 and 16. The product is a fraction that is reduced to lowest terms.

How To: The Process of Multiplication by Dividing Out Common Factors

To multiply fractions by dividing out common factors, divide out factors that are common to both a numerator and a denominator. The factor being divided out can appear in any numerator and any denominator.

Sample Set A

Perform the following multiplications.

$\dfrac{4}{5} \cdot \dfrac{5}{6}$

$\dfrac{\begin{array} {c} {^2} \\ {\cancel{4}} \end{array}}{\begin{array} {c} {\cancel{5}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{5}} \end{array}}{\begin{array} {c} {\cancel{6}} \\ {^1} \end{array}} = \dfrac{2 \cdot 1}{1 \cdot 3} = \dfrac{2}{3}$

Divide 4 and 6 by 2
Divide 5 and 5 by 5

Sample Set A

$\dfrac{8}{12} \cdot \dfrac{8}{10}$

$\dfrac{\begin{array} {c} {^4} \\ {\cancel{8}} \end{array}}{\begin{array} {c} {\cancel{12}} \\ {^3} \end{array}} \cdot \dfrac{\begin{array} {c} {^2} \\ {\cancel{8}} \end{array}}{\begin{array} {c} {\cancel{10}} \\ {^5} \end{array}} = \dfrac{4 \cdot 2}{3 \cdot 5} = \dfrac{8}{15}$

Divide 8 and 10 by 2.
Divide 8 and 12 by 4.

Sample Set A

$8 \cdot \dfrac{5}{12} = \dfrac{\begin{array} {c} {^2} \\ {\cancel{8}} \end{array}}{1} \cdot \dfrac{5}{\begin{array} {c} {\cancel{12}} \\ {^3} \end{array}} = \dfrac{2 \cdot 5}{1 \cdot 3} = \dfrac{10}{3}$

Sample Set A

$\dfrac{35}{18} \cdot \dfrac{63}{105}$

$\dfrac{\begin{array} {c} {^{^1}} \\ {^{\cancel{7}}} \\ {\cancel{35}} \end{array}}{\begin{array} {c} {\cancel{18}} \\ {^2} \end{array}} \dfrac{\begin{array} {c} {^7} \\ {\cancel{63}} \end{array}}{\begin{array} {c} {\cancel{105}} \\ {^{\cancel{21}}} \\ {^{^3}} \end{array}} = \dfrac{1 \cdot 7}{2 \cdot 3} = \dfrac{7}{6}$

Sample Set A

$\dfrac{13}{9} \cdot \dfrac{6}{39} \cdot \dfrac{1}{12}$

$\dfrac{\begin{array} {c} {^1} \\ {\cancel{13}} \end{array}}{9} \cdot \dfrac{\begin{array} {c} {^{^1}} \\ {^{\cancel{2}}} \\ {\cancel{6}} \end{array}}{\begin{array} {c} {\cancel{39}} \\ {^{\cancel{3}}} \\ {^{^1}} \end{array}} \cdot \dfrac{1}{\begin{array} {c} {\cancel{12}} \\ {^6} \end{array}} = \dfrac{1 \cdot 1 \cdot 1}{9 \cdot 1 \cdot 6} = \dfrac{1}{54}$

Practice Set B

Perform the following multiplications.

$\dfrac{2}{3} \cdot \dfrac{7}{8}$

Answer: $\dfrac{7}{12}$

Practice Set B

$\dfrac{25}{12} \cdot \dfrac{10}{45}$

Answer: $\dfrac{25}{54}$

Practice Set B

$\dfrac{40}{48} \cdot \dfrac{72}{90}$

Answer: $\dfrac{2}{3}$

Practice Set B

$7 \cdot \dfrac{2}{49}$

Answer: $\dfrac{2}{7}$

Practice Set B

$12 \cdot \dfrac{3}{8}$

Answer: $\dfrac{9}{2}$

Practice Set B

$(\dfrac{13}{7}) (\dfrac{14}{26})$

Answer: 1

Practice Set B

$\dfrac{16}{10} \cdot \dfrac{22}{6} \cdot \dfrac{21}{44}$

Answer: $\dfrac{14}{5}$

Multiplication of Mixed Numbers

Multiplying Mixed Numbers
To perform a multiplication in which there are mixed numbers, it is convenient to first convert each mixed number to an improper fraction, then multiply.

Sample Set C

Perform the following multiplications. Convert improper fractions to mixed numbers.

$1 \dfrac{1}{8} \cdot 4 \dfrac{2}{3}$

Convert each mixed number to an improper fraction.

$1 \dfrac{1}{8} = \dfrac{8 \cdot 1 + 1}{8} = \dfrac{9}{8}$

$4 \dfrac{2}{3} = \dfrac{4 \cdot 3 + 2}{3} = \dfrac{14}{3}$

$\dfrac{\begin{array} {c} {^3} \\ {\cancel{9}} \end{array}}{\begin{array} {c} {\cancel{8}} \\ {^4} \end{array}} \cdot \dfrac{\begin{array} {c} {^7} \\ {\cancel{14}} \end{array}}{\begin{array} {c} {\cancel{3}} \\ {^1} \end{array}} = \dfrac{3 \cdot 7}{4 \cdot 1} = \dfrac{21}{4} = 5 \dfrac{1}{4}$

Sample Set C

$16 \cdot 8 \dfrac{1}{5}$

Convert $8 \dfrac{1}{5}$ to an improper fraction.

$8 \dfrac{1}{5} = \dfrac{5 \cdot 8 + 1}{5} = \dfrac{41}{5}$

$\dfrac{16}{1} \cdot \dfrac{41}{5}$.

There are no common factors to divide out.

$\dfrac{16}{1} \cdot \dfrac{41}{5} = \dfrac{16 \cdot 41}{1 \cdot 5} = \dfrac{656}{5} = 131 \dfrac{1}{5}$

Sample Set C

$9 \dfrac{1}{6} \cdot 12 \dfrac{3}{5}$

Convert to improper fractions.

$9 \dfrac{1}{6} = \dfrac{6 \cdot 9 + 1}{6} = \dfrac{55}{6}$

$12 \dfrac{3}{5} = \dfrac{5 \cdot 12 + 3}{5} = \dfrac{63}{5}$

$\dfrac{\begin{array} {c} {^{11}} \\ {\cancel{55}} \end{array}}{\begin{array} {c} {\cancel{6}} \\ {^2} \end{array}} \cdot \dfrac{\begin{array} {c} {^{21}} \\ {\cancel{63}} \end{array}}{\begin{array} {c} {\cancel{5}} \\ {^1} \end{array}} = \dfrac{11 \cdot 21}{2 \cdot 1} = \dfrac{231}{2} = 115 \dfrac{1}{2}$

Sample Set C

$\begin{array} {rcl} {\dfrac{11}{8} \cdot 4 \dfrac{1}{2} \cdot 3 \dfrac{1}{8}} & = & {\dfrac{11}{8} \cdot \dfrac{\begin{array} {c} {^3} \\ {\cancel{9}} \end{array}}{\begin{array} {c} {\cancel{2}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^5} \\ {\cancel{10}} \end{array}}{\begin{array} {c} {\cancel{3}} \\ {^1} \end{array}}} \\ {} & = & {\dfrac{11 \cdot 3 \cdot 5}{8 \cdot 1 \cdot 1} = \dfrac{165}{8} = 20 \dfrac{5}{8}} \end{array}$

Practice Set C

Perform the following multiplications. Convert improper fractions to mixed numbers.

$2 \dfrac{2}{3} \cdot 2 \dfrac{1}{4}$

Answer: 6

Practice Set C

$6 \dfrac{2}{3} \cdot 3 \dfrac{3}{10}$

Answer: 22

Practice Set C

$7 \dfrac{1}{8} \cdot 12$

Answer: $85\dfrac{1}{2}$

Practice Set C

$2 \dfrac{2}{5} \cdot 3 \dfrac{3}{4} \cdot 3 \dfrac{1}{3}$

Answer: 30

Powers and Roots of Fractions

Sample Set D

Find the value of each of the following.

$(\dfrac{1}{6})^2 = \dfrac{1}{6} \cdot \dfrac{1}{6} = \dfrac{1 \cdot 1}{6 \cdot 6} = \dfrac{1}{36}$

Sample Set D

$\sqrt{\dfrac{9}{100}}$. We’re looking for a number, call it ?, such that when it is squared, $\dfrac{9}{100}$ is produced.

$(?)^2 = \dfrac{9}{100}$

We know that

$3^2 = 9$ and $10^2 = 100$

We'll try $\dfrac{3}{10}$. Since

$(\dfrac{3}{10})^2 = \dfrac{3}{10} \cdot \dfrac{3}{10} = \dfrac{3 \cdot 3}{10 \cdot 10} = \dfrac{9}{100}$

$\sqrt{\dfrac{9}{100}} = \dfrac{3}{10}$

Sample Set D

$4\dfrac{2}{5} \cdot \sqrt{\dfrac{100}{121}}$

$\dfrac{\begin{array} {c} {^2} \\ {\cancel{22}} \end{array}}{\begin{array} {c} {\cancel{5}} \\ {^1} \end{array}} \cdot \dfrac{^2}{\cancel{10}} = \dfrac{\begin{array} {c} {\cancel{11}} \\ {^1} \end{array}}{\begin{array} {c} {} \\ {} \end{array}} = \dfrac{4}{1} = 4$

$4 \dfrac{2}{5} \cdot \sqrt{\dfrac{100}{121}} = 4$

Practice Set D

Find the value of each of the following.

$(\dfrac{1}{8})^2$

Answer: $\dfrac{1}{64}$

Practice Set D

$(\dfrac{3}{10})^2$

Answer: $\dfrac{9}{100}$

Practice Set D

$\sqrt{\dfrac{4}{9}}$

Answer: $\dfrac{2}{3}$

Practice Set D

$\sqrt{\dfrac{1}{4}}$

Answer: $\dfrac{1}{2}$

Practice Set D

$\dfrac{3}{8} \cdot \sqrt{\dfrac{1}{9}}$

Answer: $\dfrac{1}{8}$

Practice Set D

$9 \dfrac{1}{3} \cdot \sqrt{\dfrac{81}{100}}$

Answer: $8 \dfrac{2}{5}$

Practice Set D

$2 \dfrac{8}{13} \cdot \sqrt{\dfrac{169}{16}}$

Answer: $8 \dfrac{1}{2}$

Exercises

For the following six problems, use the diagrams to find each of the following parts. Use multiplication to verify your result.

Exercise $\PageIndex{1}$

$\dfrac{3}{4}$ of $\dfrac{1}{3}$

$A rectangle divided into twelve parts in a pattern of four rows and three columns.$

Answer

$\dfrac{1}{4}$

$A rectangle divided into twelve parts in a pattern of four rows and three columns. Three of the parts are shaded.$

Exercise $\PageIndex{2}$

$\dfrac{2}{3}$ of $\dfrac{3}{5}$

$A rectangle divided into twelve parts in a pattern of three rows and four columns.$

Exercise $\PageIndex{3}$

$\dfrac{2}{7}$ of $\dfrac{7}{8}$

$A rectangle divided into fifty-six parts in a pattern of seven rows and eight columns.$

Answer

$\dfrac{1}{4}$

$A rectangle divided into fifty-six parts in a pattern of seven rows and eight columns. Fourteen of the parts are shaded.$

Exercise $\PageIndex{4}$

$\dfrac{5}{6}$ of $\dfrac{3}{4}$

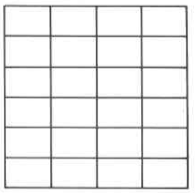
$A rectangle divided into twenty-four parts in a pattern of six rows and four columns.$

Exercise $\PageIndex{5}$

$\dfrac{1}{8}$ of $\dfrac{1}{8}$

$A rectangle divided into sixty-four parts in a pattern of eight rows and eight columns.$

Answer

$\dfrac{1}{64}$

$A rectangle divided into sixty-four parts in a pattern of eight rows and eight columns. One part is shaded.$

Exercise $\PageIndex{6}$

$\dfrac{7}{12}$ of $\dfrac{6}{7}$

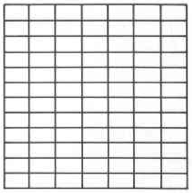
$A rectangle divided into eighty-four parts in a pattern of twelve rows and seven columns.$

For the following problems, find each part without using a diagram.

Exercise $\PageIndex{7}$

$\dfrac{1}{2}$ of $\dfrac{4}{5}$

Answer: $\dfrac{2}{5}$

Exercise $\PageIndex{8}$

$\dfrac{3}{5}$ of $\dfrac{5}{12}$

Exercise $\PageIndex{9}$

$\dfrac{1}{4}$ of $\dfrac{8}{9}$

Answer: $\dfrac{2}{9}$

Exercise $\PageIndex{10}$

$\dfrac{3}{16}$ of $\dfrac{12}{15}$

Exercise $\PageIndex{11}$

$\dfrac{2}{9}$ of $\dfrac{6}{5}$

Answer: $\dfrac{4}{15}$

Exercise $\PageIndex{12}$

$\dfrac{1}{8}$ of $\dfrac{3}{8}$

Exercise $\PageIndex{13}$

$\dfrac{2}{3}$ of $\dfrac{9}{10}$

Answer: $\dfrac{3}{5}$

Exercise $\PageIndex{14}$

$\dfrac{18}{19}$ of $\dfrac{38}{54}$

Exercise $\PageIndex{15}$

$\dfrac{5}{6}$ of $2 \dfrac{2}{5}$

Answer: 2

Exercise $\PageIndex{16}$

$\dfrac{3}{4}$ of $3 \dfrac{3}{5}$

Exercise $\PageIndex{17}$

$\dfrac{3}{2}$ of $2 \dfrac{2}{9}$

Answer: $\dfrac{10}{3}$ or $3 \dfrac{1}{3}$

Exercise $\PageIndex{18}$

$\dfrac{15}{4}$ of $4 \dfrac{4}{5}$

Exercise $\PageIndex{19}$

$5 \dfrac{1}{3}$ of $9 \dfrac{3}{4}$

Answer: 52

Exercise $\PageIndex{20}$

$1 \dfrac{13}{15}$ of $8 \dfrac{3}{4}$

Exercise $\PageIndex{21}$

$\dfrac{8}{9}$ of $\dfrac{3}{4}$ of $\dfrac{2}{3}$

Answer: $\dfrac{4}{9}$

Exercise $\PageIndex{22}$

$\dfrac{1}{6}$ of $\dfrac{12}{13}$ of $\dfrac{26}{36}$

Exercise $\PageIndex{23}$

$\dfrac{1}{2}$ of $\dfrac{1}{3}$ of $\dfrac{1}{4}$

Answer: $\dfrac{1}{24}$

Exercise $\PageIndex{24}$

$1 \dfrac{3}{7}$ of $5 \dfrac{1}{5}$ of $8 \dfrac{1}{3}$

Exercise $\PageIndex{25}$

$2 \dfrac{4}{5}$ of $5 \dfrac{5}{6}$ of $7 \dfrac{5}{7}$

Answer: 126

For the following problems, find the products. Be sure to reduce.

Exercise $\PageIndex{26}$

$\dfrac{1}{3} \cdot \dfrac{2}{3}$

Exercise $\PageIndex{27}$

$\dfrac{1}{2} \cdot \dfrac{1}{2}$

Answer: $\dfrac{1}{4}$

Exercise $\PageIndex{28}$

$\dfrac{3}{4} \cdot \dfrac{3}{8}$

Exercise $\PageIndex{29}$

$\dfrac{2}{5} \cdot \dfrac{5}{6}$

Answer: $\dfrac{1}{3}$

Exercise $\PageIndex{30}$

$\dfrac{3}{8} \cdot \dfrac{8}{9}$

Exercise $\PageIndex{31}$

$\dfrac{5}{6} \cdot \dfrac{14}{15}$

Answer: $\dfrac{7}{9}$

Exercise $\PageIndex{32}$

$\dfrac{4}{7} \cdot \dfrac{7}{4}$

Exercise $\PageIndex{33}$

$\dfrac{3}{11} \cdot \dfrac{11}{3}$

Answer: 1

Exercise $\PageIndex{34}$

$\dfrac{9}{16} \cdot \dfrac{20}{27}$

Exercise $\PageIndex{35}$

$\dfrac{35}{36} \cdot \dfrac{48}{55}$

Answer: $\dfrac{28}{33}$

Exercise $\PageIndex{36}$

$\dfrac{21}{25} \cdot \dfrac{15}{14}$

Exercise $\PageIndex{37}$

$\dfrac{76}{99} \cdot \dfrac{66}{38}$

Answer: $\dfrac{4}{3}$

Exercise $\PageIndex{38}$

$\dfrac{3}{7} \cdot \dfrac{14}{18} \cdot \dfrac{6}{2}$

Exercise $\PageIndex{39}$

$\dfrac{4}{15} \cdot \dfrac{10}{3} \cdot \dfrac{27}{2}$

Answer: 12

Exercise $\PageIndex{40}$

$\dfrac{14}{15} \cdot \dfrac{21}{28} \cdot \dfrac{45}{7}$

Exercise $\PageIndex{41}$

$\dfrac{8}{3} \cdot \dfrac{15}{4} \cdot \dfrac{16}{21}$

Answer: $7\dfrac{13}{21}$ or $\dfrac{160}{21}$

Exercise $\PageIndex{42}$

$\dfrac{18}{14} \cdot \dfrac{21}{35} \cdot \dfrac{36}{7}$

Exercise $\PageIndex{43}$

$\dfrac{3}{5} \cdot 20$

Answer: 12

Exercise $\PageIndex{44}$

$\dfrac{8}{9} \cdot 18$

Exercise $\PageIndex{45}$

$\dfrac{6}{11} \cdot 33$

Answer: 18

Exercise $\PageIndex{46}$

$\dfrac{18}{19} \cdot 38$

Exercise $\PageIndex{47}$

$\dfrac{5}{6} \cdot 10$

Answer: $\dfrac{25}{3}$ or $8\dfrac{1}{3}$

Exercise $\PageIndex{48}$

$\dfrac{1}{9} \cdot 3$

Exercise $\PageIndex{49}$

$5 \cdot \dfrac{3}{8}$

Answer: $\dfrac{15}{8} =1 \dfrac{7}{8}$

Exercise $\PageIndex{50}$

$16 \cdot \dfrac{1}{4}$

Exercise $\PageIndex{51}$

$\dfrac{2}{3} \cdot 12 \cdot \dfrac{3}{4}$

Answer: 6

Exercise $\PageIndex{52}$

$\dfrac{3}{8} \cdot 24 \cdot \dfrac{2}{3}$

Exercise $\PageIndex{53}$

$\dfrac{5}{18} \cdot 10 \cdot \dfrac{2}{5}$

Answer: $\dfrac{10}{9} = 1 \dfrac{1}{9}$

Exercise $\PageIndex{54}$

$\dfrac{16}{15} \cdot 50 \cdot \dfrac{3}{10}$

Exercise $\PageIndex{55}$

$5 \dfrac{1}{3} \cdot \dfrac{27}{32}$

Answer: $\dfrac{9}{2} = 4 \drac{1}{2}$

Exercise $\PageIndex{56}$

$2 \dfrac{6}{7} \cdot 5 \dfrac{3}{5}$

Exercise $\PageIndex{57}$

$6 \dfrac{1}{4} \cdot 2 \dfrac{4}{15}$

Answer: $\dfrac{85}{6} = 14 \drac{1}{6}$

Exercise $\PageIndex{58}$

$9\dfrac{1}{3} \cdot \dfrac{9}{16} \cdot 1 \dfrac{1}{3}$

Exercise $\PageIndex{59}$

$3 \dfrac{5}{9} \cdot 1 \dfrac{13}{14} \cdot 10 \dfrac{1}{2}$

Answer: 72

Exercise $\PageIndex{60}$

$20 \dfrac{1}{4} \cdot 8 \dfrac{2}{3} \cdot 16 \dfrac{4}{5}$

Exercise $\PageIndex{61}$

$(\dfrac{2}{3})^2$

Answer: $\dfrac{4}{9}$

Exercise $\PageIndex{62}$

$(\dfrac{3}{8})^2$

Exercise $\PageIndex{63}$

$(\dfrac{2}{11})^2$

Answer: $\dfrac{4}{121}$

Exercise $\PageIndex{64}$

$(\dfrac{8}{9})^2$

Exercise $\PageIndex{65}$

$(\dfrac{1}{2})^2$

Answer: $\dfrac{1}{4}$

Exercise $\PageIndex{66}$

$(\dfrac{3}{5})^2 \cdot \dfrac{20}{3}$

Exercise $\PageIndex{67}$

$(\dfrac{1}{4})^2 \cdot \dfrac{16}{15}$

Answer: $\dfrac{1}{15}$

Exercise $\PageIndex{68}$

$(\dfrac{1}{2})^2 \cdot \dfrac{8}{9}$

Exercise $\PageIndex{69}$

$(\dfrac{1}{2})^2 \cdot (\dfrac{2}{5})^2$

Answer: $\dfrac{1}{25}$

Exercise $\PageIndex{70}$

$(\dfrac{3}{7})^2 \cdot (\dfrac{1}{9})^2$

For the following problems, find each value. Reduce answers to lowest terms or convert to mixed numbers.

Exercise $\PageIndex{71}$

$\sqrt{\dfrac{4}{9}}$

Answer: $\dfrac{2}{3}$

Exercise $\PageIndex{72}$

$\sqrt{\dfrac{16}{25}}$

Exercise $\PageIndex{73}$

$\sqrt{\dfrac{81}{121}}$

Answer: $\dfrac{9}{11}$

Exercise $\PageIndex{74}$

$\sqrt{\dfrac{36}{49}}$

Exercise $\PageIndex{75}$

$\sqrt{\dfrac{144}{25}}$

Answer: $\dfrac{12}{5} = 2 \dfrac{2}{5}$

Exercise $\PageIndex{76}$

$\dfrac{2}{3} \cdot \sqrt{\dfrac{9}{16}}$

Exercise $\PageIndex{77}$

$\dfrac{3}{5} \cdot \sqrt{\dfrac{25}{81}}$

Answer: $\dfrac{1}{3}$

Exercise $\PageIndex{78}$

$(\dfrac{8}{5})^2 \cdot \sqrt{\dfrac{25}{64}}$

Exercise $\PageIndex{79}$

$(1 \dfrac{3}{4})^2 \cdot \sqrt{\dfrac{4}{49}}$

Answer: $\dfrac{7}{8}$

Exercise $\PageIndex{80}$

$(2 \dfrac{2}{3})^2 \cdot \sqrt{\dfrac{36}{49}} \cdot \sqrt{\dfrac{64}{81}}$

Exercises for Review

Exercise $\PageIndex{81}$

How many thousands in 342,810?

Answer: 2

Exercise $\PageIndex{82}$

Find the sum of 22, 42, and 101.

Exercise $\PageIndex{83}$

Is 634,281 divisible by 3?

Answer: yes

Exercise $\PageIndex{84}$

Is the whole number 51 prime or composite?

Exercise $\PageIndex{85}$

Reduce $\dfrac{36}{150}$ to lowest terms

Answer: $\dfrac{6}{25}$

Search

Text Color

Text Size

Margin Size

Font Type

Sample Set A

Sample Set A

Sample Set A

How To: The Process of Multiplication by Dividing Out Common Factors

Sample Set A

Sample Set A

Sample Set A

Sample Set A

Sample Set A

Sample Set C

Sample Set C

Sample Set C

Sample Set C

Sample Set D

Sample Set D

Sample Set D