4.5: Division of Fractions

Last updated
Save as PDF

Page ID: 48854

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Learning Objectives

be able to determine the reciprocal of a number
be able to divide one fraction by another

Reciprocals

Definition: Reciprocals

Two numbers whose product is 1 are called reciprocals of each other.

Sample Set A

The following pairs of numbers are reciprocals.

$\underbrace{\dfrac{3}{4} \text{and} \dfrac{4}{3}}_{\dfrac{3}{4} \cdot \dfrac{4}{3} = 1}$

Sample Set A

$\underbrace{\dfrac{7}{16} \text{and} \dfrac{16}{7}}_{\dfrac{7}{16} \cdot \dfrac{16}{7} = 1}$

Sample Set A

$\underbrace{\dfrac{1}{6} \text{and} \dfrac{6}{1}}_{\dfrac{1}{6} \cdot \dfrac{6}{1} = 1}$

Notice that we can find the reciprocal of a nonzero number in fractional form by inverting it (exchanging positions of the numerator and denominator).

Practice Set A

Find the reciprocal of each number.

$\dfrac{3}{10}$

Answer: $\dfrac{10}{3}$

Practice Set A

$\dfrac{2}{3}$

Answer: $\dfrac{3}{2}$

Practice Set A

$\dfrac{7}{8}$

Answer: $\dfrac{8}{7}$

Practice Set A

$\dfrac{1}{5}$

Answer: 5

Practice Set A

$2 \dfrac{2}{7}$

Hint

Write this number as an improper fraction first.

Answer: $\dfrac{7}{16}$

Practice Set A

$5 \dfrac{1}{4}$

Answer: $\dfrac{4}{21}$

Practice Set A

$10 \dfrac{3}{16}$

Answer: $\dfrac{16}{163}$

Dividing Fractions

Our concept of division is that it indicates how many times one quantity is contained in another quantity. For example, using the diagram we can see that there are 6 one-thirds in 2.

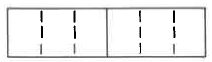
$Two rectangles, each divided into three parts. The rectangles are connected to each other.$

There are 6 one-thirds in 2.

Since 2 contains six $\dfrac{1}{3}$'s we express this as

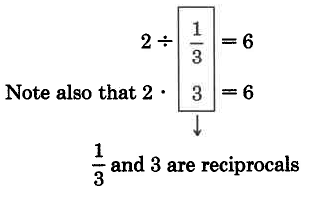
$Two divided by one-third is equal to six. Note also that two times three is equal to six, because one-third and three are reciprocals.$

Using these observations, we can suggest the following method for dividing a number by a fraction.

Dividing One Fraction by Another Fraction
To divide a first fraction by a second, nonzero fraction, multiply the first traction by the reciprocal of the second fraction.

Invert and Multiply
This method is commonly referred to as "invert the divisor and multiply."

Sample Set B

Perform the following divisions.

$\dfrac{1}{2} \div \dfrac{3}{4}$. The divisor is $\dfrac{3}{4}$. Its reciprocal is $\dfrac{4}{3}$. Multiply $\dfrac{1}{3}$ by $\dfrac{4}{3}$.

$\dfrac{1}{3} \cdot \dfrac{4}{3} = \dfrac{1 \cdot 4}{3 \cdot 3} = \dfrac{4}{9}$

$\dfrac{1}{2} \div \dfrac{3}{4} = \dfrac{4}{9}$

Sample Set B

$\dfrac{3}{8} \div \dfrac{5}{4}$. The divisor is $\dfrac{5}{4}$. Its reciprocal is $\dfrac{4}{5}$. Multiply $\dfrac{3}{8}$ by $\dfrac{4}{5}$.

$\dfrac{3}{\begin{array} {c} {\cancel{8}} \\ {^2} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{4}} \end{array}}{5} = \dfrac{3 \cdot 1}{2 \cdot 5} = \dfrac{3}{10}$

$\dfrac{3}{8} \div \dfrac{5}{4} = \dfrac{3}{10}$

Sample Set B

$\dfrac{5}{6} \div \dfrac{5}{12}$. The divisor is $\dfrac{5}{12}$. Its reciprocal is $\dfrac{12}{5}$. Multiply $\dfrac{5}{6}$ by $\dfrac{12}{5}$.

$\dfrac{\begin{array} {c} {^1} \\ {\cancel{5}} \end{array}}{\begin{array} {c} {\cancel{6}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^2} \\ {\cancel{12}} \end{array}}{\begin{array} {c} {\cancel{5}} \\ {^1} \end{array}} = \dfrac{1 \cdot 2}{1 \cdot 1} = \dfrac{2}{1} = 2$

$\dfrac{5}{6} \div \dfrac{5}{12} = 2$

Sample Set B

$2 \dfrac{2}{9} \div 3 \dfrac{1}{3}$. Convert each mixed number to an improper fraction.

$2 \dfrac{2}{9} = \dfrac{9 \cdot 2 + 2}{9} = \dfrac{20}{9}$.

$3 \dfrac{1}{3} = \dfrac{3 \cdot 3 + 1}{3} = \dfrac{10}{3}$.

$\dfrac{20}{9} \div \dfrac{10}{3}$ The divisor is $\dfrac{10}{3}$. Its reciprocal is $\dfrac{3}{10}$. Multiply $\dfrac{20}{9}$ by $\dfrac{3}{10}$.

$\dfrac{\begin{array} {c} {^2} \\ {\cancel{20}} \end{array}}{\begin{array} {c} {\cancel{9}} \\ {^3} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{3}} \end{array}}{\begin{array} {c} {\cancel{10}} \\ {^1} \end{array}} = \dfrac{2 \cdot 1}{3 \cdot 1} = \dfrac{2}{3}$

$2 \dfrac{2}{9} \div 3 \dfrac{1}{3} = \dfrac{2}{3}$

Sample Set B

$\dfrac{12}{11} \div 8$. First conveniently write 8 as $\dfrac{8}{1}$.

$\dfrac{12}{11} \div \dfrac{8}{1}$. The divisor is $\dfrac{8}{1}$. Its reciprocal is $\dfrac{1}{8}$. Multiply $\dfrac{12}{11}$ by $\dfrac{1}{8}$.

$\dfrac{\begin{array} {c} {^3} \\ {\cancel{12}} \end{array}}{11} \cdot \dfrac{1}{\begin{array} {c} {\cancel{8}} \\ {^2} \end{array}} = \dfrac{3 \cdot 1}{11 \cdot 2} = \dfrac{3}{22}$

$\dfrac{12}{11} \div 8 = \dfrac{3}{22}$

Sample Set B

$\dfrac{7}{8} \div \dfrac{21}{20} \cdot \dfrac{3}{35}$. The divisor is $\dfrac{21}{20}$. Its reciprocal is $\dfrac{20}{21}$.

$\dfrac{\begin{array} {c} {^1} \\ {\cancel{7}} \end{array}}{\begin{array} {c} {\cancel{8}} \\ {^2} \end{array}} \cdot \dfrac{\begin{array} {c} {^{^1}} \\ {^{\cancel{5}}} \\ {\cancel{20}} \end{array}}{\begin{array} {c} {\cancel{21}} \\ {^{\cancel{3}}} \\ {^{^1}} \end{array}} \dfrac{\begin{array} {c} {^1} \\ {\cancel{3}} \end{array}}{\begin{array} {c} {\cancel{35}} \\ {^7} \end{array}} = \dfrac{1 \cdot 1 \cdot 1}{2 \cdot 1 \cdot 7} = \dfrac{1}{14}$

$\dfrac{7}{8} \div \dfrac{21}{20} \cdot \dfrac{3}{25} = \dfrac{1}{14}$

Sample Set B

How many $2 \dfrac{3}{8}$ inch-wide packages can be placed in a box 19 inches wide?

The problem is to determine how many two and three eighths are contained in 19, that is, what is $19 \div 2 \dfrac{3}{8}$?

$2\dfrac{3}{8} = \dfrac{19}{8}$ Convert the divisor $2 \dfrac{3}{8}$ to an improper fraction.

$19 = \dfrac{19}{1}$ Write the dividend 19 as $\dfrac{19}{1}$.

$\dfrac{19}{1} \div \dfrac{19}{8}$ The divisor is $\dfrac{19}{8}$. Its reciprocal is $\dfrac{8}{19}$.

$\dfrac{\begin{array} {c} {^1} \\ {\cancel{19}} \end{array}}{1} \cdot \dfrac{8}{\begin{array} {c} {\cancel{19}} \\ {^1} \end{array}} = \dfrac{1 \cdot 8}{1 \cdot 1} = \dfrac{8}{1} = 8$

Thus, 8 packages will fit into the box.

Practice Set B

Perform the following divisions.

$\dfrac{1}{2} \div \dfrac{9}{8}$

Answer: $\dfrac{4}{9}$

Practice Set B

$\dfrac{3}{8} \div \dfrac{9}{24}$

Answer: 1

Practice Set B

$\dfrac{7}{15} \div \dfrac{14}{15}$

Answer: $\dfrac{1}{2}$

Practice Set B

$8 \div \dfrac{8}{15}$

Answer: 15

Practice Set B

$6 \dfrac{1}{4} \div \dfrac{5}{12}$

Answer: 15

Practice Set B

$3 \dfrac{1}{3} \div 1 \dfrac{2}{3}$

Answer: 2

Practice Set B

$\dfrac{5}{6} \div \dfrac{2}{3} \cdot \dfrac{8}{25}$

Answer: $\dfrac{2}{5}$

Practice Set B

A container will hold 106 ounces of grape juice. How many $6 \dfrac{5}{8}$ -ounce glasses of grape juice can be served from this container?

Answer: 16 glasses

Determine each of the following quotients and then write a rule for this type of division.

Practice Set B

$1 \div \dfrac{2}{3}$

Answer: $\dfrac{3}{2}$

Practice Set B

$1 \div \dfrac{3}{8}$

Answer: $\dfrac{8}{3}$

Practice Set B

$1 \div \dfrac{3}{4}$

Answer: $\dfrac{4}{3}$

Practice Set B

$1 \div \dfrac{5}{2}$

Answer: $\dfrac{2}{5}$

Practice Set B

When dividing 1 by a fraction, the quotient is the .

Answer: is the reciprocal of the fraction.

Exercises

For the following problems, find the reciprocal of each number.

Exercise $\PageIndex{1}$

$\dfrac{4}{5}$

Answer: $\dfrac{5}{4}$ or $1 \dfrac{1}{4}$

Exercise $\PageIndex{2}$

$\dfrac{8}{11}$

Exercise $\PageIndex{3}$

$\dfrac{2}{9}$

Answer: $\dfrac{9}{2}$ or $4 \dfrac{1}{2}$

Exercise $\PageIndex{4}$

$\dfrac{1}{5}$

Exercise $\PageIndex{5}$

$3\dfrac{1}{4}$

Answer: $\dfrac{4}{13}$

Exercise $\PageIndex{6}$

$8 \dfrac{1}{4}$

Exercise $\PageIndex{7}$

$3\dfrac{2}{7}$

Answer: $\dfrac{7}{23}$

Exercise $\PageIndex{8}$

$5 \dfrac{3}{4}$

Exercise $\PageIndex{9}$

Answer: 1

Exercise $\PageIndex{10}$

For the following problems, find each value.

Exercise $\PageIndex{11}$

$\dfrac{3}{8} \div \dfrac{3}{5}$

Answer: $\dfrac{5}{8}$

Exercise $\PageIndex{12}$

$\dfrac{5}{9} \div \dfrac{5}{6}$

Exercise $\PageIndex{13}$

$\dfrac{9}{16} \div \dfrac{15}{8}$

Answer: $\dfrac{3}{10}$

Exercise $\PageIndex{14}$

$\dfrac{4}{9} \div \dfrac{6}{15}$

Exercise $\PageIndex{15}$

$\dfrac{25}{49} \div \dfrac{4}{9}$

Answer: $\dfrac{225}{196}$ or $1 \dfrac{29}{196}$

Exercise $\PageIndex{16}$

$\dfrac{15}{4} \div \dfrac{27}{8}$

Exercise $\PageIndex{17}$

$\dfrac{24}{75} \div \dfrac{8}{15}$

Answer: $\dfrac{3}{5}$

Exercise $\PageIndex{18}$

$\dfrac{5}{7} \div 0$

Exercise $\PageIndex{19}$

$\dfrac{7}{8} \div \dfrac{7}{8}$

Answer: 1

Exercise $\PageIndex{20}$

$0 \div \dfrac{3}{5}$

Exercise $\PageIndex{21}$

$\dfrac{4}{11} \div \dfrac{4}{11}$

Answer: 1

Exercise $\PageIndex{22}$

$\dfrac{2}{3} \div \dfrac{2}{3}$

Exercise $\PageIndex{23}$

$\dfrac{7}{10} \div \dfrac{10}{7}$

Answer: $\dfrac{49}{100}$

Exercise $\PageIndex{24}$

$\dfrac{3}{4} \div 6$

Exercise $\PageIndex{25}$

$\dfrac{9}{5} \div 3$

Answer: $\dfrac{3}{5}$

Exercise $\PageIndex{26}$

$4 \dfrac{1}{6} \div 3 \dfrac{1}{3}$

Exercise $\PageIndex{27}$

$7 \dfrac{1}{7} \div 8 \dfrac{1}{3}$

Answer: $\dfrac{6}{7}$

Exercise $\PageIndex{28}$

$1 \dfrac{1}{2} \div 1 \dfrac{1}{5}$

Exercise $\PageIndex{29}$

$3 \dfrac{2}{5} \div \dfrac{6}{25}$

Answer: $\dfrac{85}{6}$ or $14 \dfrac{1}{6}$

Exercise $\PageIndex{30}$

$5 \dfrac{1}{6} \div \dfrac{31}{6}$

Exercise $\PageIndex{31}$

$\dfrac{35}{6} \div 3 \dfrac{3}{4}$

Answer: $\dfrac{28}{18} = \dfrac{14}{9}$ or $1 \dfrac{5}{9}$

Exercise $\PageIndex{32}$

$5 \dfrac{1}{9} \div \dfrac{1}{18}$

Exercise $\PageIndex{33}$

$8 \dfrac{3}{4} \div \dfrac{7}{8}$

Answer: 10

Exercise $\PageIndex{34}$

$\dfrac{12}{8} \div 1 \dfrac{1}{2}$

Exercise $\PageIndex{35}$

$3 \dfrac{1}{8} \div \dfrac{15}{16}$

Answer: $\dfrac{10}{3}$ or $3 \dfrac{1}{3}$

Exercise $\PageIndex{36}$

$11 \dfrac{11}{12} \div 9 \dfrac{5}{8}$

Exercise $\PageIndex{37}$

$2 \dfrac{2}{9} \div 11 \dfrac{2}{3}$

Answer: $\dfrac{4}{21}$

Exercise $\PageIndex{38}$

$\dfrac{16}{3} \div 6 \dfrac{2}{5}$

Exercise $\PageIndex{39}$

$4 \dfrac{3}{25} \div 2 \dfrac{56}{75}$

Answer: $\dfrac{3}{2}$ or $1 \dfrac{1}{2}$

Exercise $\PageIndex{40}$

$\dfrac{1}{1000} \div \dfrac{1}{100}$

Exercise $\PageIndex{41}$

$\dfrac{3}{8} \div \dfrac{9}{16} \cdot \dfrac{6}{5}$

Answer: $\dfrac{4}{5}$

Exercise $\PageIndex{42}$

$\dfrac{3}{16} \cdot \dfrac{9}{8} \cdot \dfrac{6}{5}$

Exercise $\PageIndex{43}$

$\dfrac{4}{15} \div \dfrac{2}{25} \cdot \dfrac{9}{10}$

Answer: 3

Exercise $\PageIndex{44}$

$\dfrac{21}{30} \cdot 1 \dfrac{1}{4} \div \dfrac{9}{10}$

Exercise $\PageIndex{45}$

$8 \dfrac{1}{3} \cdot \dfrac{36}{75} \div 4$

Answer: 1

Exercises for Review

Exercise $\PageIndex{46}$

What is the value of 5 in the number 504,216?

Exercise $\PageIndex{47}$

Find the product of 2,010 and 160.

Answer: 321,600

Exercise $\PageIndex{48}$

Use the numbers 8 and 5 to illustrate the commutative property of multiplication.

Exercise $\PageIndex{49}$

Find the least common multiple of 6, 16, and 72.

Answer: 144

Exercise $\PageIndex{50}$

Find $\dfrac{8}{9}$ of $6 \dfrac{3}{4}$

Search

Text Color

Text Size

Margin Size

Font Type