4.6: Applications Involving Fractions

Last updated
Save as PDF

Page ID: 48855

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Learning Objectives

be able to solve missing product statements
be able to solve missing factor statements

Multiplication Statements

Statement, Multiplication Statement
A statement is a sentence that is either true or false. A mathematical statement of the form

product = (factor 1) ⋅ (factor 2)

is a multiplication statement. Depending on the numbers that are used, it can be either true or false.

Omitting exactly one of the three numbers in the statement will produce exactly one of the following three problems. For convenience, we'll represent the omitted (or missing) number with the letter M (M for Missing).

M = (factor 1) ⋅ (factor 2) Missing product statement.
M ⋅ (factor 2) = product Missing factor statement.
(factor 1) ⋅ M = product Missing factor statement.

We are interested in developing and working with methods to determine the missing number that makes the statement true. Fundamental to these methods is the ability to translate two words to mathematical symbols. The word

of translates to times
is translates to equals

Missing Products Statements

The equation $M = 8 \cdot 4$ is a missing product statement. We can find the value of M that makes this statement true by multiplyingthe known factors.

Missing product statements can be used to determine the answer to a question such as, "What number is fraction 1 of fraction 2?

Sample Set A

Find $\dfrac{3}{4}$ of $\dfrac{8}{9}$. We are being asked the question, "What number is $\dfrac{3}{4}$ of $\dfrac{8}{9}$?" We must translate from words to mathematical symbols.

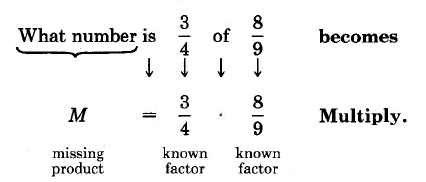
$Two statements in a row. Each element is aligned with something above it. First, what number is three-fourths of eight-ninths, becomes. Second, M equals three-fourths times eight-ninths, multiply. M is the missing product, and three-fourths and eight-ninths are known factors.$

$M = \dfrac{\begin{array} {c} {^1} \\ {\cancel{3}} \end{array}}{\begin{array} {c} {\cancel{4}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^2} \\ {\cancel{8}} \end{array}}{\begin{array} {c} {\cancel{9}} \\ {^3} \end{array}} = \dfrac{1 \cdot 2}{1 \cdot 3} = \dfrac{2}{3}$

Thus, $\dfrac{3}{4}$ of $\dfrac{8}{9}$ is $\dfrac{2}{3}$.

$Two statements in a row. Each element is aligned with something above it. First, what number is three-fourths of twenty-four. Second, M equals three-fourths times twenty-four. M is the missing product, and three-fourths and eight-ninths are known factors.$

$M = \dfrac{3}{\begin{array} {c} {\cancel{4}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^6} \\ {\cancel{24}} \end{array}}{1} = \dfrac{3 \cdot 6}{1 \cdot 1} = \dfrac{18}{1} = 18$

Thus, 18 is $\dfrac{3}{4}$ of 24.

Practice Set A

Find $\dfrac{3}{8}$ of $\dfrac{16}{15}$.

Answer: $\dfrac{2}{5}$

Practice Set A

What number is $\dfrac{9}{10}$ of $\dfrac{5}{6}$?

Answer: $\dfrac{3}{4}$

Practice Set A

$\dfrac{11}{16}$ of $\dfrac{8}{33}$ is what number?

Answer: $\dfrac{1}{6}$

Missing Factor Statements

The equation $8 \cdot M = 32$ is a missing factor statement. We can find the value of $M$ that makes this statement true by dividing (since we know that $32 \div 8 = 4$.

$The expression 8 times M equals 32 means that M equals thirty-two divided by eight. M is the missing factor, thirty-two is the product, and eight is the known factor.$

Finding the Missing Factor
To find the missing factor in a missing factor statement, divide the product by the known factor.
missing factor = (product) $\div$ (known factor)

Missing factor statements can be used to answer such questions as

$\dfrac{3}{8}$ of what number is $\dfrac{9}{4}$?
What part of $1 \dfrac{2}{7}$ is $1 \dfrac{13}{14}$?

Sample Set B

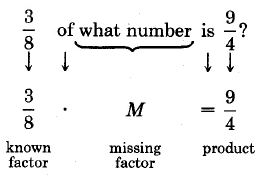
$Three eighths of what number is nine fourths? This is the same as three eighths times M equals nine fourths. Three eighths is the known factor, M is the missing factor, and nine-fourths is the product.$

Now, using

missing factor = (product) $\div$ (known factor)

We get

$\begin{array} {rcl} {M = \dfrac{9}{4} \div \dfrac{3}{8} = \dfrac{9}{4} \cdot \dfrac{8}{3}} & = & {\dfrac{\begin{array} {c} {^3} \\ {\cancel{9}} \end{array}}{\begin{array} {c} {\cancel{4}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^2} \\ {\cancel{8}} \end{array}}{\begin{array} {c} {\cancel{3}} \\ {^1} \end{array}}} \\ {} & = & {\dfrac{3 \cdot 2}{1 \cdot 1}} \\ {} & = & {6} \end{array}$

$Check the work: is three eighths times six equal to nine fourths? Cancel out the six and the eight by dividing each by two. This can be simplified to find out that yes, they are equal.$

Thus, $\dfrac{3}{8}$ of 6 is $\dfrac{9}{4}$.

$What part of 1 and two-sevenths is 1 and thirteen-fourteenths? This is equivalent to M times 1 and two-sevenths equals 1 and thirteen-fourteenths. M is the missing factor, 1 and two-sevenths is the known factor, and 1 and thirteen-fourteenths is the product.$

For convenience, let's convert the mixed numbers to improper fractions.

$M \cdot \dfrac{9}{7} = \dfrac{27}{14}$

Now, using

missing factor = (product) $\div$ (known factor)

we get

$\begin{array} {rcl} {M = \dfrac{27}{14} \div \dfrac{9}{7} = \dfrac{27}{14} \cdot \dfrac{7}{9}} & = & {\dfrac{\begin{array} {c} {^3} \\ {\cancel{27}} \end{array}}{\begin{array} {c} {\cancel{14}} \\ {^2} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{7}} \end{array}}{\begin{array} {c} {\cancel{9}} \\ {^1} \end{array}}} \\ {} & = & {\dfrac{3 \cdot 1}{2 \cdot 1}} \\ {} & = & {\dfrac{3}{2}} \end{array}$

$Check: is three halves times nine sevenths equal to twenty-seven fourteenths? Yes.$

Thus, $\dfrac{3}{2}$ of $1 \dfrac{2}{7}$ is $1 \dfrac{13}{14}$.

Practice Set B

$\dfrac{3}{5}$ of what number is $\dfrac{9}{20}$?

Answer: $\dfrac{3}{4}$

Practice Set B

$3 \dfrac{3}{4}$ of what number is $2 \dfrac{2}{9}$?

Answer: $\dfrac{16}{27}$

Practice Set B

What part of $\dfrac{3}{5}$ is $\dfrac{9}{10}$?

Answer: $1 \dfrac{1}{2}$

Practice Set B

What part of $1 \dfrac{1}{4}$ is $1 \dfrac{7}{8}$?

Answer: $1 \dfrac{1}{2}$

Exercises

Exercise $\PageIndex{1}$

Find $\dfrac{2}{3}$ of $\dfrac{3}{4}$.

Answer: $\dfrac{1}{2}$

Exercise $\PageIndex{2}$

Find $\dfrac{5}{8}$ of $\dfrac{1}{10}$.

Exercise $\PageIndex{3}$

Find $\dfrac{12}{13}$ of $\dfrac{13}{36}$.

Answer: $\dfrac{1}{3}$

Exercise $\PageIndex{4}$

Find $\dfrac{1}{4}$ of $\dfrac{4}{7}$.

Exercise $\PageIndex{5}$

$\dfrac{3}{10}$ of $\dfrac{15}{4}$ is what number?

Answer: $\dfrac{9}{8}$ or $1 \dfrac{1}{8}$

Exercise $\PageIndex{6}$

$\dfrac{14}{15}$ of $\dfrac{20}{21}$ is what number?

Exercise $\PageIndex{7}$

$\dfrac{3}{44}$ of $\dfrac{11}{12}$ is what number?

Answer: $\dfrac{1}{16}$

Exercise $\PageIndex{8}$

$\dfrac{1}{3}$ of 2 is what number?

Exercise $\PageIndex{9}$

$\dfrac{1}{4}$ of 3 is what number?

Answer: $\dfrac{3}{4}$

Exercise $\PageIndex{10}$

$\dfrac{1}{10}$ of $\dfrac{1}{100}$ is what number?

Exercise $\PageIndex{11}$

$\dfrac{1}{100}$ of $\dfrac{1}{10}$ is what number?

Answer: $\dfrac{1}{1,000}$

Exercise $\PageIndex{12}$

$1 \dfrac{5}{9}$ of $2 \dfrac{4}{7}$ is what number?

Exercise $\PageIndex{13}$

$1 \dfrac{7}{18}$ of $\dfrac{4}{15}$ is what number?

Answer: $\dfrac{10}{27}$

Exercise $\PageIndex{14}$

$1 \dfrac{1}{8}$ of $1 \dfrac{11}{16}$ is what number?

Exercise $\PageIndex{15}$

Find $\dfrac{2}{3}$ of $\dfrac{1}{6}$ of $\dfrac{9}{2}$.

Answer: $\dfrac{1}{2}$

Exercise $\PageIndex{16}$

Find $\dfrac{5}{8}$ of $\dfrac{9}{20}$ of $\dfrac{4}{9}$.

Exercise $\PageIndex{17}$

$\dfrac{5}{12}$ of what number is $\dfrac{5}{6}$?

Answer: 2

Exercise $\PageIndex{18}$

$\dfrac{3}{14}$ of what number is $\dfrac{6}{7}$?

Exercise $\PageIndex{19}$

$\dfrac{10}{3}$ of what number is $\dfrac{5}{9}$?

Answer: $\dfrac{1}{6}$

Exercise $\PageIndex{20}$

$\dfrac{15}{7}$ of what number is $\dfrac{20}{21}$?

Exercise $\PageIndex{21}$

$\dfrac{8}{3}$ of what number is $1 \dfrac{7}{9}$?

Answer: $\dfrac{2}{3}$

Exercise $\PageIndex{22}$

$\dfrac{1}{3}$ of what number is $\dfrac{1}{3}$?

Exercise $\PageIndex{23}$

$\dfrac{1}{6}$ of what number is $\dfrac{1}{6}$?

Answer: 1

Exercise $\PageIndex{24}$

$\dfrac{3}{4}$ of what number is $\dfrac{3}{4}$?

Exercise $\PageIndex{25}$

$\dfrac{8}{11}$ of what number is $\dfrac{8}{11}$?

Answer: 1

Exercise $\PageIndex{26}$

$\dfrac{3}{8}$ of what number is 0?

Exercise $\PageIndex{27}$

$\dfrac{2}{3}$ of what number is 1?

Answer: $\dfrac{3}{2}$ or $1 \dfrac{1}{2}$

Exercise $\PageIndex{28}$

$3 \dfrac{1}{5}$ of what number is 1?

Exercise $\PageIndex{29}$

$1 \dfrac{9}{12}$ of what number is $5 \dfrac{1}{4}$?

Answer: 3

Exercise $\PageIndex{30}$

$3 \dfrac{1}{25}$ of what number is $2 \dfrac{8}{15}$?

Exercise $\PageIndex{31}$

What part of $\dfrac{2}{3}$ is $1 \dfrac{1}{9}$?

Answer: $\dfrac{5}{3}$ or $1 \dfrac{2}{3}$

Exercise $\PageIndex{32}$

What part of $\dfrac{9}{10}$ is $3 \dfrac{3}{5}$?

Exercise $\PageIndex{33}$

What part of $\dfrac{8}{9}$ is $\dfrac{3}{5}$?

Answer: $\dfrac{27}{40}$

Exercise $\PageIndex{34}$

What part of $\dfrac{14}{15}$ is $\dfrac{7}{30}$?

Exercise $\PageIndex{35}$

What part of 3 is $\dfrac{1}{5}$?

Answer: $\dfrac{1}{15}$

Exercise $\PageIndex{36}$

What part of 8 is $\dfrac{2}{3}$?

Exercise $\PageIndex{37}$

What part of 24 is 9?

Answer: $\dfrac{3}{8}$

Exercise $\PageIndex{38}$

What part of 42 is 26?

Exercise $\PageIndex{39}$

Find $\dfrac{12}{13}$ of $\dfrac{39}{40}$.

Answer: $\dfrac{9}{10}$

Exercise $\PageIndex{40}$

$\dfrac{14}{15}$ of $\dfrac{12}{21}$ is what number?

Exercise $\PageIndex{41}$

$\dfrac{8}{15}$ of what number is $2 \dfrac{2}{5}$?

Answer: $\dfrac{9}{2} = 4 \dfrac{1}{2}$

Exercise $\PageIndex{42}$

$\dfrac{11}{15}$ of what number is $\dfrac{22}{35}$?

Exercise $\PageIndex{43}$

$\dfrac{11}{16}$ of what number is 1?

Answer: $\dfrac{16}{11}$ or $1 \dfrac{5}{11}$

Exercise $\PageIndex{44}$

What part of $\dfrac{23}{40}$ is $3 \dfrac{9}{20}$?

Exercise $\PageIndex{45}$

$\dfrac{4}{35}$ of $3 \dfrac{9}{22}$ is what number?

Answer: $\dfrac{30}{77}$

Exercises for Review

Exercise $\PageIndex{46}$

Use the numbers 2 and 7 to illustrate the commutative property of addition.

Exercise $\PageIndex{47}$

Is 4 divisible by 0?

Answer: no

Exercise $\PageIndex{48}$

Expand $3^7$. Do not find the actual value.

Exercise $\PageIndex{49}$

Convert $3 \dfrac{5}{12}$ to an improper fraction.

Answer: $\dfrac{41}{12}$

Exercise $\PageIndex{50}$

Find the value of $\dfrac{3}{8}$ \div \dfrac{9}{16} \cdot \dfrac{6}{5}\).

Search

Text Color

Text Size

Margin Size

Font Type

Sample Set A