6.2: Converting a Decimal to a Fraction
- Page ID
- 48865
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- be able to convert an ordinary decimal and a complex decimal to a fraction
Converting an Ordinary Decimal to a Fraction
We can convert a decimal fraction to a fraction, essentially, by saying it in words, then writing what we say. We may have to reduce that fraction.
Convert each decimal fraction to a proper fraction or a mixed number.

Solution
Reading: six tenths \(\to \dfrac{6}{10}\).
Reduce: \(\dfrac{3}{5}\)
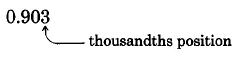
Solution
Reading: nine hundred three thousands \(\to \dfrac{903}{1000}\).

Solution
Reading: eighteen and sixty-one hundredths \(\to 18 \dfrac{61}{100}\).
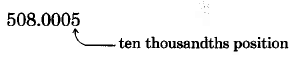
Solution
Reading: five hundred eight and five ten thousandths \(\to 508 \dfrac{5}{10,000}\).
Reduce: \(508 \dfrac{1}{2,000}\).
Practice Set A
Convert the following decimals to fractions or mixed numbers. Be sure to reduce.
16.84
- Answer
-
\(16 \dfrac{21}{25}\)
Practice Set A
0.513
- Answer
-
\(\dfrac{513}{1,000}\)
Practice Set A
6,646.0107
- Answer
-
\(6,646 \dfrac{107}{10,000}\)
Practice Set A
1.1
- Answer
-
\(1 \dfrac{1}{10}\)
Converting A Complex Decimal to a Fraction
Numbers such as \(0.11 \dfrac{2}{3}\) are called complex decimals. We can also convert complex decimals to fractions.
Convert the following complex decimals to fractions.
\(0.11 \dfrac{2}{3}\)
Solution
The \(\dfrac{2}{3}\) appears to occur in the thousands position, but it is referring to \(\dfrac{2}{3}\) of a hundredth. So, we read \(0.11 \dfrac{2}{3}\) as "eleven and two-thirds hundredths."
\(\begin{array} {rcl} {0.11 \dfrac{2}{3} = \dfrac{11 \dfrac{2}{3}}{100}} & = & {\dfrac{\dfrac{11 \cdot 3 + 2}{3}}{100}} \\ {} & = & {\dfrac{\dfrac{35}{3}}{\dfrac{100}{1}}} \\ {} & = & {\dfrac{35}{3} \div \dfrac{100}{1}} \\ {} & = & {\dfrac{\begin{array} {c} {^7} \\ {\cancel{35}} \end{array}}{3} \cdot \dfrac{1}{\begin{array} {c} {\cancel{100}} \\ {^{20}} \end{array}}} \\ {} & = & {\dfrac{7}{60}} \end{array}\)
\(4.006 \dfrac{1}{4}\)
Solution
Note that \(4.006 \dfrac{1}{4} = 4 + .006 \dfrac{1}{4}\)
\(\begin{array} {rcl} {4 + .006 \dfrac{1}{4}} & = & {4 + \dfrac{6 \dfrac{1}{4}}{1000}} \\ {} & = & {4 + \dfrac{\dfrac{25}{4}}{\dfrac{1000}{1}}} \\ {} & = & {4 + \dfrac{\begin{array} {c} {^1} \\ {\cancel{25}} \end{array}}{4} \cdot \dfrac{1}{\begin{array} {c} {\cancel{1000}} \\ {^{40}} \end{array}}} \\ {} & = & {4 + \dfrac{1 \cdot 1}{4 \cdot 40}} \\ {} & = & {4 + \dfrac{1}{160}} \\ {} & = & {4 \dfrac{1}{160}} \end{array}\)
Practice Set B
Convert each complex decimal to a fraction or mixed number. Be sure to reduce.
\(0.8 \dfrac{3}{4}\)
- Answer
-
\(\dfrac{7}{8}\)
Practice Set B
\(0.12 \dfrac{2}{5}\)
- Answer
-
\(\dfrac{31}{250}\)
Practice Set B
\(6.005 \dfrac{5}{6}\)
- Answer
-
\(6 \dfrac{7}{1,200}\)
Practice Set B
\(18.1 \dfrac{3}{17}\)
- Answer
-
\(18 \dfrac{2}{17}\)
Exercises
For the following 20 problems, convert each decimal fraction to a proper fraction or a mixed number. Be sure to reduce.
Exercise \(\PageIndex{1}\)
0.7
- Answer
-
\(\dfrac{7}{10}\)
Exercise \(\PageIndex{2}\)
0.1
Exercise \(\PageIndex{3}\)
0.53
- Answer
-
\(\dfrac{53}{100}\)
Exercise \(\PageIndex{4}\)
0.71
Exercise \(\PageIndex{5}\)
0.219
- Answer
-
\(\dfrac{219}{1,000}\)
Exercise \(\PageIndex{6}\)
0.811
Exercise \(\PageIndex{7}\)
4.8
- Answer
-
\(4 \dfrac{4}{5}\)
Exercise \(\PageIndex{8}\)
2.6
Exercise \(\PageIndex{9}\)
16.12
- Answer
-
\(16 \dfrac{3}{25}\)
Exercise \(\PageIndex{10}\)
25.88
Exercise \(\PageIndex{11}\)
6.0005
- Answer
-
\(6 \dfrac{1}{2,000}\)
Exercise \(\PageIndex{12}\)
1.355
Exercise \(\PageIndex{13}\)
16.125
- Answer
-
\(16 \dfrac{1}{8}\)
Exercise \(\PageIndex{14}\)
0.375
Exercise \(\PageIndex{15}\)
3.04
- Answer
-
\(3 \dfrac{1}{25}\)
Exercise \(\PageIndex{16}\)
21.1875
Exercise \(\PageIndex{17}\)
8.225
- Answer
-
\(8 \dfrac{9}{40}\)
Exercise \(\PageIndex{18}\)
1.0055
Exercise \(\PageIndex{19}\)
9.99995
- Answer
-
\(9 \dfrac{19,999}{20,000}\)
Exercise \(\PageIndex{20}\)
22.110
For the following 10 problems, convert each complex decimal to a fraction.
Exercise \(\PageIndex{21}\)
\(0.7 \dfrac{1}{2}\)
- Answer
-
\(\dfrac{3}{4}\)
Exercise \(\PageIndex{22}\)
\(0.012 \dfrac{1}{2}\)
Exercise \(\PageIndex{23}\)
\(2.16 \dfrac{1}{4}\)
- Answer
-
\(2 \dfrac{13}{80}\)
Exercise \(\PageIndex{24}\)
\(5.18 \dfrac{2}{3}\)
Exercise \(\PageIndex{25}\)
\(14.112 \dfrac{1}{3}\)
- Answer
-
\(14 \dfrac{337}{3,000}\)
Exercise \(\PageIndex{26}\)
\(80.0011 \dfrac{3}{7}\)
Exercise \(\PageIndex{27}\)
\(1.40 \dfrac{5}{16}\)
- Answer
-
\(1 \dfrac{129}{320}\)
Exercise \(\PageIndex{28}\)
\(0.8 \dfrac{5}{3}\)
Exercise \(\PageIndex{29}\)
\(1.9 \dfrac{7}{5}\)
- Answer
-
\(2 \dfrac{1}{25}\)
Exercise \(\PageIndex{30}\)
\(1.7 \dfrac{37}{9}\)
Exercises for Review
Exercise \(\PageIndex{31}\)
Find the greatest common factor of 70, 182, and 154.
- Answer
-
14
Exercise \(\PageIndex{32}\)
Find the greatest common multiple of 14, 26, and 60.
Exercise \(\PageIndex{33}\)
Find the value of \(\dfrac{3}{5} \cdot \dfrac{15}{18} \div \dfrac{5}{9}\).
- Answer
-
\(\dfrac{9}{10}\)
Exercise \(\PageIndex{34}\)
Find the value of \(5 \dfrac{2}{3} + 8 \dfrac{1}{12}\).
Exercise \(\PageIndex{35}\)
In the decimal number 26.10742, the digit 7 is in what position?
- Answer
-
thousandths


