6.3: Rounding Decimals
- Page ID
- 48866
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- be able to round a decimal number to a specified position
Rounding Decimal Numbers
We first considered the concept of rounding numbers in [link] where our concern with rounding was related to whole numbers only. With a few minor changes, we can apply the same rules of rounding to decimals.
To round a decimal to a particular position:
- Mark the position of the round-off digit (with an arrow or check).
- Note whether the digit to the immediate right of the marked digit is
- less than 5. If so, leave the round-off digit unchanged.
- 5 or greater. If so, add 1 to the round-off digit.
- If the round-off digit is
- to the right of the decimal point, eliminate all the digits to its right.
- to the left of the decimal point, replace all the digits between it and the decimal point with zeros and eliminate the decimal point and all the decimal digits.
Round each decimal to the specified position. (The numbers in parentheses indicate which step is being used.)
Round 32.116 to the nearest hundredth.
Solution
1: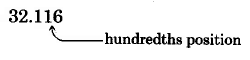 
2b: The digit immediately to the right is 6, and \(6 > 5\), so we add 1 to the round-off digit:
\(1 + 1 = 2\)
3a: The round-off digit is to the right of the decimal point, so we eliminate all digits to its right.
32.12
The number 32.116 rounded to the nearest hundredth is 32.12.
Round 633.14216 to the nearest hundred.
Solution
1: 
2a: The digit immediately to the right is 3, and \(3 < 5\) so we leave the round-off digit unchanged.
3b: The round-off digit is to the left of 0, so we replace all the digits between it and the decimal point with zeros and eliminate the decimal point and all the decimal digits.
600
The number 633.14216 rounded to the nearest hundred is 600.
1,729.63 rounded to the nearest ten is 1,730.
1.0144 rounded to the nearest tenth is 1.0.
60.98 rounded to the nearest one is 61.
Sometimes we hear a phrase such as "round to three decimal places." This phrase means that the round-off digit is the third decimal digit (the digit in the thousandths position).
67.129 rounded to the second decimal place is 67.13.
67.129558 rounded to 3 decimal places is 67.130.
Practice Set A
Round each decimal to the specified position.
4.816 to the nearest hundredth.
- Answer
-
4.82
Practice Set A
0.35928 to the nearest ten thousandths.
- Answer
-
0.3593
Practice Set A
82.1 to the nearest one.
- Answer
-
82
Practice Set A
753.98 to the nearest hundred.
- Answer
-
800
Practice Set A
Round 43.99446 to three decimal places.
- Answer
-
43.994
Practice Set A
Round 105.019997 to four decimal places.
- Answer
-
105.0200
Practice Set A
Round 99.9999 to two decimal places.
- Answer
-
100.00
Exercises
For the first 10 problems, complete the chart by rounding each decimal to the indicated positions.
Exercise \(\PageIndex{1}\)
20.01071
| Tenth | Hundredth | Thousandth | Ten Thousandth |
- Answer
-
Tenth Hundredth Thousandth Ten Thousandth 20.0 20.01 20.011 20.0107
Exercise \(\PageIndex{2}\)
3.52612
| Tenth | Hundredth | Thousandth | Ten Thousandth |
| 3.53 |
Exercise \(\PageIndex{3}\)
531.21878
| Tenth | Hundredth | Thousandth | Ten Thousandth |
- Answer
-
Tenth Hundredth Thousandth Ten Thousandth 531.2 531.22 531.219 531.2188
Exercise \(\PageIndex{4}\)
36.109053
| Tenth | Hundredth | Thousandth | Ten Thousandth |
| 36.1 |
Exercise \(\PageIndex{5}\)
1.999994
| Tenth | Hundredth | Thousandth | Ten Thousandth |
- Answer
-
Tenth Hundredth Thousandth Ten Thousandth 2.0 2.00 2.000 2.0000
Exercise \(\PageIndex{6}\)
7.4141998
| Tenth | Hundredth | Thousandth | Ten Thousandth |
| 7.414 |
Exercise \(\PageIndex{7}\)
0.000007
| Tenth | Hundredth | Thousandth | Ten Thousandth |
- Answer
-
Tenth Hundredth Thousandth Ten Thousandth 0.0 0.00 0.000 0.0000
Exercise \(\PageIndex{8}\)
0.00008
| Tenth | Hundredth | Thousandth | Ten Thousandth |
| 0.0001 |
Exercise \(\PageIndex{9}\)
9.19191919
| Tenth | Hundredth | Thousandth | Ten Thousandth |
- Answer
-
Tenth Hundredth Thousandth Ten Thousandth 9.2 9.19 9.192 9.1919
Exercise \(\PageIndex{10}\)
0.0876543
| Tenth | Hundredth | Thousandth | Ten Thousandth |
Calculator Problems
For the following 5 problems, round 18.4168095 to the indicated place.
Exercise \(\PageIndex{11}\)
3 decimal places.
- Answer
-
18.417
Exercise \(\PageIndex{12}\)
1 decimal place.
Exercise \(\PageIndex{13}\)
5 decimal places.
- Answer
-
18.41681
Exercise \(\PageIndex{14}\)
6 decimal places.
Exercise \(\PageIndex{15}\)
2 decimal places.
- Answer
-
18.42
Calculator Problems
For the following problems, perform each division using a calculator.
Exercise \(\PageIndex{16}\)
\(4 \div 3\) and round to 2 decimal places.
Exercise \(\PageIndex{17}\)
\(1 \div 8\) and round to 1 decimal place.
- Answer
-
0.1
Exercise \(\PageIndex{18}\)
\(1 \div 27\) and round to 6 decimal places.
Exercise \(\PageIndex{19}\)
\(51 \div 61\) and round to 5 decimal places.
- Answer
-
0.83607
Exercise \(\PageIndex{20}\)
\(3 \div 16\) and round to 3 decimal places.
Exercise \(\PageIndex{21}\)
\(16 \div 3\) and round to 3 decimal places.
- Answer
-
5.333
Exercise \(\PageIndex{22}\)
\(26 \div 7\) and round to 5 decimal places.
Exercises for Review
Exercise \(\PageIndex{23}\)
What is the value of 2 in the number 421,916,017?
- Answer
-
Ten million
Exercise \(\PageIndex{24}\)
Perform the division: \(378 \div 29\).
Exercise \(\PageIndex{25}\)
Find the value of \(4^4\).
- Answer
-
256
Exercise \(\PageIndex{26}\)
Convert \(\dfrac{11}{3}\) to a mixed number.
Exercise \(\PageIndex{27}\)
Convert 3.16 to a mixed number fraction.
- Answer
-
\(3 \dfrac{4}{25}\)