6.6: Division of Decimals

Last updated
Save as PDF

Page ID: 48869

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

understand the method used for dividing decimals
be able to divide a decimal number by a nonzero whole number and by another, nonzero, decimal number
be able to simplify a division of a decimal by a power of 10

The Logic Behind the Method

As we have done with addition, subtraction, and multiplication of decimals, we will study a method of division of decimals by converting them to fractions, then we will make a general rule.

We will proceed by using this example: Divide 196.8 by 6.

$\begin{array} {r} {32\ \ \ } \\ {6\overline{)196.8}} \\ {\underline{18\ \ \ \ \ }} \\ {16\ \ \ } \\ {\underline{12\ \ \ }} \\ {4\ \ \ } \end{array}$

We have, up to this point, divided 196.8 by 6 and have gotten a quotient of 32 with a remainder of 4. If we follow our intuition and bring down the .8, we have the division $4.8 \div 6$.

$\begin{array} {rcl} {4.8 \div 6} & = & {4 \dfrac{8}{10} \div 6} \\ {} & = & {\dfrac{48}{10} \div \dfrac{6}{1}} \\ {} & = & {\dfrac{\begin{array} {c} {^8} \\ {\cancel{48}} \end{array}}{10} \cdot \dfrac{1}{\begin{array} {c} {\cancel{6}} \\ {^1} \end{array}}} \\ {} & = & {\dfrac{8}{10}} \end{array}$

Thus, $4.8 \div 6 = .8$.

Now, our intuition and experience with division direct us to place the .8 immediately to the right of 32.

$Long division. 196.8 divided by 6. 6 goes into 19 3 times, with a remainder of 1. Bring the 6 down. 6 goes into 16 twice, with a remainder of 4. Bring the 8 down, and the decimal place with it. 6 goes into 48 8 times, with a remainder of zero. The quotient is 32.8 Notice that the decimal points appear in the same column.$

From these observations, we suggest the following method of division.

A Method of Dividing a Decimal by a Nonzero Whole Number

Method of Dividing a Decimal by a Nonzero Whole Number
To divide a decimal by a nonzero whole number:

Write a decimal point above the division line and directly over the decimal point of the dividend.
Proceed to divide as if both numbers were whole numbers.
If, in the quotient, the first nonzero digit occurs to the right of the decimal point, but not in the tenths position, place a zero in each position between the decimal point and the first nonzero digit of the quotient.

Sample Set A

Find the decimal representations of the following quotients.

$114.1 \div 7 = 7$

Solution

$\begin{array} {r} {16.3} \\ {7 \overline{)114.1}} \\ {\underline{7\ \ \ \ \ }} \\ {44\ \ \ } \\ {\underline{42\ \ \ }} \\ {2.1} \\ {\underline{2.1}} \\ {0} \end{array}$

Thus, $114.1 \div 7 = 16.3$

Check: If $114.1 \div 7 = 16.3$, then $7 \cdot 16.3$ should equal 114.1.

$\begin{array} {r} {^{4.2\ \ \ }} \\ {16.3} \\ {\underline{\ \ \ \ \ \ \ 7}} \\ {114.1} \end{array}$ True.

Sample Set A

$0.02068 \div 4$

Solution

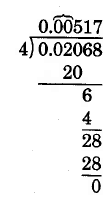
$Long division. 0.02068 divided by 4. 4 goes into 20 5 times, with no remainder. 4 goes into 6 once, with a remainder of 2. Bring down the 8. 4 goes into 28 7 times, with a remainder of zero. The quotient is 0.00517.$

Place zeros in the tenths and hundredths positions. (See Step 3.)

Thus, $0.02068 \div 4 = 0.00517$.

Practice Set A

Find the following quotients.

$184.5 \div 3$

Answer: 61.5

Practice Set A

$16.956 \div 9$

Answer: 1.884

Practice Set A

$0.2964 \div 4$

Answer: 0.0741

Practice Set A

$0.000496 \div 8$

Answer: 0.000062

A Method of Dividing a Decimal By a Nonzero Decimal

Now that we can divide decimals by nonzero whole numbers, we are in a position to divide decimals by a nonzero decimal. We will do so by converting a division by a decimal into a division by a whole number, a process with which we are already familiar. We'll illustrate the method using this example: Divide 4.32 by 1.8.

Let's look at this problem as $4 \dfrac{32}{100} \div 1 \dfrac{8}{10}$.

$\begin{array} {4 \dfrac{32}{100} \div 1 \dfrac{8}{10}} & = & {\dfrac{4 \dfrac{32}{100}}{1 \dfrac{8}{10}}} \\ {} & = & {\dfrac{\dfrac{432}{100}}{\dfrac{18}{10}}} \end{array}$

The divisor is $\dfrac{18}{10}$. We can convert $\dfrac{18}{10}$ into a whole number if we multiply it by 10.

$\dfrac{18}{10} \cdot 10 = \dfrac{18}{\begin{array} {c} {\cancel{10}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{10}} \end{array}}{1} = 18$

But, we know from our experience with fractions, that if we multiply the denominator of a fraction by a nonzero whole number, we must multiply the numerator by that same nonzero whole number. Thus, when converting $\dfrac{18}{10}$ to a whole number by multiplying it by 10, we must also multiply the numerator $\dfrac{432}{100}$ by 10.

$\begin{array} {rcl} {\dfrac{432}{100} \cdot 10 = \dfrac{432}{\begin{array} {c} {\cancel{100}} \\ {^{10}} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{10}} \end{array}}{1}} & = & {\dfrac{432 \cdot 1}{10 \cdot 1} = \dfrac{432}{10}} \\ {} & = & {43 \dfrac{2}{10}} \\ {} & = & {43.2} \end{array}$

We have converted the division $4.32 \div 1.8$ into the division $43.2 \div 18$, that's is,

$1.8\overline{)4.32} \to 18 \overline{)43.2}$

Notice what has occurred.

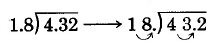
$4.32 divided by 1.8. The decimal place in both numbers is moved to the right by one space.$

If we "move" the decimal point of the divisor one digit to the right, we must also "move" the decimal point of the dividend one place to the right. The word "move" actually indicates the process of multiplication by a power of 10.

Method of Dividing a Decimal by a Decimal NumberTo divide a decimal by a nonzero decimal,

Convert the divisor to a whole number by moving the decimal point to the position immediately to the right of the divisor's last digit.
Move the decimal point of the dividend to the right the same number of digits it was moved in the divisor.
Set the decimal point in the quotient by placing a decimal point directly above the newly located decimal point in the dividend.
Divide as usual.

Sample Set B

Find the following quotients.

$32.66 \div 7.1$

Solution

$7.1 \underline{)32.66}$

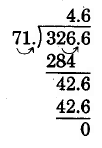
$Long division. 32.66 divided by 7.1. Move the decimal place to the right for both numbers, making 326.6 divided by 71. 71 goes into 326 4 times, with a remainder of 42. Bring down the 6. 71 goes into 426 6 times, with a remainder of zero. The quotient is 4.6$

The divisor has one decimal place.
Move the decimal point of both the divisor and the dividend 1 place to the right.
Set the decimal point.
Divide as usual.

Thus, $32.66 \div 7.1 = 4.6$

Check: $32.66 \div 7.1 = 4.6$ if $4.6 \times 7.1 = 32.66$

$\begin{array} {c} {4.6} \\ {\underline{\times 7.1}} \\ {46} \\ {\underline{322\ \ }} \\ {32.66} \end{array}$ True.

Sample Set B

$1.0773 \div 0.513$

Solution

$7.1 \underline{)32.66}$

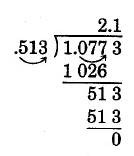
$Long division. 1.0773 divided by .513. Move the decimal place three spaces to the right. 513 goes into 1077 twice, with a remainder of 51. Bring down the 3. 513 goes into 513 exactly once. The quotient is 2.1.$

The divisor has 3 decimal places.
Move the decimal point of both the divisor and the dividend 3 places to the right.
Set the decimal place and divide.

Thus, $1.0773 \div 0.513 = 2.1$

Checking by multiplying 2.1 and 0.513 will convince us that we have obtained the correct result. (Try it.)

Sample Set B

$12 \div 0.00032$

Solution

$0.00032 \underline{)12.00000}$

The divisor has 5 decimal places.
Move the decimal point of both the divisor and the dividend 5 places to the right. We will need to add 5 zeros to 12.
Set the decimal place and divide.

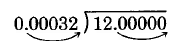
$12 divided by 0.00032. The decimal place needs to be moved five spaces to the right, which means that five zeros need to be added to the right of the 12 to perform the subtraction.$

his is now the same as the division of whole numbers.

$\begin{array} {r} {37500.} \\ {32 \overline{)1200000.}} \\ {\underline{96\ \ \ \ \ \ \ \ \ }} \\ {240\ \ \ \ \ \ \ } \\ {\underline{224\ \ \ \ \ \ \ }} \\ {160\ \ \ \ \ } \\ {\underline{160\ \ \ \ \ }} \\ {000} \end{array}$

Checking assures us that $12 \div 0.00032 = 37,500$.

Practice Set B

Find the decimal representation of each quotient.

$9.176 \div 3.1$

Answer: 2.96

Practice Set B

$5.0838 \div 1.11$

Answer: 4.58

Practice Set B

$16 \div 0.0004$

Answer: 40,000

Practice Set B

$8,162.41 \div 10$

Answer: 816.241

Practice Set B

$8,162.41 \div 100$

Answer: 81.6241

Practice Set B

$8,162.41 \div 1,000$

Answer: 8.16241

Practice Set B

$8,162.41 \div 10,000$

Answer: 0.816241

Calculators

Calculators can be useful for finding quotients of decimal numbers. As we have seen with the other calculator operations, we can sometimes expect only approximate results. We are alerted to approximate results when the calculator display is filled with digits. We know it is possible that the operation may produce more digits than the calculator has the ability to show. For example, the multiplication

$\underbrace{0.12345}_{\text{5 decimal places}} \times \underbrace{0.4567}_{\text{4 decimal places}}$

produces $5 + 4 = 9$ decimal places. An eight-digit display calculator only has the ability to show eight digits, and an approximation results. The way to recognize a possible approximation is illustrated in problem 3 of the next sample set.

Sample Set C

Find each quotient using a calculator. If the result is an approximation, round to five decimal places.

$12.596 \div 4.7$

Solution

		Display Reads
Type	12.596	12.596
Press	$\div$	12.596
Type	4.7	4.7
Press	=	2.68

Since the display is not filled, we expect this to be an accurate result.

Sample Set C

$0.5696376 \div 0.00123$

Solution

		Display Reads
Type	.5696376	0.5696376
Press	$\div$	0.5696376
Type	.00123	0.00123
Press	=	463.12

Since the display is not filled, we expect this result to be accurate.

Sample Set C

$0.8215199 \div 4.113$

Solution

		Display Reads
Type	.8215199	0.8215199
Press	$\div$	0.8215199
Type	4.113	4.113
Press	=	0.1997373

There are EIGHT DIGITS — DISPLAY FILLED! BE AWARE OF POSSIBLE APPROXIMATIONS.

We can check for a possible approximation in the following way. Since the division $\begin{array} {r} {3\ \ \ } \\ {4 \overline{)12}} \end{array}$ can be checked by multiplying 4 and 3, we can check our division by performing the multiplication

$\underbrace{4.113}_{\text{3 decimal places}} \times \underbrace{0.1997373}_{\text{7 decimal places}}$

This multiplication produces $3 + 7 = 10$ decimal digits. But our suspected quotient contains only 8 decimal digits. We conclude that the answer is an approximation. Then, rounding to five decimal places, we get 0.19974.

Practice Set C

Find each quotient using a calculator. If the result is an approximation, round to four decimal places.

$42.49778 \div 14.261$

Answer: 2.98

Practice Set C

$0.001455 \div 0.291$

Answer: 0.005

Practice Set C

$7.459085 \div 2.1192$

Answer: 3.5197645 is an approximate result. Rounding to four decimal places, we get 3.5198

Dividing Decimals By Powers of 10

In problems 4 and 5 of Practice Set B, we found the decimal representations of $8,162.41 \div 10$ and $8,162.41 \div 100$. Let's look at each of these again and then, from these observations, make a general statement regarding division of a decimal number by a power of 10.

$\begin{array} {r} {816.241} \\ {10 \overline{)8162.410}} \\ {\underline{80\ \ \ \ \ \ \ \ \ \ \ }} \\ {16\ \ \ \ \ \ \ \ \ } \\ {\underline{10\ \ \ \ \ \ \ \ \ }} \\ {62 \ \ \ \ \ \ \ } \\ {\underline{60\ \ \ \ \ \ \ }} \\ {24\ \ \ \ \ } \\ {\underline{20\ \ \ \ \ }} \\ {41\ \ \ } \\ {\underline{40\ \ \ }} \\ {10\ } \\ {\underline{10\ }} \\ {0\ } \end{array}$

Thus, $8,162.41 \div 10 = 816.241$

Notice that the divisor 10 is composed of one 0 and that the quotient 816.241 can be obtained from the dividend 8,162.41 by moving the decimal point one place to the left.

$\begin{array} {r} {81.6241} \\ {100 \overline{)8162.4100}} \\ {\underline{800\ \ \ \ \ \ \ \ \ \ \ }} \\ {162\ \ \ \ \ \ \ \ \ } \\ {\underline{100\ \ \ \ \ \ \ \ \ }} \\ {624 \ \ \ \ \ \ \ } \\ {\underline{600\ \ \ \ \ \ \ }} \\ {241\ \ \ \ \ } \\ {\underline{200\ \ \ \ \ }} \\ {410\ \ \ } \\ {\underline{400\ \ \ }} \\ {100\ } \\ {\underline{100\ }} \\ {0\ } \end{array}$

Thus, $8,162.41 \div 100 = 81.6241$.

Notice that the divisor 100 is composed of two 0's and that the quotient 81.6241 can be obtained from the dividend by moving the decimal point two places to the left.

Using these observations, we can suggest the following method for dividing decimal numbers by powers of 10.

Dividing a Decimal Fraction by a Power of 10
To divide a decimal fraction by a power of 10, move the decimal point of the decimal fraction to the left as many places as there are zeros in the power of 10. Add zeros if necessary.

Sample Set D

Find each quotient.

$9,248.6 \div 100$

Solution

Since there are 2 zeros in this power of 10, we move the decimal point 2 places to the left.

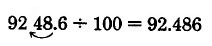
$9248.6 divided by 100 is equal to 92.480. Notice that the only effect is the movement of a decimal two places to the left of 9248.6.$

Sample Set D

$3.28 \div 10,000$

Solution

Since there are 4 zeros in this power of 10, we move the decimal point 4 places to the left. To do so, we need to add three zeros.

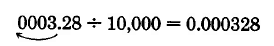
$3.28 divided by 10,000 is equal to 0.000328. Notice that the only effect is the movement of a decimal four places to the left of 0003.28.$

Practice Set D

Find the decimal representation of each quotient.

$182.5 \div 10$

Answer: 18.25

Practice Set D

$182.5 \div 100$

Answer: 1.825

Practice Set D

$182.5 \div 1,000$

Answer: 0.1825

Practice Set D

$182.5 \div 10,000$

Answer: 0.01825

Practice Set D

$646.18 \div 100$

Answer: 6.4618

Practice Set D

$21.926 \div 1,000$

Answer: 0.021926

Exercises

For the following 30 problems, find the decimal representation of each quotient. Use a calculator to check each result.

Exercise $\PageIndex{1}$

$4.8 \div 3$

Answer: 1.6

Exercise $\PageIndex{2}$

$16.8 \div 8$

Exercise $\PageIndex{3}$

$18.5 \div 5$

Answer: 3.7

Exercise $\PageIndex{4}$

$12.33 \div 3$

Exercise $\PageIndex{5}$

$54.36 \div 9$

Answer: 6.04

Exercise $\PageIndex{6}$

$73.56 \div 12$

Exercise $\PageIndex{7}$

$159.46 \div 17$

Answer: 9.38

Exercise $\PageIndex{8}$

$12.16 \div 64$

Exercise $\PageIndex{9}$

$37.26 \div 81$

Answer: 0.46

Exercise $\PageIndex{10}$

$439.35 \div 435$

Exercise $\PageIndex{11}$

$36.98 \div 4.3$

Answer: 8.6

Exercise $\PageIndex{12}$

$46.41 \div 9.1$

Exercise $\PageIndex{13}$

$3.6 \div 1.5$

Answer: 2.4

Exercise $\PageIndex{14}$

$0.68 \div 1.7$

Exercise $\PageIndex{15}$

$60.301 \div 8.1$

Answer: 6.21

Exercise $\PageIndex{16}$

$2.832 \div 0.4$

Exercise $\PageIndex{17}$

$4.7524 \div 2.18$

Answer: 2.18

Exercise $\PageIndex{18}$

$16.2409 \div 4.03$

Exercise $\PageIndex{19}$

$1.002001 \div 1.001$

Answer: 1.001

Exercise $\PageIndex{20}$

$25.050025 \div 5.005$

Exercise $\PageIndex{21}$

$12.4 \div 3.1$

Answer: 4

Exercise $\PageIndex{22}$

$0.48 \div 0.08$

Exercise $\PageIndex{23}$

$30.24 \div 2.16$

Answer: 14

Exercise $\PageIndex{24}$

$48.87 \div 0.87$

Exercise $\PageIndex{25}$

$12.321 \div 0.111$

Answer: 111

Exercise $\PageIndex{26}$

$64,351.006 \div 10$

Exercise $\PageIndex{27}$

$64,351.006 \div 100$

Answer: 643.51006

Exercise $\PageIndex{28}$

$64,351.006 \div 1,000$

Exercise $\PageIndex{29}$

$64,351.006 \div 1,000,000$

Answer: 0.064351006

Exercise $\PageIndex{30}$

$0.43 \div 100$

For the following 5 problems, find each quotient. Round to the specified position. A calculator may be used.

Exercise $\PageIndex{31}$

$11.2944 \div 6.24$

Actual Quotient	Tenths	Hundredths	Thousandths

Answer

Actual Quotient	Tenths	Hundreds	Thousandths
1.81	1.8	1.81	1.810

Exercise $\PageIndex{32}$

$45.32931 \div 9.01$

Actual Quotient	Tenths	Hundredths	Thousandths

Exercise $\PageIndex{33}$

$3.18186 \div 0.66$

Actual Quotient	Tenths	Hundredths	Thousandths

Answer

Actual Quotient	Tenths	Hundreds	Thousandths
4.821	4.8	4.82	4.821

Exercise $\PageIndex{34}$

$4.3636 \div 4$

Actual Quotient	Tenths	Hundredths	Thousandths

Exercise $\PageIndex{35}$

$0.00006318 \div 0.018$

Actual Quotient	Tenths	Hundredths	Thousandths

Answer

Actual Quotient	Tenths	Hundreds	Thousandths
0.00351	0.0	0.00	0.004

For the following 9 problems, find each solution.

Exercise $\PageIndex{36}$

Divide the product of 7.4 and 4.1 by 2.6.

Exercise $\PageIndex{37}$

Divide the product of 11.01 and 0.003 by 2.56 and round to two decimal places.

Answer: 0.01

Exercise $\PageIndex{38}$

Divide the difference of the products of 2.1 and 9.3, and 4.6 and 0.8 by 0.07 and round to one decimal place.

Exercise $\PageIndex{1}$

A ring costing $567.08 is to be paid off in equal monthly payments of $46.84. In how many months will the ring be paid off?

Answer: 12.11 months

Exercise $\PageIndex{39}$

Six cans of cola cost $2.58. What is the price of one can?

Exercise $\PageIndex{1}$

A family traveled 538.56 miles in their car in one day on their vacation. If their car used 19.8 gallons of gas, how many miles per gallon did it get?

Answer: 27.2 miles per gallon

Exercise $\PageIndex{40}$

Three college students decide to rent an apartment together. The rent is $812.50 per month. How much must each person contribute toward the rent?

Exercise $\PageIndex{41}$

A woman notices that on slow speed her video cassette recorder runs through 296.80 tape units in 10 minutes and at fast speed through 1098.16 tape units. How many times faster is fast speed than slow speed?

Answer: 3.7

Exercise $\PageIndex{42}$

A class of 34 first semester business law students pay a total of $1,354.90, disregarding sales tax, for their law textbooks. What is the cost of each book?

Calculator Problems
For the following problems, use calculator to find the quotients. If the result is approximate (see Sample Set C) round the result to three decimal places.

Exercise $\PageIndex{43}$

$3.8994 \div 2.01$

Answer: 1.94

Exercise $\PageIndex{44}$

$0.067444 \div 0.052$

Exercise $\PageIndex{45}$

$14,115.628 \div 484.74$

Answer: 29.120

Exercise $\PageIndex{46}$

$219,709.36 \div 9941.6$

Exercise $\PageIndex{47}$

$0.0852092 \div 0.49271$

Answer: 0.173

Exercise $\PageIndex{48}$

$2.4858225 \div 1.11611$

Exercise $\PageIndex{49}$

$0.123432 \div 0.1111$

Answer: 1.111

Exercise $\PageIndex{50}$

$2.102838 \div 1.0305$

Exercises for Review

Exercise $\PageIndex{51}$

Convert $4 \dfrac{7}{8}$ to an improper fraction.

Answer: $\dfrac{39}{8}$

Exercise $\PageIndex{52}$

$\dfrac{2}{7}$ of what number is $\dfrac{4}{5}$?

Exercise $\PageIndex{53}$

Find the sum. $\dfrac{4}{15} + \dfrac{7}{10} + \dfrac{3}{5}$.

Answer: $\dfrac{47}{30}$ or $1 \dfrac{17}{30}$

Exercise $\PageIndex{54}$

Round 0.01628 to the nearest ten-thousandths.

Exercise $\PageIndex{55}$

Find the product (2.06)(1.39)

Answer: 2.8634

Search

Text Color

Text Size

Margin Size

Font Type

Sample Set A

Sample Set A

Sample Set B

Sample Set B

Sample Set B

Sample Set C

Sample Set C

Sample Set C

Sample Set D

Sample Set D