6.5: Multiplication of Decimals
- Page ID
- 48868
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- understand the method used for multiplying decimals
- be able to multiply decimals
- be able to simplify a multiplication of a decimal by a power of 10
- understand how to use the word "of" in multiplication
The Logic Behind the Method
Consider the product of 3.2 and 1.46. Changing each decimal to a fraction, we have
\(\begin{array} {rcl} {(3.2)(1.46)} & = & {3 \dfrac{2}{10} \cdot 1 \dfrac{46}{100}} \\ {} & = & {\dfrac{32}{10} \cdot \dfrac{146}{100}} \\ {} & = & {\dfrac{32 \cdot 146}{10 \cdot 100}} \\ {} & = & {\dfrac{4672}{1000}} \\ {} & = & {4 \dfrac{672}{1000}} \\ {} & = & {\text{four and six hundred seventy-two thousandths}} \\ {} & = & {4.672} \end{array}\)
Thus, \((3.2)(1.46) = 4.672\)
Notice that the factor
\(\left \{ \begin{array} {c} {\text{3.2 has 1 decimal place,}} \\ {\text{1.46 has 2 decimal places,}} \\ {\text{and the product}} \\ {\text{4.672 has 3 decimal places.}} \end{array} \right \} 1 + 2 = 3\)
Using this observation, we can suggest that the sum of the number of decimal places in the factors equals the number of decimal places in the product.

The Method of Multiplying Decimals
To multiply decimals:
- Multiply the numbers as if they were whole numbers.
- Find the sum of the number of decimal places in the factors.
- The number of decimal places in the product is the sum found in step 2.
Find the following products.
\(6.5 \cdot 4.3\)
Solution
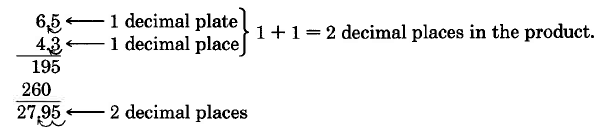
Thus, \(6.5 \cdot 4.3 = 27.95.\)
\(23.4 \cdot 1.96\)
Solution
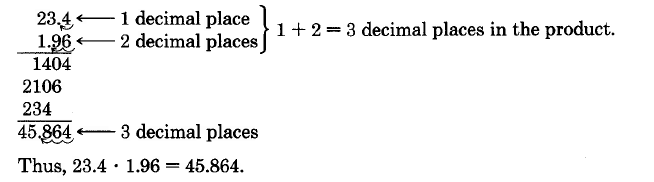
Thus, \(23.4 \cdot 1.96 = 45.864.\)
Find the product of 0.251 and 0.00113 and round to three decimal places.
Solution

Now, rounding to three decimal places, we get
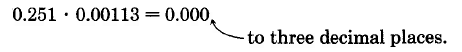
Practice Set A
Find the following products.
\(5.3 \cdot 8.6\)
- Answer
-
45.58
Practice Set A
\(2.12 \cdot 4.9\)
- Answer
-
10.388
Practice Set A
\(1.054 \cdot 0.16\)
- Answer
-
0.16864
Practice Set A
\(0.00031 \cdot 0.002\)
- Answer
-
0.00000062
Practice Set A
Find the product of 2.33 and 4.01 and round to one decimal place.
- Answer
-
9.3
Practice Set A
\(10 \cdot 5.394\)
- Answer
-
53.94
Practice Set A
\(100 \cdot 5.394\)
- Answer
-
539.4
Practice Set A
\(1000 \cdot 5.394\)
- Answer
-
5,394
Practice Set A
\(10,000 \cdot 5.394\)
- Answer
-
59,340
Calculators
Calculators can be used to find products of decimal numbers. However, a calculator that has only an eight-digit display may not be able to handle numbers or products that result in more than eight digits. But there are plenty of inexpensive ($50 - $75) calculators with more than eight-digit displays.
Find the following products, if possible, using a calculator.
\(2.58 \cdot 8.61\)
Solution
| Display Reads | ||
| Type | 2.58 | 2.58 |
| Press | \(\times\) | 2.58 |
| Type | 8.61 | 8.61 |
| Press | = | 22.2138 |
The product is 22.2138.
\(0.006 \cdot 0.0042\)
Solution
| Display Reads | ||
| Type | .006 | .006 |
| Press | \(\times\) | .006 |
| Type | .0042 | 0.0042 |
| Press | = | 0.0000252 |
We know that there will be seven decimal places in the product (since \(3 + 4 = 7\)). Since the display shows 7 decimal places, we can assume the product is correct. Thus, the product is 0.0000252.
\(0.0026 \cdot 0.11976\)
Solution
Since we expect \(4 + 5 = 9\) decimal places in the product, we know that an eight-digit display calculator will not be able to provide us with the exact value. To obtain the exact value, we must use "hand technology." Suppose, however, that we agree to round off this product to three decimal places. We then need only four decimal places on the display.
| Display Reads | ||
| Type | .0026 | .0026 |
| Press | \(\times\) | .0026 |
| Type | .11976 | 0.11976 |
| Press | = | 0.0003114 |
Rounding 0.0003114 to three decimal places we get 0.000. Thus, \(0.0026 \cdot 0.11976 = 0.000\) to three decimal places.
Practice Set B
Use a calculator to find each product. If the calculator will not provide the exact product, round the result to four decimal places.
\(5.126 \cdot 4.08\)
- Answer
-
20.91408
Practice Set B
\(0.00165 \cdot 0.04\)
- Answer
-
0.000066
Practice Set B
\(0.5598 \cdot 0.4281\)
- Answer
-
0.2397
Practice Set B
\(0.000002 \cdot 0.06\)
- Answer
-
0.0000
Multiplying Decimals by Powers of 10
There is an interesting feature of multiplying decimals by powers of 10. Consider the following multiplications.
| Multiplication | Number of Zeros in the Power of 10 | Number of Positions the Decimal Point Has Been Moved to the Right |
|---|---|---|
| \(10 \cdot 8.315274 = 83.15274\) | 1 | 1 |
| \(100 \cdot 8.315274 = 831.5274\) | 2 | 2 |
| \(1,000 \cdot 8.315274 = 8,315.274\) | 3 | 3 |
| \(10,000 \cdot 8.315274 = 83,152.74\) | 4 | 4 |
Multiplying a Decimal by a Power of 10
To multiply a decimal by a power of 10, move the decimal place to the right of its current position as many places as there are zeros in the power of 10. Add zeros if necessary.
Find the following products.
\(100 \cdot 34.876\). Since there are 2 zeros in 100, Move the decimal point in 34.876 two places to the right.
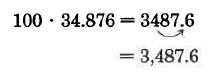
\(1,000 \cdot 4.8058\). Since there are 3 zeros in 1,000, move the decimal point in 4.8058 three places to the right.
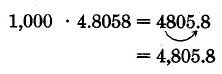
\(10,000 \cdot 56.82\). Since there are 4 zeros in 10,000, move the decimal point in 56.82 four places to the right. We will have to add two zeros in order to obtain the four places.
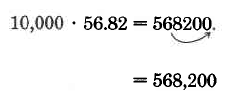
Since there is no fractional part, we can drop the decimal point.
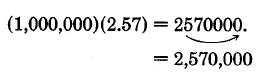

Practice Set C
Find the following products.
\(100 \cdot 4.27\).
- Answer
-
427
Practice Set C
\(10,000 \cdot 16.52187\).
- Answer
-
165,218.7
Practice Set C
\((10)(0.0188)\).
- Answer
-
0.188
Practice Set C
\((10,000,000,000)(52.7)\).
- Answer
-
527,000,000,000
Multiplication in Terms of “Of”
Recalling that the word "of" translates to the arithmetic operation of multiplication, let's observe the following multiplications.
Find 4.1 of 3.8.
Solution
Translating "of" to "\(\times\)", we get
\(\begin{array} {r} {4.1} \\ {\underline{\times 3.8}} \\ {328} \\ {\underline{123\ \ }} \\ {15.58} \end{array}\)
Find 0.95 of the sum of 2.6 and 0.8.
Solution
We first find the sum of 2.6 and 0.8.
\(\begin{array} {r} {2.6} \\ {\underline{+0.8}} \\ {3.4} \end{array}\)
Now find 0.95 of 3.4
\(\begin{array} {r} {3.4} \\ {\underline{\times 0.95}} \\ {170} \\ {\underline{306\ \ }} \\ {3.230} \end{array}\)
Thus, 0.95 of \((2.6 + 0.8)\) is 3.230.
Practice Set D
Find 2.8 of 6.4.
- Answer
-
17.92
Practice Set D
Find 0.1 of 1.3.
- Answer
-
0.13
Practice Set D
Find 1.01 of 3.6.
- Answer
-
3.636
Practice Set D
Find 0.004 of 0.0009.
- Answer
-
0.0000036
Practice Set D
Find 0.83 of 12.
- Answer
-
9.96
Practice Set D
Find 1.1 of the sum of 8.6 and 4.2.
- Answer
-
14.08
Exercises
For the following 30 problems, find each product and check each result with a calculator.
Exercise \(\PageIndex{1}\)
\(3.4 \cdot 9.2\)
- Answer
-
31.28
Exercise \(\PageIndex{2}\)
\(4.5 \cdot 6.1\)
Exercise \(\PageIndex{3}\)
\(8.0 \cdot 5.9\)
- Answer
-
47.20
Exercise \(\PageIndex{4}\)
\(6.1 \cdot 7\)
Exercise \(\PageIndex{5}\)
\((0.1)(1.52)\)
- Answer
-
0.152
Exercise \(\PageIndex{6}\)
\((1.99)(0.05)\)
Exercise \(\PageIndex{7}\)
\((12.52)(0.37)\)
- Answer
-
4.6324
Exercise \(\PageIndex{8}\)
\((5.116)(1.21)\)
Exercise \(\PageIndex{9}\)
\((31.82)(0.1)\)
- Answer
-
3.182
Exercise \(\PageIndex{10}\)
\((16.527)(9.16)\)
Exercise \(\PageIndex{11}\)
\(0.0021 \cdot 0.013\)
- Answer
-
0.0000273
Exercise \(\PageIndex{12}\)
\(1.0037 \cdot 1.00037\)
Exercise \(\PageIndex{13}\)
\((1.6)(1.6)\)
- Answer
-
2.56
Exercise \(\PageIndex{14}\)
\((4.2)(4.2)\)
Exercise \(\PageIndex{15}\)
\(0.9 \cdot 0.9\)
- Answer
-
0.81
Exercise \(\PageIndex{16}\)
\(1.11 \cdot 1.11\)
Exercise \(\PageIndex{17}\)
\(6.815 \cdot 4.3\)
- Answer
-
29.3045
Exercise \(\PageIndex{18}\)
\(9.0168 \cdot 1.2\)
Exercise \(\PageIndex{19}\)
\((3.5162)(0.0000003)\)
- Answer
-
0.00000105486
Exercise \(\PageIndex{20}\)
\((0.000001)(0.01)\)
Exercise \(\PageIndex{21}\)
\((10)(4.96)\)
- Answer
-
49.6
Exercise \(\PageIndex{22}\)
\((10)(36.17)\)
Exercise \(\PageIndex{23}\)
\(10 \cdot 421.8842\)
- Answer
-
4,218.842
Exercise \(\PageIndex{24}\)
\(10 \cdot 8.0107\)
Exercise \(\PageIndex{25}\)
\(100 \cdot 0.19621\)
- Answer
-
19.621
Exercise \(\PageIndex{26}\)
\(100 \cdot 0.779\)
Exercise \(\PageIndex{27}\)
\(1000 \cdot 3.596168\)
- Answer
-
3,596.168
Exercise \(\PageIndex{28}\)
\(1000 \cdot 42.7125571\)
Exercise \(\PageIndex{29}\)
\(1000 \cdot 25.01\)
- Answer
-
25,010
Exercise \(\PageIndex{30}\)
\(100,000 \cdot 9.923\)
Exercise \(\PageIndex{31}\)
\((4.6)(6.17)\)
| Actual product | Tenths | Hundreds | Thousandths |
- Answer
-
Actual product Tenths Hundreds Thousandths 28.382 28.4 28.38 28.382
Exercise \(\PageIndex{32}\)
\((8.09)(7.1)\)
| Actual product | Tenths | Hundreds | Thousandths |
Exercise \(\PageIndex{33}\)
\((11.1106)(12.08)\)
| Actual product | Tenths | Hundreds | Thousandths |
- Answer
-
Actual product Tenths Hundreds Thousandths 134.216048 134.2 134.22 134.216
Exercise \(\PageIndex{34}\)
\(0.0083 \cdot 1.090901\)
| Actual product | Tenths | Hundreds | Thousandths |
Exercise \(\PageIndex{35}\)
\(7 \cdot 26.518\)
| Actual product | Tenths | Hundreds | Thousandths |
- Answer
-
Actual product Tenths Hundreds Thousandths 185.626 185.6 185.63 185.626
For the following 15 problems, perform the indicated operations
Exercise \(\PageIndex{36}\)
Find 5.2 of 3.7.
Exercise \(\PageIndex{37}\)
Find 12.03 of 10.1
- Answer
-
121.503
Exercise \(\PageIndex{38}\)
Find 16 of 1.04
Exercise \(\PageIndex{39}\)
Find 12 of 0.1
- Answer
-
1.2
Exercise \(\PageIndex{40}\)
Find 0.09 of 0.003
Exercise \(\PageIndex{41}\)
Find 1.02 of 0.9801
- Answer
-
0.999702
Exercise \(\PageIndex{42}\)
Find 0.01 of the sum of 3.6 and 12.18
Exercise \(\PageIndex{43}\)
Find 0.2 of the sum of 0.194 and 1.07
- Answer
-
0.2528
Exercise \(\PageIndex{44}\)
Find the difference of 6.1 of 2.7 and 2.7 of 4.03
Exercise \(\PageIndex{45}\)
Find the difference of 0.071 of 42 and 0.003 of 9.2
- Answer
-
2.9544
Exercise \(\PageIndex{46}\)
If a person earns $8.55 an hour, how much does he earn in twenty-five hundredths of an hour?
Exercise \(\PageIndex{47}\)
A man buys 14 items at $1.16 each. What is the total cost?
- Answer
-
$16.24
Exercise \(\PageIndex{48}\)
In the problem above, how much is the total cost if 0.065 sales tax is added?
Exercise \(\PageIndex{49}\)
A river rafting trip is supposed to last for 10 days and each day 6 miles is to be rafted. On the third day a person falls out of the raft after only \(\dfrac{2}{5}\) of that day’s mileage. If this person gets discouraged and quits, what fraction of the entire trip did he complete?
- Answer
-
0.24
Exercise \(\PageIndex{50}\)
A woman starts the day with $42.28. She buys one item for $8.95 and another for $6.68. She then buys another item for sixty two-hundredths of the remaining amount. How much money does she have left?
Calculator Problems
For the following 10 problems, use a calculator to determine each product. If the calculator will not provide the exact product, round the results to five decimal places.
Exercise \(\PageIndex{51}\)
\(0.019 \cdot 0.321\)
- Answer
-
0.006099
Exercise \(\PageIndex{52}\)
\(0.261 \cdot 1.96\)
Exercise \(\PageIndex{53}\)
\(4.826 \cdot 4.827\)
- Answer
-
23.295102
Exercise \(\PageIndex{54}\)
\((9.46)^2\)
Exercise \(\PageIndex{55}\)
\((0.012)^2\)
- Answer
-
0.000144
Exercise \(\PageIndex{56}\)
\(0.00037 \cdot 0.0065\)
Exercise \(\PageIndex{57}\)
\(0.002 \cdot 0.0009\)
- Answer
-
0.0000018
Exercise \(\PageIndex{58}\)
\(0.1286 \cdot 0.7699\)
Exercise \(\PageIndex{59}\)
\(0.01 \cdot 0.00000471\)
- Answer
-
0.0000000471
Exercise \(\PageIndex{60}\)
\(0.00198709 \cdot 0.03\)
Exercises for Review
Exercise \(\PageIndex{61}\)
Find the value, if it exists, of \(0 \div 15\).
- Answer
-
0
Exercise \(\PageIndex{62}\)
Find the greatest common factor of 210, 231, and 357.
Exercise \(\PageIndex{63}\)
Reduce \(\dfrac{280}{2,156}\) to lowest terms.
- Answer
-
\(\dfrac{10}{77}\)
Exercise \(\PageIndex{64}\)
Write "fourteen and one hundred twenty-one ten-thousandths, using digits."
Exercise \(\PageIndex{65}\)
Subtract 6.882 from 8.661 and round the result to two decimal places.
- Answer
-
1.78


