9.5: Multiplicación de decimales

Last updated
Save as PDF

Page ID: 127642

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

entender el método utilizado para multiplicar decimales
poder multiplicar decimales
ser capaz de simplificar una multiplicación de un decimal por una potencia de 10
entender cómo usar la palabra “de” en la multiplicación

La lógica detrás del método

Considera el producto de 3.2 y 1.46. Cambiando cada decimal a una fracción, tenemos

$\begin{array} {rcl} {(3.2)(1.46)} & = & {3 \dfrac{2}{10} \cdot 1 \dfrac{46}{100}} \\ {} & = & {\dfrac{32}{10} \cdot \dfrac{146}{100}} \\ {} & = & {\dfrac{32 \cdot 146}{10 \cdot 100}} \\ {} & = & {\dfrac{4672}{1000}} \\ {} & = & {4 \dfrac{672}{1000}} \\ {} & = & {\text{four and six hundred seventy-two thousandths}} \\ {} & = & {4.672} \end{array}$

Por lo tanto,$(3.2)(1.46) = 4.672$

Observe que el factor

$\left \{ \begin{array} {c} {\text{3.2 has 1 decimal place,}} \\ {\text{1.46 has 2 decimal places,}} \\ {\text{and the product}} \\ {\text{4.672 has 3 decimal places.}} \end{array} \right \} 1 + 2 = 3$

Usando esta observación, podemos sugerir que la suma del número de decimales en los factores es igual al número de decimales en el producto.

$Multiplicación vertical. 1.46 veces 3.2. La primera ronda de multiplicación produce un primer producto parcial de 292. La segunda ronda produce un segundo producto parcial de 438, alineado en la columna de decenas. Toma nota que 2 decimales en el primer factor y 1 decimal en el segundo factor suma a un total de tres decimales en el producto. El producto final es 4.672.$

El método de multiplicar decimales

Método de multiplicación de decimales

Para multiplicar decimales:

Multiplique los números como si fueran números enteros.
Encuentra la suma del número de decimales en los factores.
El número de decimales en el producto es la suma que se encuentra en el paso 2.

Conjunto de Muestras A

Encuentra los siguientes productos.

$6.5 \cdot 4.3$

Solución

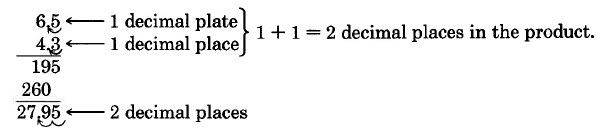
$Multiplicación vertical. 6.5 veces 4.3. La primera ronda de multiplicación produce un primer producto parcial de 195. La segunda ronda produce un segundo producto parcial de 260, alineado en la columna de decenas. Toma nota que 1 decimal en el primer factor y 1 decimal en el segundo factor suma a un total de dos decimales en el producto. El producto final es 27.95.$

Por lo tanto,$6.5 \cdot 4.3 = 27.95.$

Conjunto de Muestras A

$23.4 \cdot 1.96$

Solución

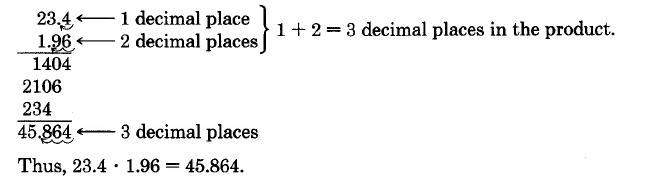
$Multiplicación vertical. 23.4 veces 1.96. La primera ronda de multiplicación produce un primer producto parcial de 1404. La segunda ronda produce un segundo producto parcial de 2106, alineado en la columna de decenas. La tercera ronda produce un tercer producto parcial de 234, alineado en la columna cien. Toma nota que 1 decimal en el primer factor y 2 decimales en el segundo factor suma a un total de tres decimales en el producto. El producto final es 45.864.$

Por lo tanto,$23.4 \cdot 1.96 = 45.864.$

Conjunto de Muestras A

Encuentra el producto de 0.251 y 0.00113 y redondea a tres decimales.

Solución

$Multiplicación vertical. 0.251 veces 0.00113. La primera ronda de multiplicación produce un primer producto parcial de 753. La segunda ronda produce un segundo producto parcial de 251, alineado en la columna de decenas. La tercera ronda produce un tercer producto parcial de 251, alineado en la columna cien. Toma nota que 3 decimales en el primer factor y 5 decimales en el segundo factor suma a un total de ocho decimales en el producto. El producto final es 0.00028363.$

Ahora, redondeando a tres decimales, obtenemos

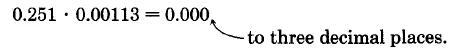
$0.251 times 0.00113 = 0.000, si el producto se redondea a tres decimales.$

Conjunto de práctica A

Encuentra los siguientes productos.

$5.3 \cdot 8.6$

Responder: 45.58

Conjunto de práctica A

$2.12 \cdot 4.9$

Responder: 10.388

Conjunto de práctica A

$1.054 \cdot 0.16$

Responder: 0.16864

Conjunto de práctica A

$0.00031 \cdot 0.002$

Responder: 0.00000062

Conjunto de práctica A

Encuentra el producto de 2.33 y 4.01 y redondea a un decimal.

Responder: 9.3

Conjunto de práctica A

$10 \cdot 5.394$

Responder: 53.94

Conjunto de práctica A

$100 \cdot 5.394$

Responder: 539.4

Conjunto de práctica A

$1000 \cdot 5.394$

Responder: 5,394

Conjunto de práctica A

$10,000 \cdot 5.394$

Contestar: 59,340

Calculadoras

Las calculadoras se pueden utilizar para encontrar productos de números decimales. Sin embargo, una calculadora que solo tiene una pantalla de ocho dígitos puede no ser capaz de manejar números o productos que dan como resultado más de ocho dígitos. Pero hay muchas calculadoras económicas ($50 - $75) con más de pantallas de ocho dígitos.

Conjunto de Muestras B

Encuentre los siguientes productos, si es posible, usando una calculadora.

$2.58 \cdot 8.61$

Solución

		Lee en pantalla
Tipo	2.58	2.58
Prensa	$\times$	2.58
Tipo	8.61	8.61
Prensa	=	22.2138

El producto es 22.2138.

Conjunto de Muestras B

$0.006 \cdot 0.0042$

Solución

		Lee en pantalla
Tipo	.006	.006
Prensa	$\times$	.006
Tipo	.0042	0.0042
Prensa	=	0.0000252

Sabemos que habrá siete decimales en el producto (ya que$3 + 4 = 7$). Dado que la pantalla muestra 7 decimales, podemos suponer que el producto es correcto. Así, el producto es 0.0000252.

Conjunto de Muestras B

$0.0026 \cdot 0.11976$

Solución

Dado que esperamos$4 + 5 = 9$ cifras decimales en el producto, sabemos que una calculadora con pantalla de ocho dígitos no podrá proporcionarnos el valor exacto. Para obtener el valor exacto, debemos usar “tecnología de mano”. Supongamos, sin embargo, que acordamos redondear este producto a tres decimales. Entonces solo necesitamos cuatro decimales en la pantalla.

		Lee en pantalla
Tipo	.0026	.0026
Prensa	$\times$	.0026
Tipo	.11976	0.11976
Prensa	=	0.0003114

Redondeando 0.0003114 a tres decimales obtenemos 0.000. Así,$0.0026 \cdot 0.11976 = 0.000$ a tres decimales.

Set de práctica B

Usa una calculadora para encontrar cada producto. Si la calculadora no proporciona el producto exacto, redondear el resultado a cuatro decimales.

$5.126 \cdot 4.08$

Contestar: 20.91408

Set de práctica B

$0.00165 \cdot 0.04$

Contestar: 0.000066

Set de práctica B

$0.5598 \cdot 0.4281$

Contestar: 0.2397

Set de práctica B

$0.000002 \cdot 0.06$

Contestar: 0.0000

Multiplicar decimales por potencias de 10

Existe una característica interesante de multiplicar decimales por potencias de 10. Considera las siguientes multiplicaciones.

Multiplicación	Número de ceros en la Potencia de 10	Número de posiciones que el punto decimal se ha movido a la derecha
$10 \cdot 8.315274 = 83.15274$	1	1
$100 \cdot 8.315274 = 831.5274$	2	2
$1,000 \cdot 8.315274 = 8,315.274$	3	3
$10,000 \cdot 8.315274 = 83,152.74$	4	4

Multiplicar un Decimal por una Potencia de 10
Para multiplicar un decimal por una potencia de 10, mueva la posición decimal a la derecha de su posición actual tantos lugares como ceros haya en la potencia de 10. Agrega ceros si es necesario.

Conjunto de Muestras C

Encuentra los siguientes productos.

$100 \cdot 34.876$. Ya que hay 2 ceros en 100, Mueve el punto decimal en 34.876 dos lugares a la derecha.

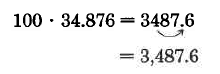
$100 veces 34.876 es igual a 3487.6. Una flecha muestra como el decimal en 34.876 se mueve dos dígitos a la derecha para hacer 3,487.6$

Conjunto de Muestras C

$1,000 \cdot 4.8058$. Ya que hay 3 ceros en 1,000, mueve el punto decimal en 4.8058 tres lugares a la derecha.

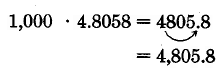
$1,000 veces 4.8058 es igual a 4805.8. Una flecha muestra como el decimal en 4.8058 se mueve tres dígitos a la derecha para hacer 4,805.8$

Conjunto de Muestras C

$10,000 \cdot 56.82$. Ya que hay 4 ceros en 10,000, mueve el punto decimal en 56.82 cuatro lugares a la derecha. Habrá que sumar dos ceros para obtener los cuatro lugares.

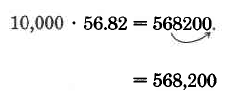
$10,000 veces 56.82 equivale a 568200. Una flecha muestra como el decimal en 56.82 se mueve cuatro dígitos a la derecha para hacer 568,200.$

Como no hay parte fraccionaria, podemos dejar caer el punto decimal.

Conjunto de Muestras C

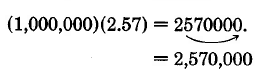
$1,000,000 veces 2.57 equivale a 2570000. Una flecha muestra como el decimal en 2.57 se mueve seis dígitos a la derecha para hacer 2,570,000.$

Conjunto de Muestras C

$1,000 veces 0.0000029 es igual a 0.0029. Una flecha muestra como el decimal en 0.0000029 se mueve seis dígitos a la derecha para hacer 0.0029.$

Set de práctica C

Encuentra los siguientes productos.

$100 \cdot 4.27$.

Contestar: 427

Set de práctica C

$10,000 \cdot 16.52187$.

Contestar: 165,218.7

Set de práctica C

$(10)(0.0188)$.

Contestar: 0.188

Set de práctica C

$(10,000,000,000)(52.7)$.

Contestar: 527,000,000,000

Multiplicación en términos de “De”

Recordando que la palabra “de” se traduce en la operación aritmética de multiplicación, observemos las siguientes multiplicaciones.

Conjunto de Muestras D

Encuentra 4.1 de 3.8.

Solución

Traduciendo “de” a "$\times$“, obtenemos

$\begin{array} {r} {4.1} \\ {\underline{\times 3.8}} \\ {328} \\ {\underline{123\ \ }} \\ {15.58} \end{array}$

Conjunto de Muestras D

Encuentra 0.95 de la suma de 2.6 y 0.8.

Solución

Primero encontramos la suma de 2.6 y 0.8.

$\begin{array} {r} {2.6} \\ {\underline{+0.8}} \\ {3.4} \end{array}$

Ahora encuentra 0.95 de 3.4

$\begin{array} {r} {3.4} \\ {\underline{\times 0.95}} \\ {170} \\ {\underline{306\ \ }} \\ {3.230} \end{array}$

Así, 0.95 de$(2.6 + 0.8)$ es 3.230.

Set de Práctica D

Encuentra 2.8 de 6.4.

Contestar: 17.92

Set de Práctica D

Encuentra 0.1 de 1.3.

Contestar: 0.13

Set de Práctica D

Encuentra 1.01 de 3.6.

Contestar: 3.636

Set de Práctica D

Encuentra 0.004 de 0.0009.

Contestar: 0.0000036

Set de Práctica D

Encuentra 0.83 de 12.

Contestar: 9.96

Set de Práctica D

Encuentra 1.1 de la suma de 8.6 y 4.2.

Contestar: 14.08

Ejercicios

Para los siguientes 30 problemas, encuentra cada producto y comprueba cada resultado con una calculadora.

Ejercicio$\PageIndex{1}$

$3.4 \cdot 9.2$

Contestar: 31.28

Ejercicio$\PageIndex{2}$

$4.5 \cdot 6.1$

Ejercicio$\PageIndex{3}$

$8.0 \cdot 5.9$

Contestar: 47.20

Ejercicio$\PageIndex{4}$

$6.1 \cdot 7$

Ejercicio$\PageIndex{5}$

$(0.1)(1.52)$

Contestar: 0.152

Ejercicio$\PageIndex{6}$

$(1.99)(0.05)$

Ejercicio$\PageIndex{7}$

$(12.52)(0.37)$

Contestar: 4.6324

Ejercicio$\PageIndex{8}$

$(5.116)(1.21)$

Ejercicio$\PageIndex{9}$

$(31.82)(0.1)$

Contestar: 3.182

Ejercicio$\PageIndex{10}$

$(16.527)(9.16)$

Ejercicio$\PageIndex{11}$

$0.0021 \cdot 0.013$

Contestar: 0.0000273

Ejercicio$\PageIndex{12}$

$1.0037 \cdot 1.00037$

Ejercicio$\PageIndex{13}$

$(1.6)(1.6)$

Contestar: 2.56

Ejercicio$\PageIndex{14}$

$(4.2)(4.2)$

Ejercicio$\PageIndex{15}$

$0.9 \cdot 0.9$

Contestar: 0.81

Ejercicio$\PageIndex{16}$

$1.11 \cdot 1.11$

Ejercicio$\PageIndex{17}$

$6.815 \cdot 4.3$

Contestar: 29.3045

Ejercicio$\PageIndex{18}$

$9.0168 \cdot 1.2$

Ejercicio$\PageIndex{19}$

$(3.5162)(0.0000003)$

Contestar: 0.00000105486

Ejercicio$\PageIndex{20}$

$(0.000001)(0.01)$

Ejercicio$\PageIndex{21}$

$(10)(4.96)$

Contestar: 49.6

Ejercicio$\PageIndex{22}$

$(10)(36.17)$

Ejercicio$\PageIndex{23}$

$10 \cdot 421.8842$

Contestar: 4,218.842

Ejercicio$\PageIndex{24}$

$10 \cdot 8.0107$

Ejercicio$\PageIndex{25}$

$100 \cdot 0.19621$

Contestar: 19.621

Ejercicio$\PageIndex{26}$

$100 \cdot 0.779$

Ejercicio$\PageIndex{27}$

$1000 \cdot 3.596168$

Contestar: 3,596.168

Ejercicio$\PageIndex{28}$

$1000 \cdot 42.7125571$

Ejercicio$\PageIndex{29}$

$1000 \cdot 25.01$

Contestar: 25.010

Ejercicio$\PageIndex{30}$

$100,000 \cdot 9.923$

Ejercicio$\PageIndex{31}$

$(4.6)(6.17)$

Producto real	Décimas	Cientos	milésimas

Contestar

Producto real	Décimas	Cientos	milésimas
28.382	28.4	28.38	28.382

Ejercicio$\PageIndex{32}$

$(8.09)(7.1)$

Producto real	Décimas	Cientos	milésimas

Ejercicio$\PageIndex{33}$

$(11.1106)(12.08)$

Producto real	Décimas	Cientos	milésimas

Contestar

Producto real	Décimas	Cientos	milésimas
134.216048	134.2	134.22	134.216

Ejercicio$\PageIndex{34}$

$0.0083 \cdot 1.090901$

Producto real	Décimas	Cientos	milésimas

Ejercicio$\PageIndex{35}$

$7 \cdot 26.518$

Producto real	Décimas	Cientos	milésimas

Contestar

Producto real	Décimas	Cientos	milésimas
185.626	185.6	185.63	185.626

Para los siguientes 15 problemas, realizar las operaciones indicadas

Ejercicio$\PageIndex{36}$

Encuentra 5.2 de 3.7.

Ejercicio$\PageIndex{37}$

Encuentra 12.03 de 10.1

Contestar: 121.503

Ejercicio$\PageIndex{38}$

Encuentra 16 de 1.04

Ejercicio$\PageIndex{39}$

Encuentra 12 de 0.1

Contestar: 1.2

Ejercicio$\PageIndex{40}$

Encuentra 0.09 de 0.003

Ejercicio$\PageIndex{41}$

Encuentra 1.02 de 0.9801

Contestar: 0.999702

Ejercicio$\PageIndex{42}$

Encuentra 0.01 de la suma de 3.6 y 12.18

Ejercicio$\PageIndex{43}$

Encuentra 0.2 de la suma de 0.194 y 1.07

Contestar: 0.2528

Ejercicio$\PageIndex{44}$

Encuentra la diferencia de 6.1 de 2.7 y 2.7 de 4.03

Ejercicio$\PageIndex{45}$

Encuentra la diferencia de 0.071 de 42 y 0.003 de 9.2

Contestar: 2.9544

Ejercicio$\PageIndex{46}$

Si una persona gana 8.55 dólares la hora, ¿cuánto gana en veinticinco centésimas de hora?

Ejercicio$\PageIndex{47}$

Un hombre compra 14 artículos a $1.16 cada uno. ¿Cuál es el costo total?

Contestar: $16.24

Ejercicio$\PageIndex{48}$

En el problema anterior, ¿cuánto es el costo total si se agrega 0.065 impuesto a las ventas?

Ejercicio$\PageIndex{49}$

Se supone que un viaje de rafting en el río durará 10 días y cada día se deben balear 6 millas. Al tercer día una persona cae de la balsa después$\dfrac{2}{5}$ de sólo el kilometraje de ese día. Si esta persona se desalienta y se retira, ¿qué fracción de todo el viaje completó?

Contestar: 0.24

Ejercicio$\PageIndex{50}$

Una mujer inicia el día con 42.28 dólares. Ella compra un artículo por 8.95 dólares y otro por $6.68. Después compra otro artículo por sesenta y dos centésimas de la cantidad restante. ¿Cuánto dinero le queda?

Problemas de la calculadora
Para los siguientes 10 problemas, utilice una calculadora para determinar cada producto. Si la calculadora no proporciona el producto exacto, redondear los resultados a cinco decimales.

Ejercicio$\PageIndex{51}$

$0.019 \cdot 0.321$

Contestar: 0.006099

Ejercicio$\PageIndex{52}$

$0.261 \cdot 1.96$

Ejercicio$\PageIndex{53}$

$4.826 \cdot 4.827$

Contestar: 23.295102

Ejercicio$\PageIndex{54}$

$(9.46)^2$

Ejercicio$\PageIndex{55}$

$(0.012)^2$

Contestar: 0.000144

Ejercicio$\PageIndex{56}$

$0.00037 \cdot 0.0065$

Ejercicio$\PageIndex{57}$

$0.002 \cdot 0.0009$

Contestar: 0.0000018

Ejercicio$\PageIndex{58}$

$0.1286 \cdot 0.7699$

Ejercicio$\PageIndex{59}$

$0.01 \cdot 0.00000471$

Contestar: 0.0000000471

Ejercicio$\PageIndex{60}$

$0.00198709 \cdot 0.03$

Ejercicios para la revisión

Ejercicio$\PageIndex{61}$

Encuentra el valor, si existe, de$0 \div 15$.

Contestar: 0

Ejercicio$\PageIndex{62}$

Encuentra el mayor factor común de 210, 231 y 357.

Ejercicio$\PageIndex{63}$

Reducir$\dfrac{280}{2,156}$ a los términos más bajos.

Contestar: $\dfrac{10}{77}$

Ejercicio$\PageIndex{64}$

Escribe “catorce ciento veintiuno diez milésimas, usando dígitos”.

Ejercicio$\PageIndex{65}$

Restar 6.882 de 8.661 y redondear el resultado a dos decimales.

Contestar: 1.78

Multiplicación	Número de ceros en la Potencia de 10	Número de posiciones que el punto decimal se ha movido a la derecha
\(10 \cdot 8.315274 = 83.15274\)	1	1
\(100 \cdot 8.315274 = 831.5274\)	2	2
\(1,000 \cdot 8.315274 = 8,315.274\)	3	3
\(10,000 \cdot 8.315274 = 83,152.74\)	4	4

Search

Text Color

Text Size

Margin Size

Font Type