9.6: División de Decimales

Last updated
Save as PDF

Page ID: 127643

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

entender el método utilizado para dividir decimales
ser capaz de dividir un número decimal por un número entero distinto de cero y por otro número decimal distinto de cero
ser capaz de simplificar una división de un decimal por una potencia de 10

La lógica detrás del método

Como hemos hecho con suma, resta y multiplicación de decimales, estudiaremos un método de división de decimales convirtiéndolos en fracciones, luego haremos una regla general.

Procederemos usando este ejemplo: Divide 196.8 por 6.

$\begin{array} {r} {32\ \ \ } \\ {6\overline{)196.8}} \\ {\underline{18\ \ \ \ \ }} \\ {16\ \ \ } \\ {\underline{12\ \ \ }} \\ {4\ \ \ } \end{array}$

Tenemos, hasta este punto, dividido 196.8 por 6 y hemos conseguido un cociente de 32 con un resto de 4. Si seguimos nuestra intuición y bajamos el .8, tenemos la división$4.8 \div 6$.

$\begin{array} {rcl} {4.8 \div 6} & = & {4 \dfrac{8}{10} \div 6} \\ {} & = & {\dfrac{48}{10} \div \dfrac{6}{1}} \\ {} & = & {\dfrac{\begin{array} {c} {^8} \\ {\cancel{48}} \end{array}}{10} \cdot \dfrac{1}{\begin{array} {c} {\cancel{6}} \\ {^1} \end{array}}} \\ {} & = & {\dfrac{8}{10}} \end{array}$

Por lo tanto,$4.8 \div 6 = .8$.

Ahora, nuestra intuición y experiencia con la división nos dirigen a colocar el .8 inmediatamente a la derecha del 32.

$División larga. 196.8 dividido por 6. 6 entra en 19 3 tiempos, con un resto de 1. Baje el 6. 6 entra en 16 dos veces, con un resto de 4. Baje el 8, y el decimal con él. 6 entra en 48 8 veces, con un resto de cero. El cociente es 32.8 Observe que los puntos decimales aparecen en la misma columna.$

A partir de estas observaciones, sugerimos el siguiente método de división.

Un método para dividir un decimal por un número entero distinto de cero

Método de dividir un decimal por un número entero distinto de cero
Para dividir un decimal por un número entero distinto de cero:

Escriba un punto decimal por encima de la línea de división y directamente sobre el punto decimal del dividendo.
Proceder a dividir como si ambos números fueran números enteros.
Si, en el cociente, el primer dígito distinto de cero ocurre a la derecha del punto decimal, pero no en la posición décimas, coloque un cero en cada posición entre el punto decimal y el primer dígito distinto de cero del cociente.

Conjunto de Muestras A

Encuentra las representaciones decimales de los siguientes cocientes.

$114.1 \div 7 = 7$

Solución

$\begin{array} {r} {16.3} \\ {7 \overline{)114.1}} \\ {\underline{7\ \ \ \ \ }} \\ {44\ \ \ } \\ {\underline{42\ \ \ }} \\ {2.1} \\ {\underline{2.1}} \\ {0} \end{array}$

Por lo tanto,$114.1 \div 7 = 16.3$

Comprobar: Si$114.1 \div 7 = 16.3$, entonces$7 \cdot 16.3$ debería ser igual a 114.1.

$\begin{array} {r} {^{4.2\ \ \ }} \\ {16.3} \\ {\underline{\ \ \ \ \ \ \ 7}} \\ {114.1} \end{array}$Cierto.

Conjunto de Muestras A

$0.02068 \div 4$

Solución

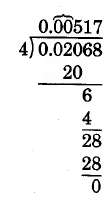
$División larga. 0.02068 dividido por 4. 4 entra en 20 5 tiempos, sin resto. 4 va a 6 una vez, con un resto de 2. Baje el 8. 4 entra en 28 7 veces, con un resto de cero. El cociente es 0.00517.$

Colocar ceros en las posiciones décimas y centésimas. (Ver Paso 3.)

Por lo tanto,$0.02068 \div 4 = 0.00517$.

Conjunto de práctica A

Encuentra los siguientes cocientes.

$184.5 \div 3$

Contestar: 61.5

Conjunto de práctica A

$16.956 \div 9$

Contestar: 1.884

Conjunto de práctica A

$0.2964 \div 4$

Contestar: 0.0741

Conjunto de práctica A

$0.000496 \div 8$

Contestar: 0.000062

Un método para dividir un decimal por un decimal distinto de cero

Ahora que podemos dividir decimales por números enteros distintos de cero, estamos en condiciones de dividir decimales por un decimal distinto de cero. Lo haremos convirtiendo una división por decimal en una división por un número entero, proceso con el que ya estamos familiarizados. Ilustraremos el método usando este ejemplo: Divide 4.32 por 1.8.

Veamos este problema como$4 \dfrac{32}{100} \div 1 \dfrac{8}{10}$.

$\begin{array} {4 \dfrac{32}{100} \div 1 \dfrac{8}{10}} & = & {\dfrac{4 \dfrac{32}{100}}{1 \dfrac{8}{10}}} \\ {} & = & {\dfrac{\dfrac{432}{100}}{\dfrac{18}{10}}} \end{array}$

El divisor es$\dfrac{18}{10}$. Podemos$\dfrac{18}{10}$ convertir en un número entero si lo multiplicamos por 10.

$\dfrac{18}{10} \cdot 10 = \dfrac{18}{\begin{array} {c} {\cancel{10}} \\ {^1} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{10}} \end{array}}{1} = 18$

Pero, sabemos por nuestra experiencia con las fracciones, que si multiplicamos el denominador de una fracción por un número entero distinto de cero, debemos multiplicar el numerador por ese mismo número entero distinto de cero. Así, al convertir$\dfrac{18}{10}$ a un número entero multiplicándolo por 10, también debemos multiplicar el numerador$\dfrac{432}{100}$ por 10.

$\begin{array} {rcl} {\dfrac{432}{100} \cdot 10 = \dfrac{432}{\begin{array} {c} {\cancel{100}} \\ {^{10}} \end{array}} \cdot \dfrac{\begin{array} {c} {^1} \\ {\cancel{10}} \end{array}}{1}} & = & {\dfrac{432 \cdot 1}{10 \cdot 1} = \dfrac{432}{10}} \\ {} & = & {43 \dfrac{2}{10}} \\ {} & = & {43.2} \end{array}$

Hemos convertido la división$4.32 \div 1.8$ en la división$43.2 \div 18$, es decir,

$1.8\overline{)4.32} \to 18 \overline{)43.2}$

Observe lo ocurrido.

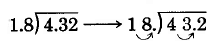
$4.32 dividido por 1.8. El lugar decimal en ambos números se mueve hacia la derecha en un espacio.$

Si “movemos” el punto decimal del divisor un dígito a la derecha, también debemos “mover” el punto decimal del dividendo un lugar a la derecha. La palabra “mover” en realidad indica el proceso de multiplicación por una potencia de 10.

Método de dividir un decimal por un número decimal Para dividir un decimal por un decimal distinto de cero,

Convierte el divisor a un número entero moviendo el punto decimal a la posición inmediatamente a la derecha del último dígito del divisor.
Mueve el punto decimal del dividendo a la derecha el mismo número de dígitos que se movió en el divisor.
Establezca el punto decimal en el cociente colocando un punto decimal directamente encima del punto decimal recién ubicado en el dividendo.
Dividir como de costumbre.

Conjunto de Muestras B

Encuentra los siguientes cocientes.

$32.66 \div 7.1$

Solución

$7.1 \underline{)32.66}$

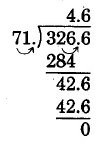
$División larga. 32.66 dividido por 7.1. Mueve el decimal a la derecha para ambos números, haciendo 326.6 dividido por 71. 71 entra en 326 4 veces, con un resto de 42. Baje el 6. 71 entra en 426 6 veces, con un resto de cero. El cociente es 4.6$

El divisor tiene una posición decimal.
Mueve el punto decimal tanto del divisor como del dividendo 1 lugar a la derecha.
Establezca el punto decimal.
Dividir como de costumbre.

Por lo tanto,$32.66 \div 7.1 = 4.6$

Comprobar:$32.66 \div 7.1 = 4.6$ si$4.6 \times 7.1 = 32.66$

$\begin{array} {c} {4.6} \\ {\underline{\times 7.1}} \\ {46} \\ {\underline{322\ \ }} \\ {32.66} \end{array}$Cierto.

Conjunto de Muestras B

$1.0773 \div 0.513$

Solución

$7.1 \underline{)32.66}$

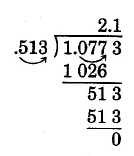
$División larga. 1.0773 dividido por .513. Mueve el decimal tres espacios a la derecha. 513 entra en 1077 dos veces, con un resto de 51. Baje el 3. 513 entra en 513 exactamente una vez. El cociente es 2.1.$

El divisor tiene 3 decimales.
Mueve el punto decimal tanto del divisor como del dividendo 3 lugares a la derecha.
Establezca la posición decimal y divida.

Por lo tanto,$1.0773 \div 0.513 = 2.1$

Comprobando multiplicando 2.1 y 0.513 nos convencerá de que hemos obtenido el resultado correcto. (Pruébalo.)

Conjunto de Muestras B

$12 \div 0.00032$

Solución

$0.00032 \underline{)12.00000}$

El divisor tiene 5 decimales.
Mueve el punto decimal tanto del divisor como del dividendo 5 lugares a la derecha. Habrá que sumar 5 ceros a 12.
Establezca la posición decimal y divida.

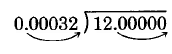
$12 dividido por 0.00032. El lugar decimal necesita moverse cinco espacios hacia la derecha, lo que significa que se deben sumar cinco ceros a la derecha de los 12 para realizar la resta.$

el suyo es ahora lo mismo que la división de números enteros.

$\begin{array} {r} {37500.} \\ {32 \overline{)1200000.}} \\ {\underline{96\ \ \ \ \ \ \ \ \ }} \\ {240\ \ \ \ \ \ \ } \\ {\underline{224\ \ \ \ \ \ \ }} \\ {160\ \ \ \ \ } \\ {\underline{160\ \ \ \ \ }} \\ {000} \end{array}$

La comprobación nos asegura eso$12 \div 0.00032 = 37,500$.

Set de práctica B

Encuentra la representación decimal de cada cociente.

$9.176 \div 3.1$

Contestar: 2.96

Set de práctica B

$5.0838 \div 1.11$

Contestar: 4.58

Set de práctica B

$16 \div 0.0004$

Contestar: 40,000

Set de práctica B

$8,162.41 \div 10$

Contestar: 816.241

Set de práctica B

$8,162.41 \div 100$

Contestar: 81.6241

Set de práctica B

$8,162.41 \div 1,000$

Contestar: 8.16241

Set de práctica B

$8,162.41 \div 10,000$

Contestar: 0.816241

Calculadoras

Las calculadoras pueden ser útiles para encontrar cocientes de números decimales. Como hemos visto con las otras operaciones de la calculadora, a veces solo podemos esperar resultados aproximados. Se nos avisa de resultados aproximados cuando la pantalla de la calculadora está llena de dígitos. Sabemos que es posible que la operación pueda producir más dígitos de los que la calculadora tiene la capacidad de mostrar. Por ejemplo, la multiplicación

$\underbrace{0.12345}_{\text{5 decimal places}} \times \underbrace{0.4567}_{\text{4 decimal places}}$

produce$5 + 4 = 9$ decimales. Una calculadora con pantalla de ocho dígitos solo tiene la capacidad de mostrar ocho dígitos, y los resultados de una aproximación. La forma de reconocer una posible aproximación se ilustra en el problema 3 del siguiente conjunto de muestras.

Conjunto de Muestras C

Encuentra cada cociente usando una calculadora. Si el resultado es una aproximación, redondea a cinco decimales.

$12.596 \div 4.7$

Solución

		Lee en pantalla
Tipo	12.596	12.596
Prensa	$\div$	12.596
Tipo	4.7	4.7
Prensa	=	2.68

Dado que la pantalla no está llena, esperamos que este sea un resultado exacto.

Conjunto de Muestras C

$0.5696376 \div 0.00123$

Solución

		Lee en pantalla
Tipo	.5696376	0.5696376
Prensa	$\div$	0.5696376
Tipo	.00123	0.00123
Prensa	=	463.12

Dado que la pantalla no está llena, esperamos que este resultado sea preciso.

Conjunto de Muestras C

$0.8215199 \div 4.113$

Solución

		Lee en pantalla
Tipo	.8215199	0.8215199
Prensa	$\div$	0.8215199
Tipo	4.113	4.113
Prensa	=	0.1997373

Hay OCHO DIGITOS — DISPLAY LLENADO ESTAR AL TANTO DE POSIBLES APROXIMACIONES.

Podemos verificar una posible aproximación de la siguiente manera. Dado que la división se$\begin{array} {r} {3\ \ \ } \\ {4 \overline{)12}} \end{array}$ puede verificar multiplicando 4 y 3, podemos verificar nuestra división realizando la multiplicación

$\underbrace{4.113}_{\text{3 decimal places}} \times \underbrace{0.1997373}_{\text{7 decimal places}}$

Esta multiplicación produce dígitos$3 + 7 = 10$ decimales. Pero nuestro cociente sospechoso contiene sólo 8 dígitos decimales. Concluimos que la respuesta es una aproximación. Entonces, redondeando a cinco decimales, obtenemos 0.19974.

Set de práctica C

Encuentra cada cociente usando una calculadora. Si el resultado es una aproximación, redondea a cuatro decimales.

$42.49778 \div 14.261$

Contestar: 2.98

Set de práctica C

$0.001455 \div 0.291$

Contestar: 0.005

Set de práctica C

$7.459085 \div 2.1192$

Contestar: 3.5197645 es un resultado aproximado. Redondeando a cuatro decimales, obtenemos 3.5198

Dividiendo decimales por potencias de 10

En los problemas 4 y 5 del Conjunto de Práctica B, encontramos las representaciones decimales de$8,162.41 \div 10$ y$8,162.41 \div 100$. Veamos cada uno de estos de nuevo y luego, a partir de estas observaciones, hagamos una declaración general respecto a la división de un número decimal por una potencia de 10.

$\begin{array} {r} {816.241} \\ {10 \overline{)8162.410}} \\ {\underline{80\ \ \ \ \ \ \ \ \ \ \ }} \\ {16\ \ \ \ \ \ \ \ \ } \\ {\underline{10\ \ \ \ \ \ \ \ \ }} \\ {62 \ \ \ \ \ \ \ } \\ {\underline{60\ \ \ \ \ \ \ }} \\ {24\ \ \ \ \ } \\ {\underline{20\ \ \ \ \ }} \\ {41\ \ \ } \\ {\underline{40\ \ \ }} \\ {10\ } \\ {\underline{10\ }} \\ {0\ } \end{array}$

Por lo tanto,$8,162.41 \div 10 = 816.241$

Observe que el divisor 10 está compuesto por uno 0 y que el cociente 816.241 se puede obtener del dividendo 8,162.41 moviendo el punto decimal un lugar a la izquierda.

$\begin{array} {r} {81.6241} \\ {100 \overline{)8162.4100}} \\ {\underline{800\ \ \ \ \ \ \ \ \ \ \ }} \\ {162\ \ \ \ \ \ \ \ \ } \\ {\underline{100\ \ \ \ \ \ \ \ \ }} \\ {624 \ \ \ \ \ \ \ } \\ {\underline{600\ \ \ \ \ \ \ }} \\ {241\ \ \ \ \ } \\ {\underline{200\ \ \ \ \ }} \\ {410\ \ \ } \\ {\underline{400\ \ \ }} \\ {100\ } \\ {\underline{100\ }} \\ {0\ } \end{array}$

Por lo tanto,$8,162.41 \div 100 = 81.6241$.

Observe que el divisor 100 está compuesto por dos 0's y que el cociente 81.6241 se puede obtener del dividendo moviendo el punto decimal dos lugares hacia la izquierda.

Usando estas observaciones, podemos sugerir el siguiente método para dividir los números decimales por potencias de 10.

Dividir una Fracción Decimal por una Potencia de 10
Para dividir una fracción decimal por una potencia de 10, mueva el punto decimal de la fracción decimal hacia la izquierda tantos lugares como ceros haya en la potencia de 10. Agrega ceros si es necesario.

Conjunto de Muestras D

Encuentra cada cociente.

$9,248.6 \div 100$

Solución

Ya que hay 2 ceros en esta potencia de 10, movemos el punto decimal 2 lugares hacia la izquierda.

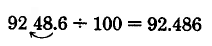
$9248.6 dividido por 100 es igual a 92.480. Observe que el único efecto es el movimiento de un decimal dos lugares a la izquierda de 9248.6.$

Conjunto de Muestras D

$3.28 \div 10,000$

Solución

Ya que hay 4 ceros en esta potencia de 10, movemos el punto decimal 4 lugares hacia la izquierda. Para ello, necesitamos sumar tres ceros.

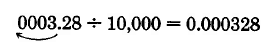
$3.28 dividido por 10,000 es igual a 0.000328. Observe que el único efecto es el movimiento de un decimal cuatro lugares a la izquierda de 0003.28.$

Set de Práctica D

Encuentra la representación decimal de cada cociente.

$182.5 \div 10$

Contestar: 18.25

Set de Práctica D

$182.5 \div 100$

Contestar: 1.825

Set de Práctica D

$182.5 \div 1,000$

Contestar: 0.1825

Set de Práctica D

$182.5 \div 10,000$

Contestar: 0.01825

Set de Práctica D

$646.18 \div 100$

Contestar: 6.4618

Set de Práctica D

$21.926 \div 1,000$

Contestar: 0.021926

Ejercicios

Para los siguientes 30 problemas, encuentra la representación decimal de cada cociente. Usa una calculadora para verificar cada resultado.

Ejercicio$\PageIndex{1}$

$4.8 \div 3$

Contestar: 1.6

Ejercicio$\PageIndex{2}$

$16.8 \div 8$

Ejercicio$\PageIndex{3}$

$18.5 \div 5$

Contestar: 3.7

Ejercicio$\PageIndex{4}$

$12.33 \div 3$

Ejercicio$\PageIndex{5}$

$54.36 \div 9$

Contestar: 6.04

Ejercicio$\PageIndex{6}$

$73.56 \div 12$

Ejercicio$\PageIndex{7}$

$159.46 \div 17$

Contestar: 9.38

Ejercicio$\PageIndex{8}$

$12.16 \div 64$

Ejercicio$\PageIndex{9}$

$37.26 \div 81$

Contestar: 0.46

Ejercicio$\PageIndex{10}$

$439.35 \div 435$

Ejercicio$\PageIndex{11}$

$36.98 \div 4.3$

Contestar: 8.6

Ejercicio$\PageIndex{12}$

$46.41 \div 9.1$

Ejercicio$\PageIndex{13}$

$3.6 \div 1.5$

Contestar: 2.4

Ejercicio$\PageIndex{14}$

$0.68 \div 1.7$

Ejercicio$\PageIndex{15}$

$60.301 \div 8.1$

Contestar: 6.21

Ejercicio$\PageIndex{16}$

$2.832 \div 0.4$

Ejercicio$\PageIndex{17}$

$4.7524 \div 2.18$

Contestar: 2.18

Ejercicio$\PageIndex{18}$

$16.2409 \div 4.03$

Ejercicio$\PageIndex{19}$

$1.002001 \div 1.001$

Contestar: 1.001

Ejercicio$\PageIndex{20}$

$25.050025 \div 5.005$

Ejercicio$\PageIndex{21}$

$12.4 \div 3.1$

Contestar: 4

Ejercicio$\PageIndex{22}$

$0.48 \div 0.08$

Ejercicio$\PageIndex{23}$

$30.24 \div 2.16$

Contestar: 14

Ejercicio$\PageIndex{24}$

$48.87 \div 0.87$

Ejercicio$\PageIndex{25}$

$12.321 \div 0.111$

Contestar: 111

Ejercicio$\PageIndex{26}$

$64,351.006 \div 10$

Ejercicio$\PageIndex{27}$

$64,351.006 \div 100$

Contestar: 643.51006

Ejercicio$\PageIndex{28}$

$64,351.006 \div 1,000$

Ejercicio$\PageIndex{29}$

$64,351.006 \div 1,000,000$

Contestar: 0.064351006

Ejercicio$\PageIndex{30}$

$0.43 \div 100$

Para los siguientes 5 problemas, encuentra cada cociente. Redondear a la posición especificada. Se puede usar una calculadora.

Ejercicio$\PageIndex{31}$

$11.2944 \div 6.24$

Cociente Real	Décimas	centésimas	milésimas

Contestar

Cociente Real	Décimas	Cientos	milésimas
1.81	1.8	1.81	1.810

Ejercicio$\PageIndex{32}$

$45.32931 \div 9.01$

Cociente Real	Décimas	centésimas	milésimas

Ejercicio$\PageIndex{33}$

$3.18186 \div 0.66$

Cociente Real	Décimas	centésimas	milésimas

Contestar

Cociente Real	Décimas	Cientos	milésimas
4.821	4.8	4.82	4.821

Ejercicio$\PageIndex{34}$

$4.3636 \div 4$

Cociente Real	Décimas	centésimas	milésimas

Ejercicio$\PageIndex{35}$

$0.00006318 \div 0.018$

Cociente Real	Décimas	centésimas	milésimas

Contestar

Cociente Real	Décimas	Cientos	milésimas
0.00351	0.0	0.00	0.004

Para los siguientes 9 problemas, encuentra cada solución.

Ejercicio$\PageIndex{36}$

Dividir el producto de 7.4 y 4.1 por 2.6.

Ejercicio$\PageIndex{37}$

Dividir el producto de 11.01 y 0.003 por 2.56 y redondear a dos decimales.

Contestar: 0.01

Ejercicio$\PageIndex{38}$

Dividir la diferencia de los productos de 2.1 y 9.3, y 4.6 y 0.8 por 0.07 y redondear a un decimal.

Ejercicio$\PageIndex{1}$

Un anillo con un costo de 567.08 dólares se pagará en pagos mensuales iguales de 46.84 dólares. ¿En cuántos meses se pagará el anillo?

Contestar: 12.11 meses

Ejercicio$\PageIndex{39}$

Seis latas de cola cuestan $2.58. ¿Cuál es el precio de una lata?

Ejercicio$\PageIndex{1}$

Una familia viajó 538,56 millas en su automóvil en un día en sus vacaciones. Si su auto usaba 19.8 galones de gasolina, ¿cuántas millas por galón obtuvo?

Contestar: 27.2 millas por galón

Ejercicio$\PageIndex{40}$

Tres estudiantes universitarios deciden rentar un departamento juntos. La renta es de $812.50 mensuales. ¿Cuánto debe aportar cada persona para la renta?

Ejercicio$\PageIndex{41}$

Una mujer nota que a baja velocidad su videograbadora recorre 296.80 unidades de cinta en 10 minutos y a velocidad rápida a través de 1098.16 unidades de cinta. ¿Cuántas veces más rápida es la velocidad rápida que la velocidad lenta?

Contestar: 3.7

Ejercicio$\PageIndex{42}$

Una clase de 34 estudiantes de primer semestre de derecho empresarial pagan un total de $1,354.90, sin tener en cuenta el impuesto a las ventas, por sus libros de texto de derecho. ¿Cuál es el costo de cada libro?

Problemas de la calculadora
Para los siguientes problemas, use la calculadora para encontrar los cocientes. Si el resultado es aproximado (ver Conjunto de Muestras C) redondea el resultado a tres decimales.

Ejercicio$\PageIndex{43}$

$3.8994 \div 2.01$

Contestar: 1.94

Ejercicio$\PageIndex{44}$

$0.067444 \div 0.052$

Ejercicio$\PageIndex{45}$

$14,115.628 \div 484.74$

Contestar: 29.120

Ejercicio$\PageIndex{46}$

$219,709.36 \div 9941.6$

Ejercicio$\PageIndex{47}$

$0.0852092 \div 0.49271$

Contestar: 0.173

Ejercicio$\PageIndex{48}$

$2.4858225 \div 1.11611$

Ejercicio$\PageIndex{49}$

$0.123432 \div 0.1111$

Contestar: 1.111

Ejercicio$\PageIndex{50}$

$2.102838 \div 1.0305$

Ejercicios para la revisión

Ejercicio$\PageIndex{51}$

Convertir$4 \dfrac{7}{8}$ a una fracción impropia.

Contestar: $\dfrac{39}{8}$

Ejercicio$\PageIndex{52}$

$\dfrac{2}{7}$de que numero es$\dfrac{4}{5}$?

Ejercicio$\PageIndex{53}$

Encuentra la suma. $\dfrac{4}{15} + \dfrac{7}{10} + \dfrac{3}{5}$.

Contestar: $\dfrac{47}{30}$o$1 \dfrac{17}{30}$

Ejercicio$\PageIndex{54}$

Redondea 0.01628 a las diez milésimas más cercanas.

Ejercicio$\PageIndex{55}$

Encuentra el producto (2.06) (1.39)

Contestar: 2.8634

Search

Text Color

Text Size

Margin Size

Font Type