9.7: Divisiones no terminadoras

Last updated
Save as PDF

Page ID: 127644

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

entender el significado de una división no terminante
ser capaz de reconocer un número no terminante por su notación

Divisiones no terminadoras

Consideremos dos divisiones:

$9.8 \div 3.5$
$4 \div 3$

Definición: Divisiones de terminación

Anteriormente, hemos considerado las divisiones como ejemplo, que es un ejemplo de una división de terminación. Una división de terminación es una división en la que el cociente termina después de varias divisiones (el resto es cero).

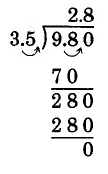
$División larga. 9.8 dividido por 3.5. El lugar decimal necesita moverse a la derecha un espacio, haciendo que el problema 98 dividido por 35. 35 va a 98 dos veces, con un resto de 28. Baje un cero para encontrar el cociente en forma decimal. 35 entra en 280 exactamente 8 veces. El cociente es 2.8$

Definición: Divisiones exactas

El cociente en este problema termina en la posición décimas. Las divisiones de terminación también se llaman divisiones exactas.

Definición: División no terminante

La división en el ejemplo es un ejemplo de una división no terminante. Una división no terminante es una división que, independientemente de lo lejos que la llevemos a cabo, siempre tiene un resto.

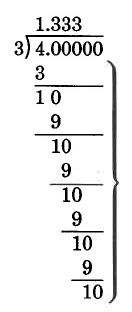
$División larga. 4 dividido por 3 equivale a 1.333, con un resto repetido sin resolver, lo que lleva a un problema de división que nunca termina.$

Definición: Decimal repetido

Podemos ver que el patrón en el corsé se repite sin cesar. Tal cociente decimal se llama decimal repetido.

Denotando cocientes no terminantes

Usamos tres puntos al final de un número para indicar que un patrón se repite sin cesar.

\[4 \div 3 = 1.333... \nonumber\]

Otra forma, además de usar tres puntos, de denotar un patrón que se repite sin cesar es escribir una barra (¯) por encima de la secuencia repetitiva de dígitos.

\[4 \div 3 = 1.\bar{3} \nonumber\]

La barra indica el patrón repetido de 3.

Los patrones repetitivos en una división se pueden descubrir de dos maneras:

A medida que avanza el proceso de división, si el resto alguna vez es el mismo que el dividendo, se puede concluir que la división no termina y que el patrón en el cociente se repite. Este hecho se ilustra en Ejemplo de Conjunto de Muestras A. A
medida que avanza el proceso de división, si el patrón de “producto, diferencia” se repite dos veces consecutivas, se puede concluir que la división es no terminante y que el patrón en el cociente se repite. Este hecho se ilustra en el Ejemplo y 4 del Conjunto de Muestras A.

Conjunto de Muestras A

Realizar cada división hasta que se pueda determinar el patrón repetitivo.

$100 \div 27$

Solución

$\begin{array} {r} {3.70370} \\ {27 \overline{)100.00000}} \\ {\underline{81\ \ \ \ \ \ \ \ \ \ \ }} \\ {19\ 0\ \ \ \ \ \ \ \ } \\ {\underline{18\ 9\ \ \ \ \ \ \ \ }} \\ {100\ \ \ \ } \\ {\underline{81\ \ \ \ }} \\ {190\ \ } \\ {189\ \ } \end{array}$

Cuando el resto es idéntico al dividendo, la división no termina. Esto implica que el patrón en el cociente se repite.

$100 \div 27 = 3.70370370...$El bloque de repetición es 703.
$100 \div 27 = 3.\overline{703}$

Conjunto de Muestras A

$1 \div 9$

Solución

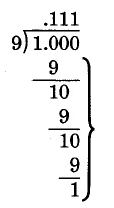
$División larga. 1 dividido por 9 un problema de división no terminante con un cociente repetido de .111$

Vemos que este patrón de “producto, diferencia” se repite. Podemos concluir que la división es no terminante y que el cociente se repite.

$1 \div 9 = 0.111...$El bloque de repetición es 1.
$1 \div 9 = 0.\overline{1}$

Conjunto de Muestras A

Divide 2 por 11 y redondea a 3 decimales.

Solución

Como deseamos redondear el cociente a tres decimales, llevaremos a cabo la división para que el cociente tenga cuatro decimales.

$\begin{array} {r} {.1818} \\ {11 \overline{)2.0000}} \\ {\underline{1.1\ \ \ \ \ \ }} \\ {90\ \ \ \ } \\ {\underline{88\ \ \ \ }} \\ {20\ \ } \\ {\underline{11\ \ }} \\ {90} \end{array}$

El número .1818 redondeado a tres decimales es .182. Así, corregir a tres decimales,

$2 \div 11 = 0.182$

Conjunto de Muestras A

Divide 1 por 6.

Solución

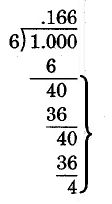
$División larga. 1 dividido por seis equivale a .166$

Vemos que este patrón de “producto, diferencia” se repite. Podemos concluir que la división es no terminante y que el cociente se repite en el 6.

$1 \div 6 = 0.16\overline{6}$

Conjunto de práctica A

Llevar a cabo las siguientes divisiones hasta que se pueda determinar el patrón repetitivo.

$1 \div 3$

Responder: $0.\overline{3}$

Conjunto de práctica A

$5 \div 6$

Responder: $0.8\overline{3}$

Conjunto de práctica A

$11 \div 9$

Responder: $1.\overline{2}$

Conjunto de práctica A

$17 \div 9$

Responder: $1.\overline{8}$

Conjunto de práctica A

Divide 7 por 6 y redondea a 2 decimales.

Responder: 1.17

Conjunto de práctica A

Divide 400 por 11 y redondea a 4 decimales.

Responder: 36.3636

Ejercicios

Para los siguientes 20 problemas, realice cada división hasta que se determine el patrón repetitivo. Si un patrón de repetición no es aparente, redondea el cociente a tres decimales.

Ejercicio$\PageIndex{1}$

$4 \div 9$

Responder: $0.\overline{4}$

Ejercicio$\PageIndex{2}$

$8 \div 11$

Ejercicio$\PageIndex{3}$

$4 \div 25$

Responder: 0.16

Ejercicio$\PageIndex{4}$

$5 \div 6$

Ejercicio$\PageIndex{5}$

$1 \div 7$

Responder: $0.\overline{142857}$

Ejercicio$\PageIndex{6}$

$3 \div 1.1$

Ejercicio$\PageIndex{7}$

$20 \div 1.9$

Responder: 10.526

Ejercicio$\PageIndex{8}$

$10 \div 2.7$

Ejercicio$\PageIndex{9}$

$1.11 \div 9.9$

Responder: $0.1\overline{12}$

Ejercicio$\PageIndex{10}$

$8.08 \div 3.1$

Ejercicio$\PageIndex{11}$

$51 \div 8.2$

Responder: $6.\overline{21951}$

Ejercicio$\PageIndex{12}$

$0.213 \div 0.31$

Ejercicio$\PageIndex{13}$

$0.009 \div 1.1$

Responder: $0.00\overline{81}$

Ejercicio$\PageIndex{14}$

$6.03 \div 1.9$

Ejercicio$\PageIndex{15}$

$0.518 \div 0.62$

Responder: 0.835

Ejercicio$\PageIndex{16}$

$1.55 \div 0.27$

Ejercicio$\PageIndex{17}$

$0.333 \div 0.999$

Responder: $0.\overline{3}$

Ejercicio$\PageIndex{18}$

$0.444 \div 0.999$

Ejercicio$\PageIndex{19}$

$0.555 \div 0.27$

Responder: $2.0\overline{5}$

Ejercicio$\PageIndex{20}$

$3.8 \div 0.99$

Problemas con la calculadora

Para los siguientes 10 problemas, utilice una calculadora para realizar cada división.

Ejercicio$\PageIndex{21}$

$7 \div 9$

Responder: $0.\overline{7}$

Ejercicio$\PageIndex{22}$

$8 \div 11$

Ejercicio$\PageIndex{23}$

$14 \div 27$

Responder: $0.\overline{518}$

Ejercicio$\PageIndex{24}$

$1 \div 44$

Ejercicio$\PageIndex{25}$

$2 \div 44$

Responder: $0.0\overline{45}$

Ejercicio$\PageIndex{26}$

$0.7 \div 0.9$(Compárelo con el ejercicio anterior)

Ejercicio$\PageIndex{27}$

$80 \div 110$(Compárelo con el ejercicio anterior)

Responder: $0.\overline{72}$

Ejercicio$\PageIndex{28}$

$0.0707 \div 0.7070$

Ejercicio$\PageIndex{29}$

$0.1414 \div 0.2020$

Responder: 0.7

Ejercicio$\PageIndex{30}$

$1 \div 0.9999999$

Ejercicio para revisión

Ejercicio$\PageIndex{31}$

En el número 411,105, ¿cuántos diez miles hay?

Responder: 1

Ejercicio$\PageIndex{32}$

Encuentra el cociente, si existe. $17 \div 0$.

Ejercicio$\PageIndex{33}$

Encuentra el mínimo común múltiplo de 45, 63 y 98.

Responder: 4410

Ejercicio$\PageIndex{34}$

Restar 8.01629 de 9.00187 y redondear el resultado a tres decimales.

Ejercicio$\PageIndex{35}$

Encuentra el cociente. $104.06 \div 12.1$.

Responder: 8.6

Search

Text Color

Text Size

Margin Size

Font Type

Ejercicio para revisión