Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

6.7: Nonterminating Divisions

Last updated

Jun 8, 2024
Save as PDF
- 6.6: Division of Decimals
- 6.8: Converting a Fraction to a Decimal

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

understand the meaning of a nonterminating division
be able to recognize a nonterminating number by its notation

Nonterminating Divisions

Let's consider two divisions:

$9.8 \div 3.5$
$4 \div 3$

Definition: Terminating Divisions

Previously, we have considered divisions like example, which is an example of a terminating division. A terminating division is a division in which the quotient terminates after several divisions (the remainder is zero).

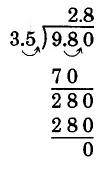
$Long division. 9.8 divided by 3.5. The decimal place needs to be moved to the right one space, making the problem 98 divided by 35. 35 goes into 98 twice, with a remainder of 28. Bring down a zero to find the quotient in decimal form. 35 goes into 280 exactly 8 times. The quotient is 2.8$

Definition: Exact Divisions

The quotient in this problem terminates in the tenths position. Terminating divisions are also called exact divisions.

Definition: Nonterminating Division

The division in example is an example of a nonterminating division. A non-terminating division is a division that, regardless of how far we carry it out, always has a remainder.

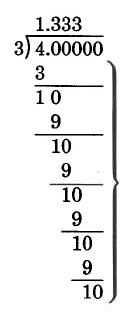
$Long division. 4 divided by 3 equals 1.333, with a repeating unresolved remainder, leading to a division problem that never terminates.$

Definition: Repeating Decimal

We can see that the pattern in the brace is repeated endlessly. Such a decimal quotient is called a repeating decimal.

Denoting Nonterminating Quotients

We use three dots at the end of a number to indicate that a pattern repeats itself endlessly.

$4 \div 3 = 1.333... \nonumber$

Another way, aside from using three dots, of denoting an endlessly repeating pattern is to write a bar ( ¯ ) above the repeating sequence of digits.

$4 \div 3 = 1.\bar{3} \nonumber$

The bar indicates the repeated pattern of 3.

Repeating patterns in a division can be discovered in two ways:

As the division process progresses, should the remainder ever be the same as the dividend, it can be concluded that the division is nonterminating and that the pattern in the quotient repeats. This fact is illustrated in Example of Sample Set A.
As the division process progresses, should the "product, difference" pattern ever repeat two consecutive times, it can be concluded that the division is nonterminating and that the pattern in the quotient repeats. This fact is illustrated in Example and 4 of Sample Set A.

Sample Set A

Carry out each division until the repeating pattern can be determined.

$100 \div 27$

Solution

$\begin{array} {r} {3.70370} \\ {27 \overline{)100.00000}} \\ {\underline{81\ \ \ \ \ \ \ \ \ \ \ }} \\ {19\ 0\ \ \ \ \ \ \ \ } \\ {\underline{18\ 9\ \ \ \ \ \ \ \ }} \\ {100\ \ \ \ } \\ {\underline{81\ \ \ \ }} \\ {190\ \ } \\ {189\ \ } \end{array}$

When the remainder is identical to the dividend, the division is nonterminating. This implies that the pattern in the quotient repeats.

$100 \div 27 = 3.70370370...$ The repeating block is 703.
$100 \div 27 = 3.\overline{703}$

Sample Set A

$1 \div 9$

Solution

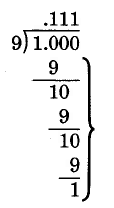
$Long division. 1 divided by 9 a nonterminating division problem with a repeating quotient of .111$

We see that this “product, difference”pattern repeats. We can conclude that the division is nonterminating and that the quotient repeats.

$1 \div 9 = 0.111...$ The repeating block is 1.
$1 \div 9 = 0.\overline{1}$

Sample Set A

Divide 2 by 11 and round to 3 decimal places.

Solution

Since we wish to round the quotient to three decimal places, we'll carry out the division so that the quotient has four decimal places.

$\begin{array} {r} {.1818} \\ {11 \overline{)2.0000}} \\ {\underline{1.1\ \ \ \ \ \ }} \\ {90\ \ \ \ } \\ {\underline{88\ \ \ \ }} \\ {20\ \ } \\ {\underline{11\ \ }} \\ {90} \end{array}$

The number .1818 rounded to three decimal places is .182. Thus, correct to three decimal places,

$2 \div 11 = 0.182$

Sample Set A

Divide 1 by 6.

Solution

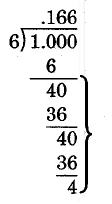
$Long division. 1 divided by six equals .166$

We see that this “product, difference” pattern repeats. We can conclude that the division is nonterminating and that the quotient repeats at the 6.

$1 \div 6 = 0.16\overline{6}$

Practice Set A

Carry out the following divisions until the repeating pattern can be determined.

$1 \div 3$

Answer: $0.\overline{3}$

Practice Set A

$5 \div 6$

Answer: $0.8\overline{3}$

Practice Set A

$11 \div 9$

Answer: $1.\overline{2}$

Practice Set A

$17 \div 9$

Answer: $1.\overline{8}$

Practice Set A

Divide 7 by 6 and round to 2 decimal places.

Answer: 1.17

Practice Set A

Divide 400 by 11 and round to 4 decimal places.

Answer: 36.3636

Exercises

For the following 20 problems, carry out each division until the repeating pattern is determined. If a repeating pattern is not apparent, round the quotient to three decimal places.

Exercise $\PageIndex{1}$

$4 \div 9$

Answer: $0.\overline{4}$

Exercise $\PageIndex{2}$

$8 \div 11$

Exercise $\PageIndex{3}$

$4 \div 25$

Answer: 0.16

Exercise $\PageIndex{4}$

$5 \div 6$

Exercise $\PageIndex{5}$

$1 \div 7$

Answer: $0.\overline{142857}$

Exercise $\PageIndex{6}$

$3 \div 1.1$

Exercise $\PageIndex{7}$

$20 \div 1.9$

Answer: 10.526

Exercise $\PageIndex{8}$

$10 \div 2.7$

Exercise $\PageIndex{9}$

$1.11 \div 9.9$

Answer: $0.1\overline{12}$

Exercise $\PageIndex{10}$

$8.08 \div 3.1$

Exercise $\PageIndex{11}$

$51 \div 8.2$

Answer: $6.\overline{21951}$

Exercise $\PageIndex{12}$

$0.213 \div 0.31$

Exercise $\PageIndex{13}$

$0.009 \div 1.1$

Answer: $0.00\overline{81}$

Exercise $\PageIndex{14}$

$6.03 \div 1.9$

Exercise $\PageIndex{15}$

$0.518 \div 0.62$

Answer: 0.835

Exercise $\PageIndex{16}$

$1.55 \div 0.27$

Exercise $\PageIndex{17}$

$0.333 \div 0.999$

Answer: $0.\overline{3}$

Exercise $\PageIndex{18}$

$0.444 \div 0.999$

Exercise $\PageIndex{19}$

$0.555 \div 0.27$

Answer: $2.0\overline{5}$

Exercise $\PageIndex{20}$

$3.8 \div 0.99$

Calculator Problems

For the following 10 problems, use a calculator to perform each division.

Exercise $\PageIndex{21}$

$7 \div 9$

Answer: $0.\overline{7}$

Exercise $\PageIndex{22}$

$8 \div 11$

Exercise $\PageIndex{23}$

$14 \div 27$

Answer: $0.\overline{518}$

Exercise $\PageIndex{24}$

$1 \div 44$

Exercise $\PageIndex{25}$

$2 \div 44$

Answer: $0.0\overline{45}$

Exercise $\PageIndex{26}$

$0.7 \div 0.9$ (Compare this with Exercise above)

Exercise $\PageIndex{27}$

$80 \div 110$ (Compare this with Exercise above)

Answer: $0.\overline{72}$

Exercise $\PageIndex{28}$

$0.0707 \div 0.7070$

Exercise $\PageIndex{29}$

$0.1414 \div 0.2020$

Answer: 0.7

Exercise $\PageIndex{30}$

$1 \div 0.9999999$

Exercise for Review

Exercise $\PageIndex{31}$

In the number 411,105, how many ten thousands are there?

Answer: 1

Exercise $\PageIndex{32}$

Find the quotient, if it exists. $17 \div 0$ .

Exercise $\PageIndex{33}$

Find the least common multiple of 45, 63, and 98.

Answer: 4410

Exercise $\PageIndex{34}$

Subtract 8.01629 from 9.00187 and round the result to three decimal places.

Exercise $\PageIndex{35}$

Find the quotient. $104.06 \div 12.1$ .

Answer: 8.6

Learning Objectives

Nonterminating Divisions

Definition: Terminating Divisions

Definition: Exact Divisions

Definition: Nonterminating Division

Definition: Repeating Decimal

Denoting Nonterminating Quotients

Sample Set A

Sample Set A

Sample Set A

Sample Set A

Exercises

Calculator Problems

Exercise for Review

Support Center

How can we help?