11.4: Solving Equations of the Form ax = b and x/a = b

Learning Objectives

• be familiar with the multiplication/division property of equality
• be able to solve equations of the form and
• be able to use combined techniques to solve equations

Multiplication/ Division Property of Equality

Recall that the equal sign of an equation indicates that the number represented by the expression on the left side is the same as the number represented by the expression on the right side. From this, we can suggest the multiplication/division property of equality.

Multiplication/Division Property of Equality
Given any equation,

1. We can obtain an equivalent equation by multiplying both sides of the equa­tion by the same nonzero number, that is, if . then is equivalent to
   
2. We can obtain an equivalent equation by dividing both sides of the equation by the same nonzero number, that is, if , then is equivalent to
   

The multiplication/division property of equality can be used to undo an association with a number that multiplies or divides the variable.

Sample Set A

Use the multiplication / division property of equality to solve each equation.

Solution

6 is associated with y by multiplication. Undo the association by dividing both sides by 6

Check: When

becomes

a true statement.

The solution to is .

Sample Set A

.

Solution

-2 is associated with by division. Undo the association by multiplying both sides by -2.

Check: When .

becomes

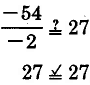
a true statement.

The solution to is

Sample Set A

.

Solution

We will examine two methods for solving equations such as this one.

Method 1: Use of dividing out common factors.

7 is associated with by division. Undo the association by multiplying both sides by 7.

Divide out the 7's

3 is associated with by multiplication. Undo the association by dviding both sides by 3.

Check: When .

becomes

a true statement.

The solution to is .

Method 2: Use of reciprocals

Recall that if the product of two numbers is 1, the numbers are reciprocals. Thus and are reciprocals.

Multiply both sides of the equation by , the reciprocal of .

Notice that we get the same solution using either method.

Sample Set A

.

Solution

-8 is associated with by multiplication. Undo the association by dividing both sides by -8.

Check: When .

becomes

a true statement.

Sample Set A

.

Solution

Since is actually and . We can isolate by multiplying both sides of the equation by -1.

.

Check: When .

becomes

The solution to is .

Practice Set A

Use the multiplication/division property of equality to solve each equation. Be sure to check each solution.

Answer

Practice Set A

Answer

Practice Set A

Answer

Practice Set A

Answer

Practice Set A

Answer

Practice Set A

Answer

Combining Techniques in Equation Solving

Having examined solving equations using the addition/subtraction and the multi­plication/division principles of equality, we can combine these techniques to solve more complicated equations.

When beginning to solve an equation such as , it is helpful to know which property of equality to use first, addition/subtraction or multiplication/di­vision. Recalling that in equation solving we are trying to isolate the variable (disas­sociate numbers from it), it is helpful to note the following.

To associate numbers and letters, we use the order of operations.

1. Multiply/divide
2. Add/subtract

To undo an association between numbers and letters, we use the order of opera­tions in reverse.

1. Add/subtract
2. Multiply/divide

Sample Set B

Solve each equation. (In these example problems, we will not show the checks.)

Solution

-4 is associated with xx by subtraction. Undo the association by adding 4 to both sides.

6 is associated with by multiplication. Undo the association by dividing both sides by 6

Sample Set B

Solution

3 is associated with by addition. Undo the association by subtracting 3 from both sides.

-8 is associated with by multiplication. Undo the association by dividing both sides by -8.

Sample Set B

.

Solution

Begin by solving this equation by combining like terms.

Choose a side on which to isolate m. Since 7 is greater than 1, we'll isolate m on the right side.
Subtract m from both sides.

8 is associated with m by subtraction. Undo the association by adding 8 to both sides.

6 is associated with m by multiplication. Undo the association by dividing both sides by 6.

Reduce,

Notice that if we had chosen to isolate m on the left side of the equation rather than the right side, we would have proceeded as follows:

Subtract from both sides.

Add 6 to both sides,

Divide both sides by -6.

This is the same result as with the previous approach.

Sample Set B

Solution

7 is associated with by division. Undo the association by multiplying both sides by 7.

8 is associated with by multiplication. Undo the association by dividing both sides by 8.

Practice Set B

Solve each equation. Be sure to check each solution.

Answer

Practice Set B

Answer

Practice Set B

Answer

Practice Set B

Answer

Practice Set B

Answer

Practice Set B

Answer

Exercises

Solve each equation. Be sure to check each result.

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

or

Exercise

Exercise

Answer

\(a = -\dfrac{5}{4})

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercise

Answer

Exercise

Exercises for Review

Exercise

Use the distributive property to compute

Answer

Exercise

Approximating by 3.14, find the approximate circumference of the circle.

Exercise

Find the area of the parallelogram.

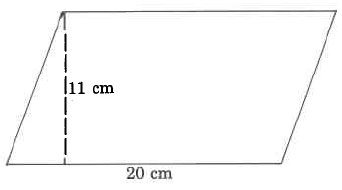
Answer

220 sq cm

Exercise

Find the value of

Exercise

Solve the equation .

Answer