8.3: Mental Arithmetic—Using the Distributive Property

Last updated
Save as PDF

Page ID: 48880

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Learning Objectives

understand the distributive property
be able to obtain the exact result of a multiplication using the distributive property

The Distributive Property

Distributive Property
The distributive property is a characteristic of numbers that involves both addition and multiplication. It is used often in algebra, and we can use it now to obtain exact results for a multiplication.

Suppose we wish to compute $3(2 + 5)$. We can proceed in either of two ways, one way which is known to us already (the order of operations), and a new way (the distributive property).

Compute $3(2 + 5)$ using the order of operations.
$3(2 + 5)$
Operate inside the parentheses first: $2 + 5 = 7$.
$3(2 + 5) = 3 \cdot 7$
Now multiply 3 and 7.
$3(2 + 5) = 3 \cdot 7 = 21$
Thus, $3(2 + 5) = 21$.
Compute $3(2 + 5)$ using the distribution property.
We know that multiplication describes repeated addition. Thus,
$\begin{array} {rclc} {3(2 + 5)} & = & {\underbrace{2 + 5 + 2 + 5 + 2 + 5}_{\text{2 + 5 appears 3 times}}} & {} \\ {} & = & {2 + 2 + 2 + 5 + 5 + 5} & {\text{(by the commutative property of addition)}} \\ {} & = & {3 \cdot 2 + 3 \cdot 5} & {\text{(since multiplication describes repeated addition)}} \\ {} & = & {6 + 15} & {} \\ {} & = & {21} & {} \end{array}$
Thus, $3(2 + 5) = 21$.
Let's look again at this use of the distributive property.
$3(2 + 5) = \underbrace{2 + 5 + 2 + 5 + 2 + 5}_{2 + 5 appears 3 times}$
$3(2 + 5) = \underbrace{2 + 2 + 2}_{2 appears 3 times} + \underbrace{5 + 5 + 5}_{5 appears 3 times}$
$3 times the quantity two plus five. Arrows point from the three to both the two and the five. This is equal to three times two plus three times five.$
The 3 has been distributed to the 2 and 5.

This is the distributive property. We distribute the factor to each addend in the parentheses. The distributive property works for both sums and differences.

Sample Set A

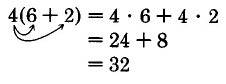
$4 times the quantity 6 plus 2. Arrows point from the 4 to both the 6 and the 2. This is equal to 4 times 6 plus 4 times 2. This is equal to 24 plus 8, which is equal to 32.$

Using the order of operations, we get

$\begin{array} {rcl} {4(6 + 2)} & = & {4 \cdot 8} \\ {} & = & {32} \end{array}$

Sample Set A

$8 times the quantity 9 plus 6. Arrows point from the 8 to both the 9 and the 6. This is equal to 8 times 9 plus 8 times 6. This is equal to 72 plus 48, which is equal to 120.$

Using the order of operations, we get

$\begin{array} {rcl} {8(9 + 6)} & = & {8 \cdot 15} \\ {} & = & {120} \end{array}$

Sample Set A

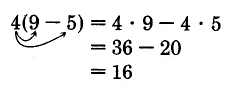
$4 times the quantity 9 minus 5. Arrows point from the 4 to both the 9 and the 5. This is equal to 4 times 9 minus 4 times 5. This is equal to 36 minus 20, which is equal to 16.$

Sample Set A

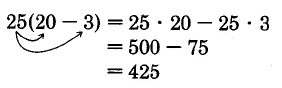
$25 times the quantity 20 minus 3. Arrows point from the 20 to both the 20 and the 3. This is equal to 25 times 20 minus 25 times 3. This is equal to 500 minus 76, which is equal to 425.$

Practice Set A

Use the distributive property to compute each value.

$6(8 + 4)$

Answer: $6 \cdot 8 + 6 \cdot 4 = 48 + 24 = 72$

Practice Set A

$4(4 + 7)$

Answer: $4 \cdot 4 + 4 \cdot 7 = 16 + 28 = 44$

Practice Set A

$8(2 + 9)$

Answer: $8 \cdot 2 + 8 \cdot 9 = 16 + 72 = 88$

Practice Set A

$12(10 + 3)$

Answer: $12 \cdot 10 + 12 \cdot 3 = 120 + 36 = 156$

Practice Set A

$6(11 - 3)$

Answer: $6 \cdot 11 - 6 \cdot 3 = 66 - 18 = 48$

Practice Set A

$8(9 - 7)$

Answer: $8 \cdot 9 - 8 \cdot 7 = 72 - 56 = 16$

Practice Set A

$15(30 - 8)$

Answer: $15 \cdot 30 - 15 \cdot 8 = 450 - 120 = 330$

Estimation Using the Distributive Property

We can use the distributive property to obtain exact results for products such as $25 \cdot 23$. The distributive property works best for products when one of the factors ends in 0 or 5. We shall restrict our attention to only such products.

Sample Set B

Use the distributive property to compute each value.

$25 \cdot 23$

Solution

Notice that $23 = 20 + 3$. We now write

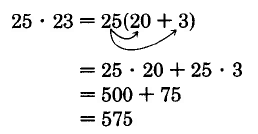
$25 times 23 equals 25 times the quantity 20 plus 3. This is equal to 25 times 20 plus 25 times 3. This is equal to 500 + 75. This is equal to 575.$

Thus, $25 \cdot 23 = 575$

We could have proceeded by writing 23 as $30 - 7$.

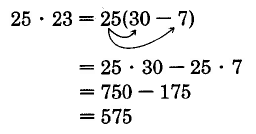
$25 times 23 equals 25 times the quantity 30 minus 7. This is equal to 25 times 30 minus 25 times 7. This is equal to 750 minus 175. This is equal to 575.$

Sample Set B

$15 \cdot 37$

Solution

Notice that $37 = 30 + 7$. We now write

$15 times 37 equals 15 times the quantity 30 plus 7. This is equal to 15 times 30 plus 15 times 7. This is equal to 450 plus 105, which is equal to 555.$

Thus, $15 \cdot 37 = 555$

We could have proceeded by writing 37 as $40 - 3$.

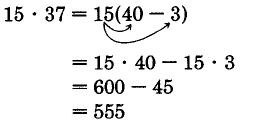
$15 times 37 equals 15 times the quantity 40 minus 3. This is equal to 15 times 40 plus 15 times 3. This is equal to 600 minus 45, which is equal to 555.$

Sample Set B

$15 \cdot 86$

Solution

Notice that $86 = 80 + 6$. We now write

$15 times 86 equals 15 times the quantity 80 plus 6. This is equal to 15 times 80 plus 15 times 6. This is equal to 1,200 plus 90, which is equal to 1,290.$

We could have proceeded by writing 86 as $90 - 4$.

$15 times 86 equals 15 times the quantity 90 minus 4. This is equal to 15 times 90 minus 15 times 4. This is equal to 1,350 minus 60, which is equal to 1,290.$

Practice Set B

Use the distributive property to compute each value.

$25 \cdot 12$

Answer: $25(10 + 2) = 25 \cdot 10 + 25 \cdot 2 = 250 + 50 = 300$

Practice Set B

$35 \cdot 14$

Answer: $35(10 + 4) = 35 \cdot 10 + 35 \cdot 4 = 350 + 140 = 490$

Practice Set B

$80 \cdot 58$

Answer: $80(50 + 8) = 80 \cdot 50 + 80 \cdot 8 = 4,000 + 640 = 4,640$

Practice Set B

$65 \cdot 62$

Answer: $65(60 + 2) = 65 \cdot 60 + 65 \cdot 2 = 3,900 + 130 = 4,030$

Exercises

Use the distributive property to compute each product.

Exercise $\PageIndex{1}$

$15 \cdot 13$

Answer: $15 (10 + 3) = 150 + 45 = 195$

Exercise $\PageIndex{2}$

$15 \cdot 14$

Exercise $\PageIndex{3}$

$25 \cdot 11$

Answer: $25 (10 + 1) = 250 + 25 = 275$

Exercise $\PageIndex{4}$

$25 \cdot 16$

Exercise $\PageIndex{5}$

$15 \cdot 16$

Answer: $15 (20 - 4) = 300 - 60 = 240$

Exercise $\PageIndex{6}$

$35 \cdot 12$

Exercise $\PageIndex{7}$

$45 \cdot 83$

Answer: $45 (80 + 3) = 3600 + 135 = 3735$

Exercise $\PageIndex{8}$

$45 \cdot 38$

Exercise $\PageIndex{9}$

$25 \cdot 38$

Answer: $25 (40 - 2) = 1,000 - 50 = 950$

Exercise $\PageIndex{10}$

$25 \cdot 96$

Exercise $\PageIndex{11}$

$75 \cdot 14$

Answer: $75 (10 + 4) = 750 + 300 = 1,050$

Exercise $\PageIndex{12}$

$85 \cdot 34$

Exercise $\PageIndex{13}$

$65 \cdot 26$

Answer: $65 (20 + 6) = 1,300 + 390 = 1,690$ or $65(30 - 4) = 1,950 - 260 = 1,690$

Exercise $\PageIndex{14}$

$55 \cdot 51$

Exercise $\PageIndex{15}$

$15 \cdot 107$

Answer: $15 (100 + 7) = 1,500 + 105 = 1,605$

Exercise $\PageIndex{16}$

$25 \cdot 208$

Exercise $\PageIndex{17}$

$35 \cdot 402$

Answer: $35 (400 + 2) = 14,000 + 70 = 14,070$

Exercise $\PageIndex{18}$

$85 \cdot 110$

Exercise $\PageIndex{19}$

$95 \cdot 12$

Answer: $95 (10 + 2) = 950 + 190 = 1,140$

Exercise $\PageIndex{20}$

$65 \cdot 40$

Exercise $\PageIndex{21}$

$80 \cdot 32$

Answer: $80 (30 + 2) = 2,400 + 160 = 2,560$

Exercise $\PageIndex{22}$

$30 \cdot 47$

Exercise $\PageIndex{23}$

$50 \cdot 63$

Answer: $50 (60 + 3) = 3,000 + 150 = 3,150$

Exercise $\PageIndex{24}$

$90 \cdot 78$

Exercise $\PageIndex{25}$

$40 \cdot 89$

Answer: $40 (90 - 1) = 3,600 - 40 = 3,560$

Exercises for Review

Exercise $\PageIndex{26}$

Find the greatest common factor of 360 and 3,780.

Exercise $\PageIndex{27}$

Reduce $\dfrac{594}{5,148}$ to lowest terms.

Answer: $\dfrac{3}{26}$

Exercise $\PageIndex{28}$

$1\dfrac{5}{9}$ of $2 \dfrac{4}{7}$ is what number?

Exercise $\PageIndex{29}$

Solve the proportion: $\dfrac{7}{15} = \dfrac{x}{90}$

Answer: $x = 42$

Exercise $\PageIndex{30}$

Use the clustering method to estimate the sum: $88 + 106 + 91 + 114$.

Search

Text Color

Text Size

Margin Size

Font Type