10.3: Absolute Value
- Page ID
- 48894
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- understand the geometric and algebraic definitions of absolute value
Geometric Definition of Absolute Value
Absolute Value-Geometric Approach
Geometric definition of absolute value:
The absolute value of a number \(a\), denoted \(|a|\), is the distance from a to 0 on the number line.
Absolute value answers the question of "how far," and not "which way." The phrase "how far" implies "length" and length is always a nonnegative quantity. Thus, the absolute value of a number is a nonnegative number.
Determine each value.
\(|4| = 4\)
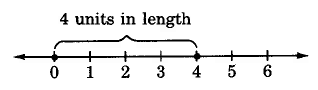
\(|-4| = 4\)
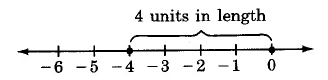
\(|0| = 0\)
\(-|5| = -5\). The quantity on the left side of the equal sign is read as "negative the absolute value of 5." The absolute value of 5 is 5. Hence, negative the absolute value of 5 is -5.
\(-|-3| = -3\). The quantity on the left side of the equal sign is read as "negative the absolute value of -3." The absolute value of -3 is 3. Hence, negative the absolute value of -3 is \(-(3) = -3\).
Practice Set A
By reasoning geometrically, determine each absolute value.
\(|7|\)
- Answer
-
7
Practice Set A
\(|-3|\)
- Answer
-
3
Practice Set A
\(|12|\)
- Answer
-
12
Practice Set A
\(|0|\)
- Answer
-
0
Practice Set A
\(-|9|\)
- Answer
-
-9
Practice Set A
\(-|-6|\)
- Answer
-
-6
Algebraic Definition of Absolute Value
From the problems in Sample Set A, we can suggest the following algebraic definition of absolute value. Note that the definition has two parts.
Absolute Value—Algebraic Approach
Algebraic definition of absolute value
The absolute value of a number a is
\(|a| = \begin{cases} a, & \text{ if } a \ge 0 \\ -a, & \text{ if } a < 0 \end{cases}\)
The algebraic definition takes into account the fact that the number aa could be either positive or zero \((a \ge 0)\) or negative \((a < 0)\).
- If the number \(a\) is positive or zero \((a \ge 0)\), the upper part of the definition applies. The upper part of the definition tells us that if the number enclosed in the absolute value bars is a nonnegative number, the absolute value of the number is the number itself.
- The lower part of the definition tells us that if the number enclosed within the absolute value bars is a negative number, the absolute value of the number is the opposite of the number. The opposite of a negative number is a positive number.
The definition says that the vertical absolute value lines may be eliminated only if we know whether the number inside is positive or negative.
Use the algebraic definition of absolute value to find the following values.
\(|8|\). The number enclosed within the absolute value bars is a nonnegative number, so the upper part of the definition applies. This part says that the absolute value of 8 is 8 itself.
\(|8| = 8\)
\(|-3|\). The number enclosed within absolute value bars is a negative number, so the lower part of the definition applies. This part says that the absolute value of -3 is the opposite of -3, which is \(-(-3)\). By the definition of absolute value and the double-negative property,
\(|-3| = -(-3) = 3\)
Practice Set B
Use the algebraic definition of absolute value to find the following values.
\(|7|\)
- Answer
-
7
Practice Set B
\(|9|\)
- Answer
-
9
Practice Set B
\(|-12|\)
- Answer
-
12
Practice Set B
\(|-5|\)
- Answer
-
5
Practice Set B
\(-|8|\)
- Answer
-
-8
Practice Set B
\(-|1|\)
- Answer
-
-1
Practice Set B
\(-|-52|\)
- Answer
-
-52
Practice Set B
\(-|-31|\)
- Answer
-
-31
Exercises
Determine each of the values.
Exercise \(\PageIndex{1}\)
\(|5|\)
- Answer
-
5
Exercise \(\PageIndex{2}\)
\(|3|\)
Exercise \(\PageIndex{3}\)
\(|6|\)
- Answer
-
6
Exercise \(\PageIndex{4}\)
\(|-9|\)
Exercise \(\PageIndex{5}\)
\(|-1|\)
- Answer
-
1
Exercise \(\PageIndex{6}\)
\(|-4|\)
Exercise \(\PageIndex{7}\)
\(-|3|\)
- Answer
-
-3
Exercise \(\PageIndex{8}\)
\(-|7|\)
Exercise \(\PageIndex{9}\)
\(-|-14|\)
- Answer
-
-14
Exercise \(\PageIndex{10}\)
\(|0|\)
Exercise \(\PageIndex{11}\)
\(|-26|\)
- Answer
-
26
Exercise \(\PageIndex{12}\)
\(-|-26|\)
Exercise \(\PageIndex{13}\)
\(-(-|4|)\)
- Answer
-
4
Exercise \(\PageIndex{14}\)
\(-(-|2|)\)
Exercise \(\PageIndex{15}\)
\(-(-|-6|)\)
- Answer
-
6
Exercise \(\PageIndex{16}\)
\(-(-|-42|)\)
Exercise \(\PageIndex{17}\)
\(|5| - |-2|\)
- Answer
-
3
Exercise \(\PageIndex{18}\)
\(|-2|^3\)
Exercise \(\PageIndex{19}\)
\(-|(2 \cdot 3)|\)
- Answer
-
6
Exercise \(\PageIndex{20}\)
\(|-2| - |-9|\)
Exercise \(\PageIndex{21}\)
\((|-6| + |4|)^2\)
- Answer
-
100
Exercise \(\PageIndex{22}\)
\((|-1| - |1|)^3\)
Exercise \(\PageIndex{23}\)
\((|4| + |-6|)^2 - (|-2|)^3\)
- Answer
-
92
Exercise \(\PageIndex{24}\)
\(-[|-10| - 6]^2\)
Exercise \(\PageIndex{25}\)
\(-\{-[-|-4| + |-3|]^3\}^2\)
- Answer
-
-1
Exercise \(\PageIndex{26}\)
A Mission Control Officer at Cape Canaveral makes the statement “lift-off, T minus 50 seconds.” How long is it before lift-off?
Exercise \(\PageIndex{27}\)
Due to a slowdown in the industry, a Silicon Valley computer company finds itself in debt $2,400,000. Use absolute value notation to describe this company’s debt.
- Answer
-
-$|-2,400,000|
Exercise \(\PageIndex{28}\)
A particular machine is set correctly if upon action its meter reads 0. One particular machine has a meter reading of -1.6 upon action. How far is this machine off its correct setting?
Exercises for Review
Exercise \(\PageIndex{29}\)
Find the sum: \(\dfrac{9}{70} + \dfrac{5}{21} + \dfrac{8}{15}\).
- Answer
-
\(\dfrac{9}{10}\)
Exercise \(\PageIndex{30}\)
Find the value of \(\dfrac{\dfrac{3}{10} + \dfrac{4}{12}}{\dfrac{19}{20}}\).
Exercise \(\PageIndex{31}\)
Convert \(3.2 \dfrac{3}{5}\) to a fraction
- Answer
-
\(3 \dfrac{13}{50}\) or \(\dfrac{163}{50}\)
Exercise \(\PageIndex{32}\)
The ratio of acid to water in a solution is \(\dfrac{3}{8}\). How many mL of acid are there in a solution that contain 112 mL of water?
Exercise \(\PageIndex{33}\)
Find the value of \(-6 - (-8)\).
- Answer
-
2


