1.1.4: Making the Moves
- Page ID
- 33488
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Lesson
Let's draw and describe translations, rotations, and reflections.
Exercise \(\PageIndex{1}\): Reflection Quick Image
Here is an incomplete image. Your teacher will display the completed image twice, for a few seconds each time. Your job is to complete the image on your copy.
Exercise \(\PageIndex{2}\): Make That Move
Your partner will describe the image of this triangle after a certain transformation. Sketch it here.
Exercise \(\PageIndex{3}\): A to B to C
Here are some figures on an isometric grid. Explore the transformation tools in the tool bar. (Directions are below the applet if you need them.)
- Name a transformation that takes Figure A to Figure B. Name a transformation that takes Figure B to Figure C.
- What is one sequence of transformations that takes Figure A to Figure C? Explain how you know.
Translate
- Select the Vector tool.

- Click on the original point and then the new point. You should see a vector.
- Select the Translate by Vector tool.

- Click on the figure to translate, and then click on the vector.
Rotate
- Select the Rotate around Point tool.

- Click on the figure to rotate, and then click on the center point.
- A dialog box will open. Type the angle by which to rotate and select the direction of rotation.
Reflect
- Select the Reflect about Line tool.

- Click on the figure to reflect, and then click on the line of reflection.
Experiment with some other ways to take Figure \(A\) to Figure \(C\). For example, can you do it with.
- No rotations?
- No reflections?
- No translations?
Summary
A move, or combination of moves, is called a transformation. When we do one or more moves in a row, we often call that a sequence of transformations. To distinguish the original figure from its image, points in the image are sometimes labeled with the same letters as the original figure, but with the symbol ' attached, as in \(A'\) (pronounced “A prime”).
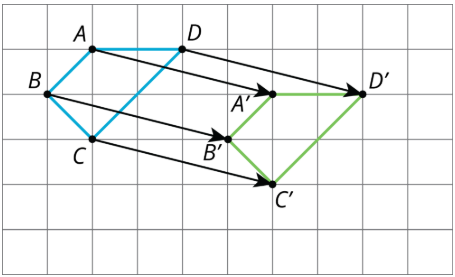
- A translation can be described by two points. If a translation moves point \(A\) to point \(A'\), it moves the entire figure the same distance and direction as the distance and direction from \(A\) to \(A'\). The distance and direction of a translation can be shown by an arrow.
For example, here is a translation of quadrilateral \(ABCD\) that moves \(A\) to \(A'\).
- A rotation can be described by an angle and a center. The direction of the angle can be clockwise or counterclockwise.
For example, hexagon \(ABCDEF\) is rotated \(90^{\circ}\) counterclockwise using center \(P\).

- A reflection can be described by a line of reflection (the “mirror”). Each point is reflected directly across the line so that it is just as far from the mirror line, but is on the opposite side.
For example, pentagon \(ABCDE\) is reflected across line \(m\).

Glossary Entries
Definition: Clockwise
An object is rotating clockwise if it is turning in the same way that the hour or minute hand goes around a clock.
The tilted square is rotated \(15^{\circ}\) clockwise from the square sitting horizontally on its base.

Definition: Corresponding
If a part of the original figure matches up with a part of the copy, we call them corresponding parts. The part could be an angle, point, or side, and you can have corresponding angles, corresponding points, or corresponding sides.
If you have a distance between two points in the original figure, then the distance between the corresponding points in the copy is called the corresponding distance.
Definition: Counterclockwise
An object is rotating counterclockwise if it is turning in the opposite way to the way that the hour or minute hand goes around a clock.
The tilted square is rotated \(15^{\circ}\) counterclockwise from the square with a horizontal base.

Definition: Image
Translations, rotations, and reflections move objects in the plane. Points, segments, and other parts of the original all have corresponding parts on the “moved object.” The moved object is called the image.
For example, here is triangle \(ABC\) and a translation to the right and up which is labeled \(DEF\).
Point \(F\) in the image corresponds to point \(C\), segment \(EF\) in the image corresponds to segment \(BD\), and angle \(DEF\) corresponds to angle \(ABC\).

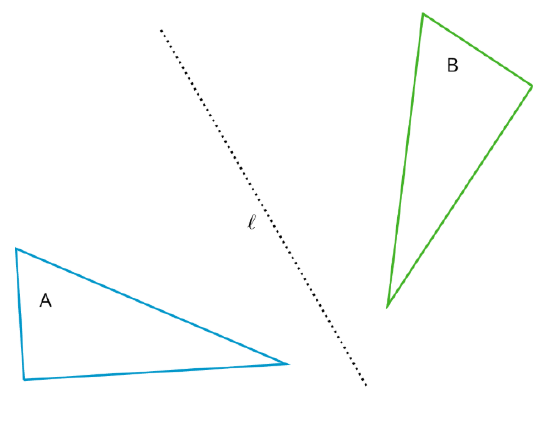
Definition: Reflection
The reflection of a figure across a line takes every point of the figure to a point directly opposite to it on the other side of the line and the same distance from the line. In the figure, the triangle \(B\) is the reflection of the triangle \(A\) across the line \(l\).
Definition: Rotation
A rotation has a center, an angle, and a direction. It moves every point of a figure in a circle around the center, in the direction specified (clockwise or counterclockwise), and for a distance specified by the angle. For example, in the figure, triangle \(A\) is rotated \(55^{\circ}\) clockwise about center \(O\) to get triangle \(B\).

Definition: Sequence of Transformations
A sequence of transformations is a set of translations, rotations, reflections, and dilations performed in a particular order on a geometric figure, resulting in a final figure.
The diagram shows a sequence of transformations consisting of a translation (from A to B) followed by a rotation (from B to C) followed by a reflection (from C to D). The last triangle is the final figure resulting from the sequence.

Definition: Transformation
A transformation is a translation, rotation, reflection, or dilation, or combination of these. There is also a more general concept of a transformation of the plane that is not discussed in grade 8.
Definition: Translation
A translation has a distance and a direction. It moves every point in a figure the given distance in the given direction.
The figure on the left is translated to the figure on the right in the direction from \(A\) to \(B\), using the distance from \(A\) to \(B\).

Practice
Exercise \(\PageIndex{4}\)
For each pair of polygons, describe a sequence of translations, rotations, and reflections that takes Polygon P to Polygon Q.
1.

2.
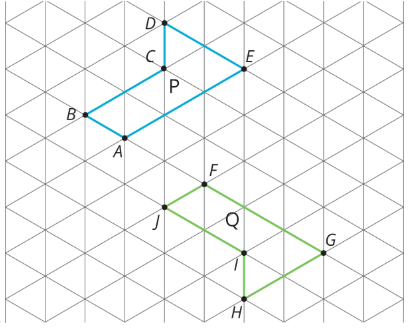
3.
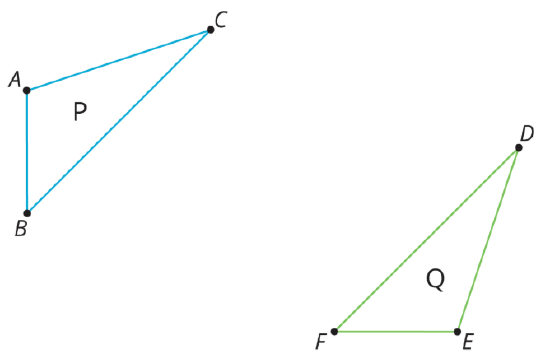
Exercise \(\PageIndex{5}\)
Here is a quadrilateral \(ABCD\) and line \(l\).

Draw the image of the quadrilateral \(ABCD\) after reflecting it across line \(l\).
(From Unit 1.1.2)
Exercise \(\PageIndex{6}\)
Here is a quadrilateral \(ABCD\).

Draw the image of quadrilateral \(ABCD\) after each rotation using \(B\) as center.
- 90 degrees clockwise
- 120 degrees clockwise
- 30 degrees counterclockwise
(From Unit 1.1.2)


