1.2.2: Rotation Patterns

Lesson

Let's rotate figures in a plane.

Exercise \(\PageIndex{1}\): Building a Quadrilateral

Here is a right isosceles triangle.

Figure \(\PageIndex{1}\)

1. Rotate triangle \(ABC\) 90 degrees clockwise around \(B\).
2. Rotate triangle \(ABC\) 180 degrees clockwise around \(B\).
3. Rotate triangle \(ABC\) 270 degrees clockwise around \(B\).
4. What would it look like when you rotate the four triangles 90 degrees clockwise around \(B\)? 180 degrees? 270 degrees clockwise?

Exercise \(\PageIndex{2}\): Rotating a Segment

Rotating a Segment

Create a segment \(AB\) and a point \(C\) that is not on segment \(AB\).

1. Rotate segment \(AB 180^{\circ}\) around point \(B\).
2. Rotate segment \(AB 180^{\circ}\) around point \(C\).

Construct the midpoint of segment \(AB\) with the Midpoint tool.

1. Rotate segment \(AB 180^{\circ}\) around its midpoint. What is the image of A?
2. What happens when you rotate a segment \(180^{\circ}\)

Are you ready for more?

Figure \(\PageIndex{2}\)

Here are two line segments. Is it possible to rotate one line segment to the other? If so, find the center of such a rotation. If not, explain why not.

Exercise \(\PageIndex{3}\): A Pattern of Four Triangles

Here is a diagram built with three different rigid transformations of triangle \(ABC\).

Use the applet to answer the questions. It may be helpful to reset the image after each question.

1. Describe a rigid transformation that takes triangle \(ABC\) to triangle \(CDE\).
2. Describe a rigid transformation that takes triangle \(ABC\) to triangle \(EFG\).
3. Describe a rigid transformation that takes triangle \(ABC\) to triangle \(GHA\).
4. Do segments \(AC\), \(CE\), \(EG\), and \(GA\) all have the same length? Explain your reasoning.

Summary

When we apply a 180-degree rotation to a line segment, there are several possible outcomes:

• The segment maps to itself (if the center of rotation is the midpoint of the segment).
• The image of the segment overlaps with the segment and lies on the same line (if the center of rotation is a point on the segment).
• The image of the segment does not overlap with the segment (if the center of rotation is not on the segment).

We can also build patterns by rotating a shape. For example, triangle \(ABC\) shown here has \(m(\angle A)=60\). If we rotate triangle \(ABC\) 60 degrees, 120 degrees, 180 degrees, 240 degrees, and 300 degrees clockwise, we can build a hexagon.

Figure \(\PageIndex{3}\): Six identical equilateral triangles are drawn such that each triangle is aligned to another triangle created a hexagon. One of the triangle is labeled A B C and all 6 triangles meet at the common point of A.

Glossary Entries

Definition: Corresponding

When part of an original figure matches up with part of a copy, we call them corresponding parts. These could be points, segments, angles, or distances.

For example, point \(B\) in the first triangle corresponds to point \(E\) in the second triangle. Segment \(AC\) corresponds to segment \(DF\).

Figure \(\PageIndex{4}\)

Definition: Rigid Transformation

A rigid transformation is a move that does not change any measurements of a figure. Translations, rotations, and reflections are rigid transformations, as is any sequence of these.

Practice

Exercise \(\PageIndex{4}\)

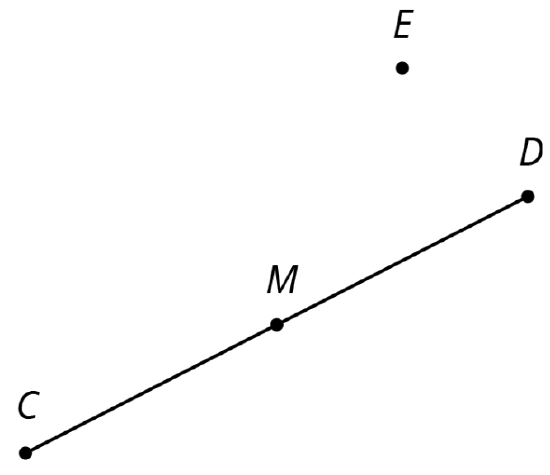
For the figure shown here,

1. Rotate segment \(CD\) \(180^{\circ}\) around point \(D\).
2. Rotate segment \(CD\) \(180^{\circ}\) around point \(E\).
3. Rotate segment \(CD\) \(180^{\circ}\) around point \(M\).

Figure \(\PageIndex{5}\)

Exercise \(\PageIndex{5}\)

Here is an isosceles right triangle:

Draw these three rotations of triangle \(ABC\) together.

1. Rotate triangle \(ABC\) 90 degrees clockwise around \(A\).
2. Rotate triangle \(ABC\) 180 degrees around \(A\).
3. Rotate triangle \(ABC\) 270 degrees clockwise around \(A\).

Figure \(\PageIndex{6}\)

Exercise \(\PageIndex{6}\)

Each graph shows two polygons \(ABCD\) and \(A'B'C'D'\). In each case, describe a sequence of transformations that takes \(ABCD\) to \(A'B'C'D'\).

1.

Figure \(\PageIndex{7}\): Quadrilateral \(ABCD\) and its image quadrilateral \(A'B'C'D'\) on a coordinate plane, origin \(O\). Horizontal axis scale negative 5 to 5 by 1’s. Vertical axis scale negative 2 to 3 by 1’s. The coordinates of \(ABCD\) are \(A\)(negative 3 comma 3), \(B\)(negative 4 comma 1), \(C\)(negative 2 comma negative 1)and \(D\)(negative 2 comma 2). The coordinates of \(A'B'C'D'\) are \(A'\)(3 comma 2), \(B'\)( 4 comma 0), \(C'\)(2 comma negative 2)and \(D'\)(2 comma 1).

2.

Figure \(\PageIndex{8}\): Quadrilateral \(ABCD\) and its image quadrilateral \(A'B'C'\) and \(D'\) on a coordinate plane, origin \(O\). Horizontal axis scale negative 5 to 7 by 1’s. Vertical axis scale negative 1 to 4 by 1’s. The coordinates of \(ABCD\) are \(A\)(negative 4 comma 1), \(B\)(negative 1 comma 0), \(C\)(1 comma 3)and \(D\)(negative 2 comma 3). The coordinates of \(A'B'C'D'\) are \(A'\)(4 comma 4), \(B'\)(3 comma 1), \(C'\)(6 comma negative 1)and \(D'\)(6 comma 2).

(From Unit 1.1.5)

Exercise \(\PageIndex{7}\)

Lin says that she can map Polygon A to Polygon B using only reflections. Do you agree with Lin? Explain your reasoning.

Figure \(\PageIndex{9}\): Two quadrilaterals polygon A and B on a grid. Let (0 comma 0) be the bottom left corner. Then the coordinates of polygon A are: (1 comma 4), (3 comma 7), (4 comma 5) and (3 comma 4). The coordinates of polygon B are: (5 comma 1), (7 comma 4), (5 comma 4) and (4 comma 3).

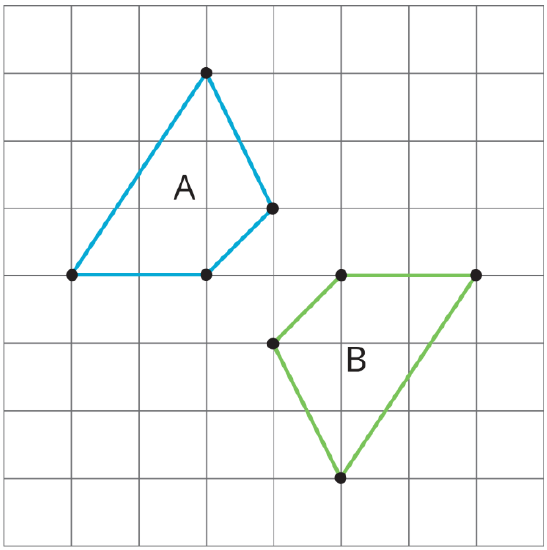
(From Unit 1.1.4)