2.1.3: Dilations with no Grid

Lesson

Let's dilate figures not on grids.

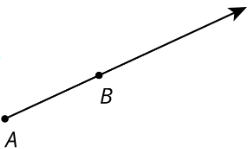
Exercise \(\PageIndex{1}\): Points on a Ray

1. Find and label a point \(C\) on the ray whose distance from \(A\) is twice the distance from \(B\) to \(A\).
2. Find and label a point \(D\) on the ray whose distance from \(A\) is half the distance from \(B\) to \(A\).

Figure \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\): Dilation Obstacle Course

1. Dilate \(B\) using a scale factor of 5 and \(A\) as the center of dilation. Which point is its image?
2. Using \(H\) as the center of dilation, dilate \(G\) so that its image is \(E\). What scale factor did you use?
3. Using \(H\) as the center of dilation, dilate \(E\) so that its image is \(G\). What scale factor did you use?
4. To dilate \(F\) so that its image is \(B\), what point on the diagram can you use as a center?
5. Dilate \(H\) using \(A\) as the center and a scale factor of \frac{1}{3}\). Which point is its image?
6. Describe a dilation that uses a labeled point as its center and that would take \(F\) to \(H\).
7. Using \(B\) as the center of dilation, dilate \(H\) so that its image is itself. What scale factor did you use?

Exercise \(\PageIndex{3}\): Getting Perspective

1. Dilate \(P\) using \(C\) as the center and a scale factor of 4. Follow the directions to perform the dilations in the applet.
   1. Select the Dilate From Point tool.
      
   2. Click on the object to dilate, and then click on the center of dilation.
   3. When the dialog box opens, enter the scale factor. Fractions can be written with plain text, ex. 1/2.
   4. Click
      
   5. Use the Ray tool and the Distance tool to verify.
2. Dilate \(Q\) using \(C\) as the center and a scale factor of \(\frac{1}{2}\).
3. Draw a simple polygon.
   1. Choose a point outside the polygon to use as the center of dilation. Label it \(C\).
   2. Using your center \(C\) and the scale factor you were given, draw the image under the dilation of each vertex of the polygon, one at a time. Connect the dilated vertices to create the dilated polygon.
   3. Draw a segment that connects each of the original vertices with its image. This will make your diagram look like a cool three-dimensional drawing of a box! If there's time, you can shade the sides of the box to make it look more realistic.
   4. Compare your drawing to other people’s drawings. What is the same and what is different? How do the choices you made affect the final drawing? Was your dilated polygon closer to \(C\) than to the original polygon, or farther away? How is that decided?

Are you ready for more?

Here is line segment \(DE\) and its image \(D'E'\) under a dilation.

Figure \(\PageIndex{2}\)

1. Use a ruler to find and draw the center of dilation. Label it \(F\).
2. What is the scale factor of the dilation?

Summary

If \(A\) is the center of dilation, how can we find which point is the dilation of \(B\) with scale factor 2?

Figure \(\PageIndex{3}\)

Since the scale factor is larger than 1, the point must be farther away from \(A\) than \(B\) is, which makes \(C\) the point we are looking for. If we measure the distance between \(A\) and \(C\), we would find that it is exactly twice the distance between \(A\) and \(B\).

A dilation with scale factor less than 1 brings points closer. The point \(D\) is the dilation of \(B\) with center \(A\) and scale factor \(\frac{1}{3}\).

Glossary Entries

Definition: Center of a Dilation

The center of a dilation is a fixed point on a plane. It is the starting point from which we measure distances in a dilation.

In this diagram, point \(P\) is the center of the dilation.

Figure \(\PageIndex{4}\)

Definition: Dilation

A dilation is a transformation in which each point on a figure moves along a line and changes its distance from a fixed point. The fixed point is the center of the dilation. All of the original distances are multiplied by the same scale factor.

For example, triangle \(DEF\) is a dilation of triangle \(ABC\). The center of dilation is \(O\) and the scale factor is 3.

This means that every point of triangle \(DEF\) is 3 times as far from \(O\) as every corresponding point of triangle \(ABC\).

Figure \(\PageIndex{5}\)

Definition: Scale Factor

To create a scaled copy, we multiply all the lengths in the original figure by the same number. This number is called the scale factor.

In this example, the scale factor is 1.5, because \(4\cdot (1.5)=6\), \(5\cdot (1.5)=7.5\), and \(6\cdot (1.5)=9\).

Figure \(\PageIndex{6}\)

Practice

Exercise \(\PageIndex{4}\)

Segment \(AB\) measures 3 cm. Point \(O\) is the center of dilation. How long is the image of \(AB\) after a dilation with ...

1. Scale factor \(5\)?
2. Scale factor \(3.7\)?
3. Scale factor \(\frac{1}{5}\)?
4. Scale factor \(s\)?

Exercise \(\PageIndex{5}\)

Here are points \(A\) and \(B\). Plot the points for each dilation described.

Figure \(\PageIndex{7}\)

1. \(C\) is the image of \(B\) using \(A\) as the center of dilation and a scale factor of \(2\).
2. \(D\) is the image of \(A\) using \(B\) as the center of dilation and a scale factor of \(2\).
3. \(E\) is the image of \(B\) using \(A\) as the center of dilation and a scale factor of \(\frac{1}{2}\).
4. \(F\) is the image of \(A\) using \(B\) as the center of dilation and a scale factor of \(\frac{1}{2}\).

Exercise \(\PageIndex{6}\)

Make a perspective drawing. Include in your work the center of dilation, the shape you dilate, and the scale factor you use.

Exercise \(\PageIndex{7}\)

Triangle \(ABC\) is a scaled copy of triangle \(DEF\). Side \(AB\) measures 12 cm and is the longest side of \(ABC\). Side \(DE\) measures 8 cm and is the longest side of \(DEF\).

1. Triangle \(ABC\) is a scaled copy of triangle \(DEF\) with what scale factor?
2. Triangle \(DEF\) is a scaled copy of triangle \(ABC\) with what scale factor?

(From Unit 2.1.1)

Exercise \(\PageIndex{8}\)

The diagram shows two intersecting lines.

Figure \(\PageIndex{8}\): Two intersecting lines, forming a X. The top angle is labeled 102 degrees. The left angle is labeled a degrees. The bottom angle is labeled b degrees. The right angle is labeled c degrees.

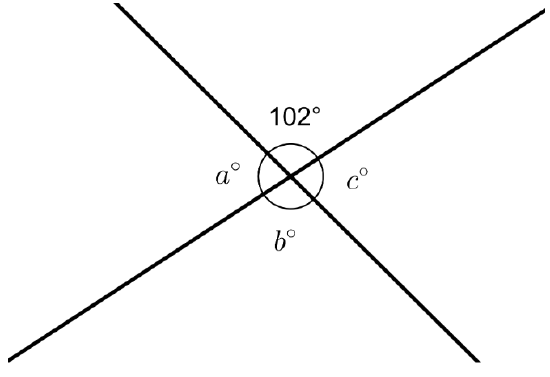
Find the missing angle measures.

(From Unit 1.4.1)

Exercise \(\PageIndex{9}\)

1. Show that the two triangles are congruent.
2. Find the side lengths of \(DEF\) and the angle measures of \(ABC\).

Figure \(\PageIndex{9}\): Two triangles in an x y plane. Origin O. Horizontal axis from negative 6 to 6, by 1s. Vertical axis from negative 4 to 4, by 1s. Triangle A B C. Point A at negative 2 comma 4. Point B at negative 6 comma 1. Point C at negative 3 comma 1. Side A C is labeled 3 point 2. Side C B is labeled 3. Side A B is labeled 5. Triangle D E F. Point D at 3 comma negative 1. Point F at 4 comma negative 4. Point E at 7 comma negative 4. Angle F E D is labeled 36 point 9 degrees. Angle E D F is labeled 34 point 7 degrees. Angle D F E is labeled 108 point 4 degrees.

(From Unit 1.2.1)